(La copertina della IV edizione, 1912, del saggio
di Richard Dedekind dedicato al problema del "continuo"
dal sito http://www-math.sci.kun.nl/werkgroepen/gmfw/bronnen/dedekind2.html)

Appendice sulle definizioni matematiche
di discreto e continuo

Nella precedente discussione dei paradossi di Zenone, abbiamo fatto innumerevoli volte ricorso, in modo essenziale, alle nozioni di discreto e continuo, senza che di esse venisse offerta una "definizione" precisa, secondo i canoni della matematica moderna. Ci è parsa quindi opportuna un'appendice che rispondesse a tale esigenza, tanto più che resterebbe sorpreso chi pensasse di rinvenire facilmente delucidazioni in proposito nella "letteratura" corrente. Colui che cercasse una siffatta definizione per il continuo, potrebbe imbattersi in osservazioni come: <<Il termine assume in campo matematico una pluralità di significati>> (Grande Dizionario Enciclopedico, UTET, 1986), seguita di solito da una serie di illustrazioni dell'annunciata polisemia, nessuna delle quali sarebbe però, secondo noi, "giusta". Per esempio, a parte i concetti di "continuità" di una funzione, o il "postulato di continuità" della retta ordinaria (di cui ci occuperemo nel par. 5), troverebbe che in topologia si dice continuo uno spazio topologico <<che sia contemporaneamente connesso e compatto>>, o che in teoria degli insiemi si dice potenza (o cardinale) del continuo quella dell'insieme dei numeri reali (in simboli: R). In aggiunta a queste due nozioni, troverebbe un trattamento algebrico della questione, che indaga le proprietà di particolari ordini compatibili con determinate strutture algebriche (teoria dei campi ordinati, specialmente il teorema di unicità di un campo ordinato completo archimedeo, punto culminante dell'approccio assiomatico-formale alla costruzione dei numeri reali), e fa intervenire una nozione, appunto l'archimedeicità, che, come vedremo, appare invece del tutto estranea all'essenza del continuo. Quasi la stessa cosa, ancorché si tratti di problema assai più semplice, per il termine "duale" discreto, che viene utilizzato in contrapposizione a continuo, ma senza che siano chiariti quanto si vorrebbe né l'uno né l'altro. Curioso riscontrare per esempio che in un intero libro intitolato Il discreto e il continuo (Willem Kuyk, Boringhieri, Torino, 1982), un'opera del resto interessante e alquanto avanzata dal punto di vista "tecnico", non è riportata alcuna delle ricercate definizioni (ci sembra, neppure quella topologica sopra menzionata, che peraltro criticheremo nel par. 8), ma solo considerazioni di taglio insiemistico, assieme a un vago (ma in ogni caso corretto) accenno del tipo: <<dopo aver formato, attraverso un complicato processo di apprendimento, i concetti di continuo (le "entità" geometriche) e di discreto (le "entità" dei numeri naturali), la mente umana gode di una grandissima libertà nell'operare con essi come "materiale base" per la costruzione di "strutture">> (p. 10)¹. Né di più rinverrebbe ne Il continuo... di Hermann Weyl (loc. cit. nell'articolo precedente, d'ora in avanti "Zenone", nota 38), nonostante il relativo capitolo II si chiami "Il concetto di numero e il continuo - Fondamenti del calcolo infinitesimale", perché vi si fa unico riferimento all'uso cantoriano di attribuire il termine continuo alla totalità dei numeri reali: quindi, occuparsi del continuo significa, da questa prospettiva, illustrare la meticolosa costruzione di tali numeri che segue.

Insomma, si tratta di merce che, ed è davvero incredibile, non è di facile reperimento, e corrispondentemente non è neppure comune oggetto di insegnamento nei corsi di matematica (che poi questa sia una causa o un effetto - o entrambi, in virtù dell'instaurarsi di un feedback attualmente niente affatto "virtuoso" - resterebbe da stabilirsi). Per quanto ne sappiamo, non ce n'è traccia negli ordinari testi di Algebra e Geometria adottati nelle università italiane nell'ultimo mezzo secolo (né tanto meno nelle lezioni di Analisi Matematica - con qualche eccezione, e in ogni caso relativa a presentazioni parziali dell'argomento, nelle più "vecchie"), né in quelli che sono stati guida nel fissare il "canone internazionale", quali il Van der Waerden (Moderne Algebra, 1931), il Birkhoff-Mac Lane (A Survey of Modern Algebra, 1941; poi Mac Lane-Birkhoff, Algebra, 1965 - ottimo sotto molti punti di vista), il Godement (Cours d'Algèbre, 1966), e ancora le opere di Nathan Jacobson, Serge Lang, etc.. C'è da domandarsi se l'assenza di attenzione verso i temi  su cui verteranno le nostre riflessioni debba indurre a farli ritenere marginali: ma è veramente legittimo qualificare tali delle questioni da sempre riconosciute alle radici più autentiche e profonde della matematica? (nei libri nominati si troverebbe invece un sacco di teoria degli insiemi, dei gruppi,...).

Come dire che la presente appendice è un esempio delle "riscoperte" che si compiono quando, ai giorni nostri, si affrontino certe tematiche con una prospettiva diversa da quella a cui intere generazioni di matematici sono state acriticamente abituate sin dai primi anni della loro formazione, che prevede una sorta di condizionamento a ripetere stancamente gli slogan che hanno caratterizzato il dibattito sui fondamenti all'inizio del '900, tra tanta apparente molteplicità di posizioni, ma in effetti un unico atteggiamento mentale, caratterizzato da una miscela - variabile, questa sì, da individuo a individuo - di scetticismo, relativismo, nichilismo, pragmatismo, tutte espressioni dell'"anti-umanesimo post-darwinista" che denunciamo sovente². Appare prova della correttezza di tale descrizione quanto ebbe a rispondermi poco tempo fa un valente collega, al quale chiedevo lumi sulle definizioni che andavo cercando: <<non so risponderti; aggiungerò che non ho mai capito cosa si debba intendere per "matematica discreta"; fra l'altro le due parole "discreto" e "continuo" vengono spesso usate come se avessero significati opposti e complementari. Proprio non so>>. [Si veda inoltre la discussione su "The notion of continuity applied to sets" che è riportata in http://www.physicsforums.com/archive/t-7501.]

(Quanto precede vale naturalmente al meglio della nostra "onesta" conoscenza. Saremo lieti di aggiornare le informazioni fornite con altre desunte da eventuali segnalazioni dei lettori, di cui daremmo notizia nel prossimo numero di Episteme.)

In effetti, come sostenuto in "Zenone", continuo e discreto sono concetti sicuramente contrapposti, che si rifanno, nell'ordine, al dualismo spazio-tempo, e quindi a quello geometria-aritmetica, e si è costretti a ritenere che solamente una deplorevole filosofia della matematica³ sia responsabile dello stato di cose dianzi descritto, con la sua pretesa di essere riuscita a <<sostituire al continuo geometrico il continuo "aritmetico">> (enfasi nel testo), così afferma, in piena conformità alla corrente vulgata, Corrado Mangione ("Logica e problema dei fondamenti nella seconda metà dell'Ottocento", in: Ludovico Geymonat, Storia del Pensiero Filososofico e Scientifico, Garzanti, Milano, 1970; nuova edizione 1976, vol. VI, p. 361). L'autore cita poi con compiacimento Bertrand Russell, quando ne I princìpi della matematica⁴ sostiene il seguente discutibilissimo punto di vista (niente a che fare con la matematica intesa quale scienza dai contenuti oggettivi, "trascendentali", e pertanto universalmente condivisibili, ossia la mathesis universalis di Cartesio, e di Leibnitz), espressione di un rozzo anti-kantismo: <<Si supponeva un tempo, e qui sta la vera forza della filosofia della matematica di Kant, che la continuità avesse un riferimento essenziale allo spazio e al tempo [...] Secondo quest'ipotesi la filosofia dello spazio e del tempo precedeva quella della continuità [...] Tutto ciò è mutato per opera dei matematici moderni. Ciò che si chiama l'aritmetizzazione della matematica ha fatto vedere che tutti i problemi presentati, a questo riguardo, dallo spazio e dal tempo, sono già presenti nell'aritmetica pura. [...] [Sicché risulta ora possibile] dare una definizione generale di continuità, senza fare appello a quella massa di pregiudizi non analizzati che i kantiani chiamano "intuizione">> (cap. XXXII). Dichiarazioni dicevamo comunemente accettate, che sono all'origine della denunciata carenza, tanto più deprecabile quanto gli elementi matematici necessari per risolvere con piena soddisfazione la questione sono tutti ben noti⁵. Nel campo della filosofia matematica, nessuno più indaga con attenzione e spirito critico i fondamenti, osando semmai fare opera "rivoluzionaria", cioè volgere indietro la prua della barca: del monumento eretto alla fine del XIX secolo e nei primi decenni del XX si esegue solo l'ordinaria manutenzione⁶.

Quella cui ci accingiamo sarà dunque principalmente un'impresa di scelta di definizioni, e di loro confronto, un'attività che riteniamo essenziale per un matematico-filosofo, a maggior ragione se "insegnante" (a proposito dell'intenzionale commistione di due categorie di studiosi, usualmente mantenute distinte, al punto che matematica e filosofia appartengono a due facoltà universitarie differenti - la prima essendo assurdamente inserita tra le scienze sperimentali, la seconda tra quelle letterarie! - rammentiamo che Gottlob Frege ebbe a dire, con molta ragione, che: <<Every good mathematician is at least half a philosopher, and every good philosopher is at least half a mathematician>>). Asseriamo ciò in accordo con l'opinione di Federigo Enriques: <<Il significato della matematica, pur considerato nel suo aspetto logico, apparirà in una luce assai diversa se, in luogo di guardare alle dimostrazioni, si guardi piuttosto alle definizioni, mercé cui si costituiscono oggetti di studio via via più elevati>> (loc. cit. nella nota 44 di "Zenone", p. 145)⁷. Aggiungeremmo che un'opportuna scelta delle definizioni permette di raccogliere, e coordinare mettendone in evidenza le relazioni, diverse verità pertinenti a una data fenomenologia matematica, che così riesce descritta in un modo armonioso, e non già come insieme di fatti isolati, di cui rimane difficile comprendere le ultime e intime ragioni.

Osserviamo che, per ovvi motivi, le pagine seguenti saranno fruite meglio da chi ha già qualche dimestichezza con il "gergo" della matematica (a mo' di riferimento indichiamo le nostre dispense di Algebra, d'ora in avanti definite semplicemente "dispense": vi si può accedere dalla pagina: http://www.dipmat.unipg.it/~bartocci/mat/alg-prog.htm). Si auspica però che la loro essenza sia alla portata di tutti, dal momento che si tratta di questioni importanti (cioè, non esclusivamente per "specialisti"), e non troppo difficili da intendere. Come dire che, nello spirito del commento di Frege sopra menzionato, bisognerebbe essere in grado di comprendere almeno il senso delle definizioni, e degli enunciati dei teoremi, o di alcuni di essi. Perciò, talune dimostrazioni sono state solo accennate (fornendo comunque, nei casi che si potevano ritenere meno banali e/o noti, ogni elemento perché sia poi possibile perfezionarle in proprio), e abbiamo segnalato con un asterisco le parti che potrebbero essere omesse in prima lettura da coloro meno familiari con certo linguaggio (i quali potrebbero omettere anche tutto ciò che si riferisce maggiormente a concetti di natura topologica, o alla complessa terminologia - ma niente di più - dell'algebra "astratta").

Avvertenza. Nonostante al complesso del presente lavoro si sia riflettuto, lo si è detto in "Zenone", per molto tempo, pure la sua redazione finale ha sofferto della cronica carenza di quest'elemento così importante nella vita di ogni essere umano, e che costituisce uno dei protagonisti "gemelli" del nostro studio. Si spera di non essere incorsi in troppe sviste, soprattutto nell'appendice, e che esse siano comunque di tipo veniale, tali cioè che la relativa correzione non debba richiedere un eccessivo lavoro di bisturi. Annunciato che un eventuale errata corrige verrà inserito nel prossimo numero della rivista, si ringraziano in anticipo quei lettori che vorranno cortesemente aiutarci nel lavoro di revisione che non si è purtroppo potuto compiere finora, come sarebbe stato invece auspicabile.

2. Insiemi, spazi ordinati e spazi topologici*

Per quanto riguarda definizioni che potremmo definire "generiche", perché non strettamente matematiche, ma in ogni caso istruttive, citiamo, oltre a quella contenuta nella nota 25 di "Zenone", il prezioso collaboratore di Episteme, Bruno d'Ausser Berrau (comunicazione privata): <<dal punto di vista della nostra percezione, un insieme fenomenico può definirsi discreto allorché la sensazione da esso trasmessaci sia scindibile in un sottoinsieme di sensazioni elementari relative ad oggetti nettamente distinguibili l'uno dall'altro. Al contrario, se per un altro insieme di fenomeni le sensazioni elementari relative alle sue parti non siano in alcun modo differenziabili, siamo alla presenza di un continuo. Il continuo ci appare nettamente associato al contiguo pel quale è continuo ciò che è composto da elementi i cui limiti si toccano e si confondono>>. Tali riflessioni fungendoci da guida, cominciamo con l'uscire nettamente da un equivoco: in matematica, l'unico ambito dove sia possibile precisarli in modo esauriente e rigoroso, i concetti di discreto e continuo non hanno a che fare (almeno preliminarmente) né con la teoria degli insiemi, né con la topologia, né con strutture algebriche, etc., bensì con la pura e semplice categoria dell'ordine⁸. Ovvero, si tratta di due attributi specificativi che possono essere associati esclusivamente a quello che diremo uno spazio ordinato, termine con cui intenderemo un insieme X dotato di una struttura d'ordine totale w , sicché uno spazio ordinato verrà indicato con il simbolo (X,w ). La relazione w permette di confrontare tra loro elementi di X, ossia di stabilire, dati due qualsiasi elementi x, y Î X (a ciò allude la specificazione "totale", altrimenti si parla di ordinamento "parziale"; il simbolo Î , detto simbolo di Peano, si legge: "elemento di"), quale dei due precede l'altro, ciò che in simboli verrà specificato con la scrittura x £ y, dove il riferimento ad w viene addirittura omesso (ovviamente, quando non vi sia luogo ad equivoci)⁹. Il simbolo x < y starà a significare che x £ y, e che inoltre x ¹ y. Per designare con un unico simbolo uno spazio ordinato, che è una "struttura" composta da due elementi, bisognerebbe utilizzare qualcosa del tipo X = (X,w ), ma per evitare spiacevoli appesantimenti si usa in genere indicarlo ancora, introducendo un "abuso di notazione", con la stessa lettera X che della struttura indica a rigore soltanto l'aspetto di puro insieme (X viene denominato il sostegno di (X,w )).

I due prototipi di spazio ordinato¹⁰, sono l'insieme dei numeri naturali N = { 1,2,3,...} e la retta ordinaria R¹¹, ed è questa la ragione di una terminologia "geometrica", in cui spesso e volentieri si sostituisce al termine "elementi" (di X) il termine "punti". Non si tratta però dei semplici "insiemi" in oggetto, in quanto essi si presentano indissolubilmente associati a un ordine, con una differenza alquanto istruttiva, a volerci speculare sopra (un'ulteriore diversità tra la concezione dello spazio e quella del tempo, vedi il par. 5 di "Zenone"). Mentre il primo insieme possiede una struttura d'ordine totale appunto "naturale", che tutti conoscono e utilizzano: 1 < 2 < 3 <..., il secondo ha due strutture d'ordine naturali, indistinguibili l'una dall'altra, e l'una opposta all'altra¹². Cioè, non esiste alcun ordine "naturale" in R, perché non ha senso chiedere quale, di due assegnati punti (posizioni) A e B, preceda l'altro: deve essere prima specificato un "verso di percorrenza" di R. Poiché si comprende sempre meglio quando è fornito, insieme a un esempio di ciò che viene affermato, anche un suo contro-esempio, osserviamo che un "ordinamento" naturale (ancora totale) esiste invece per i segmenti di R (vedi la nota 11 di "Zenone"): dati due di essi si può riconoscere se uno è minore o uguale dell'altro, oppure no. Siamo però di fronte a una relazione che viene chiamata precisamente di preordine, dal momento che non soddisfa una condizione ritenuta al contrario essenziale per l'ordine strettamente inteso, ossia l'anti-simmetria (cfr. la nota 9): x £ y insieme a y £ x non implica attualmente x = y, due segmenti possono essere "uguali" ma non "identici". [L'anti-simmetria non si verifica per relazioni di uso comune quali "y è preferibile a x", senza escludere però che le due alternative siano da ultimo "indifferenti", "equivalenti" - sulla "relazione d'equivalenza" associata a un preordine cfr. "dispense", (III.62).]

Anche se è comune riferirsi ai due enti nominati come a semplici insiemi, essi saranno qui per noi degli spazi ordinati, sottintendendo nel primo caso l'ordine naturale, nel secondo caso di aver scelto uno dei due ordini naturali. La situazione si chiarisce viepiù, se si vuole essere assolutamente rigorosi, tenendo in mente il seguente diagramma.
 
 

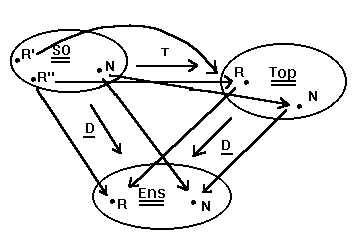
In esso sono rappresentati gli "oggetti" delle categorie di nostro precipuo interesse. Una è appunto la categoria degli spazi ordinati, , e le altre due sono quella degli insiemi, , e degli spazi topologici¹³, . Nella figura sono altresì illustrate le "relazioni" naturali tra dette categorie. Sia  che  stanno "sopra" , nel senso che ad ogni spazio ordinato, o ad ogni spazio topologico, si può sempre associare il relativo sostegno (rammentiamo, l'insieme su cui le date strutture sono assegnate). Le corrispondenze in parola (il termine tecnico è funtori, una generalizzazione alla teoria delle categorie del concetto di funzione, o meglio di "omomorfismo"; per quanto riguarda alcune nozioni preliminari concernenti le nozioni fondamentali qui utilizzate, compresa un'esatta definizione generale di isomorfismo, si veda la parte II del capitolo I delle "dispense") vengono descritte dalle due "frecce" che sono state indicate con la lettera  (due sottolineature stanno a segnalare una categoria, una sola un funtore), in ossequio all'iniziale della parola "dimenticante": si tratta cioè di operazioni che semplicemente dimenticano la struttura dell'ente, per restituire la sua nuda natura insiemistica (l'identità dei suoi elementi). Il problema è che sopra ad N e ad R, intesi come insiemi "privi di struttura", esistono infinite strutture diverse, sia in  che in . Tra tutte queste, se ne individua una speciale in , quella che abbiamo definito naturale, e quindi abbiamo continuato a designare il relativo spazio ordinato con il simbolo N - ma attenzione, che si sta introducendo un "abuso di notazione", conseguente peraltro a un "abuso di linguaggio". Per contro, esistono due strutture (spazi ordinati) altrettanto speciali, o "canoniche", sopra R in , a cui abbiamo allora riservato i nomi R' e R''. Scegliere una delle due, ossia uno dei due ordinamenti naturali in R, si dice anche aver orientato la retta (i due ordini in parola sono infatti anche chiamati orientamenti, o versi, di R; in conformità, R' e R'' si dicono pure rette orientate)¹⁴. "Sopra" a N e ad R in  c'è invece un'unica struttura naturale, e la motivazione è presto chiarita mediante l'introduzione di un'ulteriore corrispondenza, che abbiamo contrassegnato con la lettera T, tra gli oggetti di  e quelli di  (T gode ovviamente della proprietà che, se si opera prima T da  a , e poi  da  a , si ottiene lo stesso risultato che facendo direttamente  da  a ). Stiamo qui discutendo l'importante concetto di topologia associata, sempre sul medesimo sostegno X, a un ordine w , [in simboli
t_w ; uno spazio topologico su un insieme X si indica con la coppia ordinata (X,t ), dove t è appunto la fissata topologia su X - chiaramente, qui t non ha nulla a che fare con il tempo, ma i simboli sono pochi e le esigenze molte]. Si comincia con l'introdurre la semiretta di origine un dato elemento a dello spazio ordinato (X,w ), una nozione che comprende in realtà diversi casi:

- semiretta superiore chiusa, simbolo [a,+¥ ), totalità degli elementi x ³ a;
- semiretta superiore aperta, simbolo (a,+¥ ), totalità degli elementi x > a;
- semiretta inferiore chiusa, simbolo (-¥ ,a], totalità degli elementi x £ a;
- semiretta inferiore aperta, simbolo (-¥ ,a), totalità degli elementi x < a.

Corrispondentemente, se a £ b sono due qualsiasi elementi di X, non necessariamente distinti, si parla degli intervalli chiusi, aperti, semi-chiusi o semi-aperti, a destra o a sinistra, di estremi a e b: [a,b], (a,b), [a,b), (a,b], ove [a,b] = [a,+¥ )Ç (-¥ ,b] = { x Î X tali che a £ x £ b} , etc., con si spera ovvio significato dei simboli. [In "Zenone" abbiamo chiamato segmenti gli intervalli propri, cioè tali che a ¹ b, e chiusi, sicché il vuoto o un singleton (un insieme con un solo elemento), gli unici due casi in cui un ordine coincide con il suo opposto, non contengono segmenti. Un intervallo spaziale improprio, del resto, non solo non permette di ricostruire l'ordine della retta alla quale appartiene (ciò che è al contrario possibile per un intervallo proprio una volta che si sia assegnato un ordine ai suoi vertici), ma neppure la "direzione" di essa: per un fissato punto del piano, ad esempio, passano infinite rette. Per quanto riguarda invece i segmenti temporali, si può notare che uno di questi, oltre che chiuso per definizione, è anche aperto. L'intervallo chiuso [a,b] individuato da due istanti a, b (non necessariamente distinti) e l'intervallo aperto avente per vertici l'istante precedente di a e il successivo di b coincidono: [a,b] = (a-1,b+1), con simbolismo auto-esplicativo.] Nella nomenclatura sono già presenti alcuni attributi di natura topologica, quali "chiuso" e "aperto", e infatti si comincia a definire la topologia t_w asserendo che essa deve contenere almeno tutte le semirette aperte di X, sia superiori che inferiori. Dovrà poi contenere tutte le intersezioni finite di siffatte semirette, e quindi tutte le unioni (finite o infinite) delle intersezioni così ottenute. Alla fine di tali operazioni si perviene a una famiglia di insiemi (in termini tecnici, t_w si chiama la topologia generata dalla sottobase costituita da tutte le semirette aperte di X), gli aperti di X, che soddisfano gli assiomi previsti per la topologia (naturalmente, gli intervalli aperti risultano effettivamente aperti in questo senso, in quanto intersezione di due semirette aperte). Ecco la topologia t w di cui eravamo alla ricerca¹⁵, ossia: T((X,w )) = (X,t_w). L'effetto che più ci interessa della costruzione è che a uno spazio ordinato si possono sempre associare aggettivi specificativi tipici della topologia, per esempio avranno senso univoco espressioni del tipo lo spazio ordinato è connesso, o compatto, etc., per chi ne conosce il significato.

Nota*. E qui è doverosa un'importante osservazione. Prima di tutto, che abbiamo utilizzato il linguaggio delle categorie perché lo riteniamo il più adatto a illustrare con esattezza diversi fenomeni matematici, anche se non possiamo nemmeno accennare come conviene al fatto che nel concetto di categoria sono compresi tanto gli "oggetti" di essa quanto i relativi "morfismi", ossia le corrispondenze "ammesse" tra gli oggetti (qualche informazione la si può reperire nel cap. IV delle "dispense"). Affermare che una certa corrispondenza tra due categorie è un funtore (quindi qualcosa di più generale che le "semplici" corrispondenze tra oggetti, i.e. funzioni, o morfismi, denominazione appunto specificamente categoriale), significa che essa coinvolge non solo gli oggetti delle categorie, ma pure i relativi morfismi, in maniera "coerente". Bene, mentre i  sono veramente dei funtori nell'accennato preciso senso del termine (cioè, si può descriverne sia l'aspetto "oggettuale", sia quello "funzionale"), T decisamente non è un funtore (o, meglio, non può "diventarlo"), vale a dire, la corrispondenza tra  e  riguarda solamente gli oggetti, e non i morfismi. Se si vuol entrare nei dettagli, un morfismo d'ordine in  non è necessariamente un morfismo in , i.e. non è un'applicazione continua: basti pensare al caso dello spazio ordinato in modo naturale costituito dai numeri razionali { 0 < ... < 1/8 < 1/4 < 1/2 < 1} , e alla corrispondenza da tale spazio X a R che manda tutti gli elementi in 1, eccetto 0, che viene mandato in 0, è chiaro che si tratta di un morfismo d'ordine, ma discontinuo. Gli isomorfismi d'ordine (le corrispondenze biunivoche che conservano l'ordine, ovvero mandano una coppia di elementi del dominio uno minore dell'altro in una coppia di elementi del codominio che sono ancora nella medesima relazione d'ordine, e viceversa) sono in effetti bicontinui (in un'unica parola, omeomorfismi, cioè corrispondenze biunivoche che conservano la topologia, nel senso che insiemi aperti vanno in insiemi aperti, e viceversa), ma la circostanza illustrata complica in ogni caso la situazione. Ad esempio, può accadere che un sottospazio ordinato Y di uno spazio ordinato (X,w ) (semplicemente un sottoinsieme Y di X, con l'ordine indotto dall'ambiente) abbia una topologia d'ordine associata che non coincide con la topologia indotta su Y dalla topologia t_w di X (la topologia d'ordine appare "meno fine" dell'altra), un fenomeno in cui ci imbatteremo ancora nel par. 7. Insomma, un non perfetto collegamento tra ordine e topologia, che forse è all'origine dei problemi che incontreremo nel confrontare le nostre definizioni relative al discreto e al continuo nella categoria dell'ordine, con gli "analoghi" (e maggiormente "di moda") concetti topologici.

Dato quindi uno spazio ordinato, possiamo associare ad esso uno spazio topologico sul medesimo sostegno. Viceversa, fissato uno spazio topologico, non è detto che la sua topologia sia definibile mediante l'introduzione di un ordine sul sostegno¹⁶. In ogni caso, pur ammesso che un tale ordine esista, esso non è in generale unico. A parte l'ovvio caso dell'ordine opposto, che dà sempre la stessa topologia, un esempio è già fornito dall'insieme dei numeri interi relativi Z = { 0,± 1,± 2,...} (dall'iniziale del tedesco Zahlen) con la banale topologia t che dichiara tutti i sottoinsiemi di Z aperti (una topologia che si può definire su un qualsiasi insieme sostegno X, e si dice discreta, un termine le cui connessioni con il "discreto" oggetto delle attuali indagini verranno studiate nel par. 3). t è sicuramente una topologia d'ordine su Z, e almeno due ordinamenti non isomorfi la inducono. Uno è: ...-2 < -1 < 0 < 1 < 2 <... (assieme ovviamente all'opposto), un altro: 0 < 1 < - 1 < 2 < -2 <... (il primo, pur essendo quello "canonico", non è un buon ordinamento, il secondo invece sì - cfr. la nota 8).

Nota*. Una conseguenza è che, se (X,w ) e (X',w') sono due spazi ordinati, e f : X ® X' una corrispondenza biunivoca bicontinua tra i due spazi topologici associati (X,t_w) e (X',t_w'), f non è necessariamente un isomorfismo d'ordine. Per esempio, se le topologie in questione sono discrete - vedi il prossimo paragrafo - gli omeomorfismi tra (X,t_w) e (X',t_w') sono semplicemente tutte le corrispondenze biunivoche tra X e X', mentre quelle che mantengono l'ordine sarebbero ovviamente assai meno. Si tratta di un ulteriore segno dei "difficili" rapporti tra teoria dell'ordine e topologia, con cui dovremo fare spesso i conti.

Tornando alle nostre questioni specifiche, R' e R'' non sono coincidenti, ma sono evidentemente isomorfe (in ; una simmetria rispetto a un punto costituisce manifestamente un isomorfismo), il che autorizza in qualche modo a continuare a usare un unico simbolo R, e a parlare della (si noti la presenza dell'articolo determinativo) retta ordinaria ordinata, in realtà una delle due rette orientate R' o R'' associate alla retta ordinaria. Inoltre, poiché un ordine o l'ordine opposto individuano la medesima struttura topologica, esiste invece un'unica retta ordinaria topologica, alla quale assegniamo quindi sempre lo stesso simbolo R (si parla, corrispondentemente, della topologia ordinaria, o naturale, sulla retta ordinaria, una topologia che è allora una "topologia d'ordine"; mentre, come abbiamo visto nella nota 16, la topologia naturale del piano ordinario P non è una topologia d'ordine). Lo stesso, a fortiori, per N: esiste un unico spazio topologico associabile a tale simbolo, ed è palese che la topologia d'ordine di N è quella che abbiamo detto discreta: tutti i sottoinsiemi di N infatti risultano aperti (e anche chiusi, i due termini non sono mutuamente escludentisi), dal momento ogni singleton di N è aperto.

3. Il discreto

Cominciamo finalmente a precisare cosa debba intendersi per discreto, che è il caso più facile. Uno spazio ordinato (X,w ) è discreto se soddisfa la proprietà:

(D) Per ogni x, y Î X, con x < y, esistono soltanto un numero finito di elementi z Î X tali che x < z < y (eventualmente nessuno, e allora si dice che y "copre" x).

E' chiaro che lo stesso N, tutti i suoi segmenti iniziali s _n = { 1,2,...,n} , più in generale ogni sottoinsieme di N con la struttura d'ordine indotta da quella naturale, sono spazi ordinati discreti - isomorfi a N, qualora siano infiniti, o a uno, e uno soltanto, dei detti segmenti iniziali s _n, se sono finiti (il sottoinsieme vuoto è un caso a parte, per cui si deve introdurre il valore n = 0, ma ricordiamo che 0 non è per noi un "numero naturale"). Non soddisfa invece la condizione (D) per esempio la struttura di buon ordinamento, sempre sull'insieme dei numeri naturali: 1 < 3 < 5 <...< 2 < 4 < 6 <... , cioè prima si mettono tutti i numeri dispari, e poi tutti i numeri pari. E' chiaro che tra 2 e 5, tanto per nominare una coppia "irregolare" dal punto di vista della (D), esistono infiniti elementi di N.

La determinazione di tutti gli insiemi discreti scaturisce dal:

I Teorema di classificazione. Ogni spazio discreto (X,w ) appartiene a una, e una soltanto, delle seguenti "famiglie":
(i) X è finito, ammette minimo e massimo (se non è vuoto), (X,w ) è isomorfo a un segmento iniziale s _n di N, con l'ordinamento indotto da quello naturale (eventualmente anche n = 0, se si vuole contemplare il caso dell'insieme vuoto);
(ii) X è infinito, ammette minimo ma non massimo, (X,w ) è isomorfo a N;
(iii) X è infinito, ammette massimo ma non minimo, (X,w ) è anti-isomorfo a N, ovvero è isomorfo allo spazio ordinato opposto di N, vale a dire anche, è isomorfo a -N, l'insieme dei numeri interi negativi, con l'ordinamento ancora "naturale": ...< -3 < -2 < -1;
(iv) X è infinito, non ammette né minimo né massimo, (X,w ) è isomorfo a Z, l'insieme dei numeri interi relativi, con la struttura d'ordine naturale: ...< -3 < -2 < -1 < 0 < 1 < 2 < 3... .

(Allo stesso modo che per (i), neppure a (iv) si accompagna un analogo "duale", relativo alla presenza di un anti-isomorfismo, che associa invece (ii) e (iii). E' chiara la motivazione di tale assenza nel caso finito, mentre nell'altro la ragione è da individuarsi nel fatto che i due spazi ordinati (Z,£ ) e (Z,£ ^op) sono isomorfi, tramite la corrispondenza insiemistica x ® -x. Ciò non si verifica per gli spazi (N,£ ) e (N,£ ^op), che non sono isomorfi (il primo è un insieme bene ordinato - vedi la nota 8 - il secondo no), d'onde la necessità di procedere come si è fatto.)

(Dal I teorema di classificazione si può ottenere un'informazione importante sul sostegno X di uno spazio discreto (X,w ): esso è in ogni caso finito o numerabile. Il primo attributo non abbisogna di spiegazioni, il secondo significa che X si può mettere in corrispondenza biunivoca con l'insieme dei numeri naturali N, ossia che tutti i suoi elementi possono venire numerati in una successione del tipo: primo, secondo, etc.. Si noti bene però che questa numerazione non ha a priori nulla a che fare con la relazione d'ordine w , per esempio, Z si può numerare ponendo: 0 = primo, 1 = secondo, -1 = terzo, 2 = quarto, -2 = quinto, etc., ma tale ordinamento è completamente diverso dall'ordinamento naturale di Z, che compare nella precedente (iv). Inoltre, si deduce che X è bene ordinato se e soltanto se appartiene a una delle prime due famiglie (i) e (ii). Infine, che uno spazio ordinato finito è sempre palesemente bene ordinato, discreto, e tanto isomorfo quanto anti-isomorfo a un spazio "canonico" s _n, con l'ordinamento naturale.)

Dim. Supponiamo dunque di avere uno spazio discreto (X,w ), d'ora in avanti semplicemente X, che non sia finito (nel qual caso l'asserto del teorema è banale), e fissiamone un elemento a. Consideriamo poi l'insieme Mg(a) dei maggioranti di a in senso stretto,
Mg(a) = { x Î X tali che x > a} , e l'insieme Mn(a) dei minoranti di a in senso stretto,
Mn(a) = { x Î X tali che x < a} . Se Mg(a) è vuoto, a è il massimo di X (ovvero, per ogni elemento x Î X risulta x £ a), e ogni elemento x₁ Î X, x₁ ¹ a, è certo minore di a, x₁ < a. In virtù dell'ipotesi ammessa (X discreto), tra x₁ e a c'è solo un numero finito di elementi, sicché, essendo X supposto anche infinito, esisterà certamente un elemento x₂ Î X tale che x₂ < x₁. Ma anche tra x₂ e x₁ c'è solo un numero finito di elementi, perciò possiamo senz'altro determinare una successione di elementi di X del tipo: ... < x₃ < x₂ < x₁ < a, e tra x₂ e a ci sarà almeno un elemento, tra x₃ e a ci saranno almeno due elementi, etc.. Assegnato adesso un qualsiasi elemento z Î X, riuscirà certamente z < a, e tra z e a ci sarà solo un numero finito di elementi, diciamolo k, così, andando a confrontare tra loro z e x_k+1, non potrà certamente essere z < x_k+1, e quindi dovrà risultare necessariamente z ³ x_k+1. Si comprende facilmente come in questo caso X risulti anti-isomorfo a N. L'elemento a corrisponde al numero 1; l'unico elemento x nell'intervallo (semiaperto superiormente) x₁ £ x < a che sia coperto da a (rammentiamo, tale cioè che tra x e a non vi siano altri elementi) corrisponde al numero 2; etc.. Ragionando in maniera analoga, se Mn(a) è vuoto, a risulta il minimo di X, e X è isomorfo a N. Se Mg(a) non è vuoto, due sono i casi: o Mg(a) è finito, X ammette massimo b ¹ a, e resta comunque anti-isomorfo a N, oppure Mg(a) è infinito, e X non ammette massimo. Questa alternativa si spezza in due sotto-alternative: o Mn(a) è finito, e allora X ammette minimo, e rimane isomorfo a N, oppure Mn(a) è infinito, X non ammette né minimo né massimo, ed è chiaramente isomorfo a Z. L'elemento a si può far corrispondere al numero 0; il primo elemento coperto da a "alla sinistra" di a al numero -1; il primo "alla destra" di a al numero 1; etc.¹⁷, q.e.d..

Come illustrato in "Zenone", a nostro parere la retta temporale viene "intuita" nella fattispecie di uno spazio discreto del tipo (iv), ma ogni famiglia elencata nel teorema di classificazione appare comunque collegata alla nozione comune di "tempo". Spazi discreti del tipo (ii) corrispondono alla descrizione del futuro, quelli del tipo (iii) invece del passato, mentre (iv) raffigurerebbe, ripetiamo, tutto il tempo, passato e futuro. Anche il caso (i) (prescindendo dall'insieme vuoto, che costituisce una struttura a sé, sempre un po' particolare - il non-tempo, o la non-vita) ammette un'interpretazione temporale, rappresentando gli istanti di una singola esistenza (limitata). Il singleton s ₁ potrebbe considerarsi un "modello" dell'istante presente, laddove s ₂ avrebbe la medesima funzione per il minimo segmento temporale (il "cronone", cfr. "Zenone", par. 9).

Quanto precede ci mette ormai in grado di paragonare la definizione proposta con altre. Abbiamo affermato che si può dire (e lo si fa) che uno spazio topologico (X,t ) è discreto se la topologia t è discreta, ma è ovvio che tale nozione ha poco a che fare con la nostra, e riveste quindi per noi scarso interesse, principalmente perché una topologia discreta la si può definire su qualsiasi insieme (una sola, palesemente, il che autorizza l'uso dell'articolo determinativo: la topologia discreta t su un dato insieme X), di qualsiasi "potenza". Perciò, e allo scopo di evitare fraintendimenti, preferiremo in ogni caso parlare di "topologia discreta", e non di "spazio topologico discreto". I due concetti di "discreto", in topologia e in teoria dell'ordine, sono bensì connessi, ma solo alla lontana. Si può dimostrare infatti che sussiste il seguente:

Teorema 1. Se t è la topologia discreta su un insieme X, essa è sempre indotta da un ordine.

Dim*. Naturalmente, la dimostrazione del teorema 1 è immediata se X è un insieme finito o numerabile. In tal caso ogni numerazione di X (eventualmente "parziale") fornisce un ordine (totale) della specie desiderata. In generale, e supposto senz'altro che X sia infinito, la dimostrazione consiste in una tipica applicazione del Lemma di Zorn [vedi l'appendice al cap. III delle "dispense", in particolare la dimostrazione del teorema (III.A.12)]. Si considera l'insieme I di tutte le coppie ordinate (Y,w ), dove Y è un sottoinsieme di X, e w una relazione d'ordine su Y che induce su Y la topologia discreta. I è certo non vuoto, perché tutti i sottoinsiemi finiti di X compaiono quali primi elementi in una di siffatte coppie ordinate, ed è possibile ordinarlo parzialmente ponendo (Y,w ) £ (Y',w ') se e soltanto se Y Í Y', e w è la restrizione di w ' a Y. E' chiaro che I diventa così quello che si dice un insieme parzialmente ordinato induttivo, che ammette allora certamente elementi massimali. Sia (Y°,w °) uno di questi, il nostro scopo è dimostrare che Y° coincide con X. Bene, se fosse Y° Ì X, detto x un elemento di X non appartenente a Y°, potremmo prendere in esame l'insieme Y^# = Y°È { x} , e su di esso introdurre un ordine (totale) w ^# che induca su Y^# la topologia discreta, contraddicendo così l'ipotesi di massimalità di (Y°,w °). Per la definizione di w ^# si deve notare che, nelle attuali ipotesi, ogni elemento y di Y° diverso dagli eventuali minimo e massimo gode della proprietà che esistono due elementi a, b Î Y° tali che a < y < b (nella relazione d'ordine
w°), e che non esistono altri elementi di Y° né tra a e y, né tra y e b [il singleton { y} deve infatti risultare un aperto di Y°, e quindi risultare intersezione di due semirette aperte di Y°, appunto due insiemi del tipo (-¥ ,b) e (a,+¥ )]. Basta aggiungere x a Y° nel seguente modo: a < y < x < b, e il gioco è fatto.

Nota*. Un'altra dimostrazione, forse più semplice, si poggia sul lemma: se (X,w ) è un qualsiasi spazio ordinato, la topologia associata all'ordinamento lessicografico nel prodotto cartesiano X´ Z è discreta [ogni elemento (x,n) Î X´ Z risulta infatti l'unico elemento nell'intervallo aperto di estremi (x,n-1) e (x,n+1)]. Per provare il teorema 1, basta osservare che, se X è un insieme infinito, esso ammette sicuramente degli ordinamenti (totali), in forza per esempio dell'assioma del buon ordinamento [cfr. l'enunciato (III.A.6), nella citata appendice al cap. III delle "dispense"], e che X e X´ Z sono comunque equipotenti [cfr. il teorema (V.38) nel cap. V delle "dispense"].

Si può provare inoltre, e assai più facilmente, che:

Teorema 2. La topologia d'ordine associata a uno spazio ordinato discreto (X,w ) è la topologia discreta.

Però non è vero che, viceversa, uno spazio ordinato (X,w ) tale che la topologia indotta sul suo sostegno sia discreta, è necessariamente uno spazio ordinato discreto. Per avere un esempio di quest'asserzione, che ci offre l'occasione di familiarizzare un po' con la nozione di topologia associata a un ordine, si prendano due punti A e B sulla retta ordinaria orientata R (supponiamo A < B), e si dica M il loro punto medio. Consideriamo poi il punto medio tra A e M, indichiamolo con il simbolo S₁ (S sta per l'iniziale di "sinistra", sinistra di M), e il punto medio D₁ tra M e B. Ripetiamo la costruzione introducendo S₂, il punto medio tra S₁ e M, e D₂, il punto medio tra M e D₁, sicché, iterando il procedimento all'infinito, otteniamo due successioni di punti (distinti) A < S₁ < S₂ < ... < M < ... < D₂ < D₁ < B. Il sottoinsieme X di R costituito da tutti questi punti, eccettuato il punto M, costituisce uno spazio ordinato la cui topologia è certamente discreta, ma non è uno spazio ordinato discreto (tra ogni punto del tipo S e ogni punto del tipo D ci sono infiniti elementi). [Ogni punto C Î X diverso da A e B è un aperto - si dice così, senza stare a distinguere in maniera pedante tra C e { C} - in quanto l'insieme { C} risulta intersezione di due semirette aperte, per esempio
{ S_3} = (-¥ ,S₄)Ç (S₂,+¥ ), mentre { R_3} = (-¥ ,R₂)Ç (R₄,+¥ ). Gli insiemi { A} e { B} sono invece proprio semirette aperte essi stessi, { A} = (-¥ ,S₁), { B} = (R₁,+¥ ).]

(Comprenderemo nel seguito che, anche se uno spazio ordinato (X,w ) tale che la topologia associata sia discreta non è necessariamente uno spazio ordinato discreto, esso non può essere comunque un continuo, neppure di I specie.)

(L'esempio analizzato dopo il teorema 2 appare quindi un altro caso di ordinamenti diversi, né opposti né isomorfi, che inducono la medesima topologia - vedi la fine del par. 2.)

Quanto precede chiarisce abbastanza le connessioni tra la teoria del discreto nella categoria dell'ordine e la teoria del discreto nella categoria degli spazi topologici, così come essa viene comunemente trattata. Passando dalla corrispondenza T al funtore  (da  ad ), quando, volendo, sarà sensato asserire che un insieme X è discreto? La risposta che ci si deve attendere da un matematico "medio" di oggi è: quando X è finito o numerabile. Nel nostro quadro concettuale, abbiamo invece di fronte due precise alternative: possiamo definire X discreto quando esiste uno spazio ordinato "al di sopra" di X che sia discreto, oppure quando tutti gli spazi ordinati sopra X siano discreti. Nel primo caso, X è necessariamente finito o numerabile, il che fa ricadere nella definizione comune. Nel secondo caso, X deve essere necessariamente un insieme finito. Dovendo scegliere, osserviamo che chiamare un semplice insieme numerabile "discreto", in virtù della circostanza che esistono ordini discreti su di lui, sembra poco significativo, dal momento che su un insieme numerabile esistono anche, come presto vedremo, degli ordini che non solo sono "non discreti", ma sono addirittura "ovunque non discreti", in un senso che preciseremo, e che considereremo uno degli aspetti fondamentali del "continuo". Insomma, per gli stessi motivi, un insieme infinito numerabile dovrebbe essere detto sia "discreto", sia "continuo", il che non è certo opportuno¹⁸.

Sottolineiamo piuttosto che, in forza del teorema 1, la questione in discorso si chiarisce se si aggiunge alla nuda struttura d'insieme quella di spazio topologico, anzi di spazio topologico con la topologia discreta, il che consente di discutere l'interessante quesito rivoltoci da un collega mentre stavamo redigendo il presente articolo: <<Ma le stelle del cielo sono un discreto?>>. Una prima risposta, da un punto di vista strettamente letterale, è naturalmente la seguente. Poiché l'espressione "le stelle del cielo" si riferisce a un insieme (finito o infinito che esso sia, non lo sappiamo, né mai, nella veste di esseri umani, lo potremo sapere - si tratta di una delle antinomie kantiane, di cui alla nota 7 di "Zenone"), e non a uno spazio ordinato, non sarà lecito asserire che esse costituiscono un discreto, che è attributo esclusivo del secondo tipo di enti. Volendo interpretare invece la domanda in un senso meno restrittivo, ecco che possiamo effettuare noi stessi delle precisazioni, che immaginiamo "sottintese". Riconosciamo allora il fatto indubitabile che, quando introduce il concetto di "insieme delle stelle del cielo", l'intelletto umano fa ricorso a un modo di dire per indicare un insieme che viene concepito quale un sottoinsieme X di punti dello spazio ordinario S (prescinde cioè dalla reale natura delle stelle, limitandosi al "punto" che a una di esse corrisponde nell'immagine mentale del cielo stellato). Così, l'insieme X non è in verità pensato nella veste di un semplice insieme privo di struttura, come poteva apparire su due piedi, bensì nella veste di sottospazio topologico di S, ivi considerata la "topologia naturale" (allo stesso modo di R, S ha un'unica sua propria topologia, anche se non è indotta da un ordine, vedi la nota 16). Orbene, la percezione diretta dell'insieme delle stelle (e la nostra attuale concezione teorica di questi particolari oggetti materiali) è siffatta da doversi ammettere che in quanto spazio topologico X ha la topologia discreta. Ovvero, la circostanza saliente dal punto di vista fenomenologico è che X si presenta a noi nella forma di un insieme di punti isolati (per ciascuno di essi, chiamiamolo x, esiste un intorno di x che contiene solo x, ma nessun altro elemento di X; ritorneremo sulla nozione nel prossimo paragrafo). Ciò premesso, è facile dimostrare¹⁹ che l'insieme in discorso è di conseguenza o finito, o infinito, ma nella seconda alternativa è al più numerabile. In entrambi i casi vale il teorema 1 (nella sua versione più immediata), ed esiste un ordine lineare su X tale che la topologia naturale di X (quella indotta cioè dalla topologia naturale dello spazio ambiente S) coincida proprio con la topologia d'ordine associata. Vale a dire, l'insieme delle stelle può sensatamente ritenersi discreto, una volta che si siano fatte però tutte le precedenti precisazioni.

4. Il continuo di I specie

Risolta abbastanza facilmente la questione del discreto, veniamo a quella più difficile del continuo. Cominciamo con il rilevare che uno spazio ordinato sarà non discreto semplicemente quando non sarà soddisfatta la condizione (C), ovvero se almeno per una coppia di suoi elementi x < y esistono infiniti elementi tra x e y. Orbene, assumeremo il verificarsi di tale circostanza per ogni coppia di elementi x, y di X come una prima e decisiva caratteristica di un insieme continuo. Precisamente, diremo che uno spazio ordinato (X,w ), è un continuo di I specie se esso contiene almeno due elementi (condizione introdotta al fine di evitare casi banali, di dover riconoscere cioè continuo il vuoto o un singleton) e risulta ovunque non discreto, ossia se per l'ordine w vige la seguente proprietà:

(C1) Per ogni x, y Î X, con x < y, esiste almeno un elemento z Î X tale che x < z < y.

[La lettera C sta chiaramente per l'iniziale di continuo, mentre il numero 1 sta ad avvertire che seguiranno altre simili condizioni di "continuità", (C2), etc.. In J.G. Rosenstein, loc. cit. nella nota 5, la condizione (C1) appare alla p. 25, e viene chiamata una condizione di "densità".]

In conseguenza di (C1), un continuo di I specie è costituito da un numero infinito di elementi (tra due dati elementi x e y, supposti esistenti, deve esistere un terzo elemento z, quindi un quarto tra x e z, e così via, appunto "all'infinito"), il che ci porterà a dover prendere in considerazione la teoria cantoriana degli insiemi infiniti. Nulla di complicato, ma solo una doverosa, e almeno per certi versi semplice, analisi degli insiemi infiniti: semmai è da sorprendersi come un simile studio sia arrivato in ritardo, e ciò la dice lunga su quanto i problemi fondazionali siano stati oggetto di scarsa attenzione da parte dei matematici per secoli ("prima", perché erano pochi, "dopo", e intendiamo l'era "moderna", perché occupati soprattutto nelle "applicazioni" - vedi pure la prima nota del par. 2 di "Zenone").

Come dicevamo, se uno spazio ordinato non è discreto (e quindi il suo sostegno è certamente infinito), esso non è automaticamente ovunque non discreto, anche se si tratta di un sostegno semplicemente numerabile. Si pensi al già discusso ordinamento 1 < 3 < 5 <...< 2 < 4 < 6: tra 5 e 2 ci sono infiniti elementi, ma non tra 2 e 6, o tra 5 e 77. Pure l'unione X di due segmenti  e  disgiunti della retta ordinaria (vedi la seguente figura), scelto in essa uno dei due ordinamenti naturali (in cui supponiamo per esempio A < B < C < D), è uno spazio ordinato non discreto, che però non è un continuo di I specie: tra B e C non ci sono elementi di X.
 
 

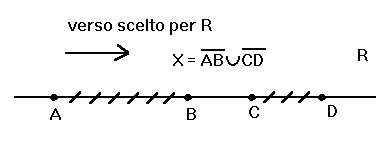
(X è un tipico esempio di spazio, ordinato o topologico, sconnesso, vedi il par. 7. Con riferimento alla nota di cui al par. 2, si osservi che in questo caso c'è coincidenza in X tra topologia dell'ordine e topologia indotta dall'ambiente.)

Ovviamente, l'archetipo della nozione è costituito dalla retta ordinaria, nella quale si fissi uno dei due ordinamenti naturali: tra due punti si è costretti a riconoscerne infiniti, se si ammette per esempio il postulato dell'esistenza del punto medio:

(M) Per ogni coppia di punti A, B Î R, con A ¹ B, esiste un (unico) punto medio M tale che i due segmenti  e  sono "uguali" (ribadiamo, non "identici", bensì uguali nel senso che ciascuno dei due è minore o uguale dell'altro nella fondamentale struttura di preordine cui si accennava nel par. 2).

Nota. Ribadiamo (vedi ciò che si dice sull'adaequatio nel par. 7 di "Zenone"), che i "postulati" - o gli "assiomi", modernamente si tende a non distinguere tra i due termini, o non si riesce a farlo! - sono semplicemente, almeno in un primo momento, asserti "elementari" relativi al modo con cui si concepisce un ente "noto" del pensiero. Quanti punti ci sono sulla retta dipende quindi da quanti noi siamo in grado, o "costretti", a percepirne, spesso non subito, ma in seguito a ragionamento.

Anche se oggi è invalso l'uso di considerare "continuo" solo il continuo che chiameremo di III specie (la retta ordinaria risulterà invero un siffatto continuo), ci sembra che l'illustrazione più adeguata del termine si ottenga mediante la proprietà (C1). La definizione corrisponde a quella proposta da Aristotele (con l'avvertenza però di distinguere opportunamente tra segmenti, cui è applicabile l'infinita suddivisibilità, e punti; cfr. la nota 11 di "Zenone"), secondo il quale è continuo <<ciò che è divisibile in parti sempre divisibili>> (Fisica, VI, 2). Essa spiega perfettamente la contrapposizione descritta in "Zenone" tra l'ordinaria percezione dello spazio e l'analoga percezione del tempo: in uno spazio ordinato discreto si può sempre parlare di elemento successivo a uno dato (quando l'insieme sostegno dello spazio ordinato sia costituito da almeno due elementi, e si tralasci l'eventuale massimo dello spazio ordinato), mentre ciò nel continuo non è assolutamente fattibile.

Nota. Chiariamo bene che ciò non significa che l'operazione di "successivo" possa effettuarsi esclusivamente in spazi ordinati discreti, infatti essa è lecita per esempio in ogni spazio bene ordinato (che in generale non sarà discreto). Si possono trovare anzi spazi ordinati non discreti nei quali non solo ogni elemento ha un successivo, ma anche ogni elemento ha un precedente, come accade nel caso discreto dei numeri interi relativi Z (con l'ordinamento naturale). Basta pensare al seguente nuovo ordinamento su Z: -3 < -1 < 1 < 3 < ... < -4 < -2 < 0 < 2 < 4 (allo stesso modo dell'altro, non è un "buon" ordinamento). In un ibo (usiamo la sigla introdotta nella nota 8) non vuoto (X,w ) si potrebbe chiedere al massimo che ogni elemento distinto dal primo abbia un precedente, ma tale condizione implicherebbe che (X,w ) è addirittura uno spazio discreto, isomorfo a N. Stiamo qui "giocherellando" in sostanza con la descrizione che dell'aritmetica viene fornita dai famosi cosiddetti assiomi di Peano: 0 è un numero (noi preferiamo decisamente 1); il successivo di un numero è un numero; 0 non è il successivo di alcun numero (0 non ha precedente); se due numeri x e y hanno lo stesso successivo allora x = y; vale il principio di induzione completa. [O induzione finita, per distinguere da un analogo principio di induzione transfinita che sussiste per ogni ibo (X,w ): banalmente, se Y è un sottospazio di X, che contiene il primo elemento x₁ di X, e l'elemento x tutte le volte che contiene la sequenza iniziale [x₁,x), allora Y = X (si noti però che negli assiomi di Peano non si fa riferimento a priori ad alcuna struttura di buon ordinamento). Per il principio di induzione completa vedi (II.12) nel II capitolo delle "dispense".]

Dal punto di vista topologico, un continuo di I specie viene comunemente collegato alla nozione di densità topologica, una nozione che si rifà all'importante concetto di punto di accumulazione: un continuo di I specie risulterà sempre denso in sé. Spieghiamo. Dato uno spazio topologico (X,t ), e un qualsiasi sottoinsieme X' Í X, notiamo prima di tutto che X' è univocamente il sostegno di uno spazio topologico (X',t '), e che perciò si parla anche di sottospazio topologico di (X,t ). Si introduce in X' la topologia costituita da tutte le intersezioni degli aperti di t con X'. Ciò premesso, si dice che un punto x Î X è un punto di accumulazione per X' se ogni intorno di x contiene punti di X' distinti da x, condizione che ha efficacia naturalmente quando x stesso è in X'. In questo caso, se x non è un punto di accumulazione per X', ovvero se esiste un intorno di x che contiene solo x tra gli elementi di X', allora x si chiama un punto isolato di X' (un punto isolato è tale che il singleton { x} è un aperto in X'; le finalità dell'intera nomenclatura sono piuttosto evidenti). L'insieme dei punti di accumulazione in X di un suo sottoinsieme X' viene definito il derivato di X', in simboli D(X'). X' sarà costituito da tutti punti isolati, come l'insieme delle stelle del cielo di cui al paragrafo precedente, se e soltanto se X'Ç D(X') = Æ . [Osserviamo che, se D(X') = Æ , allora certamente i punti di X' sono tutti isolati, ma che può essere X'Ç D(X') = Æ anche qualora D(X') ¹ Æ . Si pensi all'insieme X' dei numeri 1, 1/2, 1/3, etc. in R: 0 è un punto di accumulazione di X' in R che non appartiene a X'.] X' si dice denso su un altro sottoinsieme non vuoto X'' qualora X'' Í D(X'), ossia quando tutti i punti di X'' sono punti di accumulazione per X'. X' si dice finalmente denso in sé se non è vuoto e se risulta X' Í D(X'), cioè se tutti i punti di X' sono punti di accumulazione per X' (in altri termini, quando X' non possiede punti isolati)²⁰. [L'esempio più comune è quello dell'"insieme" dei numeri razionali Q, che risulta denso sull'insieme di tutti i numeri reali R: R Í D(Q); anzi, poiché necessariamente D(Q) Í R, ecco che risulta R = D(Q). Dalla precedente relazione R Í D(Q) si deduce a fortiori Q Í D(Q), ovvero che Q è denso in sé, e lo stesso accade per R, R Í D(R).] E' chiaro che in un continuo di I specie, poiché tutti gli aperti che contengono un determinato punto x di X devono contenere infiniti punti di X, in particolare punti di X diversi da x stesso, ogni punto risulta un punto di accumulazione (in X non esistono punti isolati). Si tratta però di una condizione di continuità che è solo necessaria: infatti uno spazio ordinato può essere denso in sé, ma non è ancora necessariamente un continuo di I specie, come mostra palesemente l'esempio dello spazio X di cui alla figura precedente [la "densità topologica" non coincide con la "densità ordinale"; vedi quanto si diceva in sede di commento alla (C1), citando il libro di J.G. Rosenstein]. Nelle seguenti parole di Bolzano, interessanti per le anticipazioni "topologiche" in esse contenute, tale distinzione non sembra essere colta: <<siamo costretti a dichiarare di essere in presenza di un continuo quando, e solo quando, si abbia un aggregato di entità semplici (istanti, o punti spaziali, o anche sostanze), disposte in modo che ogni singolo elemento dell'aggregato abbia, ad ogni distanza da se stesso arbitrariamente piccola, almeno un altro elemento dell'aggregato>> (loc. cit. nella nota 17 di "Zenone", p. 70).

Approfondiamo l'analisi del continuo di I specie tornando al caso della retta ordinaria R, orientandola nella successiva figura sempre da sinistra a destra, come prima. Fissati due punti A e B di R, con A che precede B, possiamo "traslare" il segmento  tante volte alla destra di B, in modo da ottenere la successione B, B', B'', ... , e lo stesso alla sinistra di A, fino ad ottenere la successione -B, -B', -B'', ... con ovvio significato dei simboli.
 
 

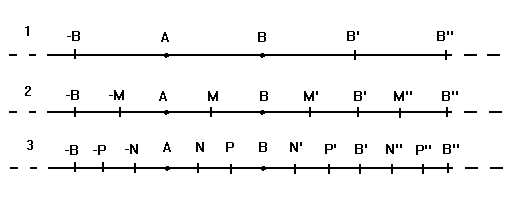
A partire da A e B, abbiamo così introdotto un primo sottospazio ordinato di R, che indicheremo con il simbolo D (A,B) (è chiaro che D (A,B) = D (B,B') = D (-B,A) etc.). In D (A,B) risulta manifestamente ...< -B' < -B < A < B < B' <... . Possiamo poi, ancora con riferimento alla figura, costruire l'insieme D ₂(A,B), il sottospazio ordinato di R costituito da tutti i punti di D (A,B), più tutti i punti medi dei segmenti formati da punti consecutivi di D (A,B). Allo stesso modo, usando la tricotomia in luogo della dicotomia, possiamo parlare di D ₃(A,B), etc.. E' evidente che si tratta di tutti spazi ordinati discreti, tra loro isomorfi (isomorfi a Z, caso (iv) del I teorema di classificazione), per quanto la "distanza" tra due punti successivi della decomposizione venga ridotta²¹. In effetti, D ₂(A,B) = D (A,M), il che dimostra che si ha a che fare in sostanza con la medesima struttura. Possiamo però considerare gli insiemi:

W ₂(A,B) = D (A,B)È D ₂(A,B)È D ₄(A,B)È ...
W ₃(A,B) = D (A,B)È D ₃(A,B)È D ₉(A,B)È ..., etc.,

ottenuti a partire da un numero intero n maggiore di 1, n = 2, 3,... , e poi iterando il procedimento di decomposizione per successive potenze di n (2, 2², 2³, ... ; 3, 3², 3³,...), oppure anche l'insieme:

W (A,B) = W ₂(A,B)È W ₃(A,B)È W ₄(A,B)È ... = D (A,B)È D ₂(A,B)È D ₃(A,B)È ...

Sarà utile poi definire i seguenti spazi ordinati:

- (A,B)₂, il sottoinsieme di W ₂(A,B) costituito dai punti compresi tra A e B, estremi esclusi;
- [A,B)₂, il sottoinsieme di W ₂(A,B) costituito dai punti compresi tra A e B, A incluso e B escluso;
- (A,B]₂, il sottoinsieme di W ₂(A,B) costituito dai punti compresi tra A e B, A escluso e B incluso;
- [A,B]₂, il sottoinsieme di W ₂(A,B) costituito dai punti compresi tra A e B, estremi inclusi;

e se si vuole (A,B)₃, etc..

Nota (importante). Ogni spazio ordinato D (A,B) corrisponde a un'immersione della retta temporale T nella retta spaziale R, ovvero a un'immagine, una rappresentazione, di T dentro R. Ma mentre stiamo riconoscendo "inadeguata" una riduzione dello spazio al tempo (del continuo geometrico al discreto aritmetico), allo stesso modo sarebbe assurdo voler tentare una riduzione "inversa" del tempo allo spazio, sulla base di questo naturale e banale risultato!

Ecco che abbiamo finalmente una serie di spazi ordinati che non sono discreti, e anzi sono dei continui di I specie. Tali spazi (ciascuno dei quali non esaurisce tutti i punti di R²²) sono però numerabili, come dimostra il "I teorema di Cantor" (si veda la figura che ne sintetizza la semplice dimostrazione nel V capitolo delle "dispense"), e ciò implica l'esistenza di una forte connessione tra di loro, non solo nella veste di insiemi, ma appunto in quella di spazi ordinati. Per esempio, gli spazi W ₂(A,B), W ₃(A,B), ... W (A,B), (A,B)₂, etc., che sono privi di minimo e di massimo, risultano tra loro isomorfi. Ciò costituisce l'oggetto del seguente, per noi fondamentale (cfr. J.G. Rosenstein, loc. cit. nella nota 5, pp. 26-27):

II Teorema di classificazione. Un continuo di I specie numerabile è sempre isomorfo a uno, e uno soltanto, dei seguenti spazi:
(i) (A,B)₂ (caso in cui lo spazio non ha né minimo né massimo)
(ii) [A,B)₂ (caso in cui lo spazio ha minimo, ma non massimo)
(iii) (A,B]₂ (caso in cui lo spazio ha massimo, ma non minimo)
(iv) [A,B]₂ (caso in cui lo spazio ha sia minimo che massimo)

(Ovviamente i due casi (ii) e (iii) sono anti-isomorfi.)

Corollario. Due continui di I specie numerabili senza minimo e senza massimo sono sempre tra loro isomorfi.

Dim. Basterà naturalmente dimostrare che un dato spazio ordinato (X,w ) con sostegno X numerabile, privo di minimo e massimo, è isomorfo a (A,B)₂, gli altri tre casi riconducendosi agevolmente a questo. Si introduca all'uopo una numerazione x₁, x₂, x₃, ... di X (che non avrà nulla a che fare con l'ordine di X, vale a dire, non sarà vero in generale che x₁ < x₂ etc.), e si costruisca il desiderato isomorfismo f : (A,B)₂ ® X in modo progressivo. Si ponga cioè

f(1/2) = x₁,
f(1/4) = primo elemento di X (nella data numerazione) che sia alla sinistra di x₁
f(3/4) = primo elemento di X che sia alla destra di x₁
f(1/8) = primo elemento di X che sia alla sinistra di f(1/4)
f(3/8) = primo elemento di X che sia compreso (in senso stretto) tra f(1/4) e f(2/4) = f(1/2)
f(5/8) = primo elemento di X che sia compreso tra f(2/4) e f(3/4)
f(7/8) = primo elemento di X che sia alla destra di f(3/4)

etc.. (si noti che 2/4 = 1/2 era già compreso nel livello precedente al secondo, così come
2/8 = 1/4, 4/8 = 1/2, e 6/8 = 3/4 nei livelli precedenti al terzo, etc.).

Il punto chiave della dimostrazione consiste nel fatto che, se per esempio x₅ è il primo elemento di X alla sinistra di x₁, allora x₂, x₃, x₄ si trovano alla destra di x₁, sicché, in tale caso, f(3/4) = x₂, mentre x₃ risulterà necessariamente essere o f(5/8), o f(7/8), etc.. Insomma, tutti gli elementi di X vengono fuori prima o poi alla destra della precedente tabella, laddove tutti gli elementi di (A,B)₂ compaiono invece, "ordinatamente", alla sinistra, q.e.d..

Nota. L'isomorfismo costruito nella precedente dimostrazione è ben lungi dall'essere unico, o in qualche misura "canonico". Per ogni numerazione di X se ne determina uno, e poiché i primi k elementi della numerazione, per un qualsiasi numero naturale k, possono essere scelti in modo assolutamente arbitrario, ecco che valgono proposizioni del seguente tipo: "Due continui di I specie X e Y, numerabili, senza minimo e senza massimo, non solo sono sempre tra loro isomorfi, ma addirittura, comunque considerata una "catena" finita di punti di X (ovvero, un insieme finito di punti di X: x₁ < x₂ <...< x_k), e un'analoga catena finita di punti di Y, y₁ < y₂ <...< y_k, si può trovare un isomorfismo (d'ordine) tra X e Y soddisfacente alle condizioni f(x₁) = y₁, etc.". Detta non canonicità impedisce di trasferire da uno spazio ordinato a un altro, seppure essi siano isomorfi, caratteristiche addizionali che sono precipue per esempio della "natura" specifica degli elementi del primo, ma non del secondo. In un "generico" spazio continuo di I specie (X,w ), ammettiamo numerabile e senza minimo e massimo, non sarà possibile operare alcun "confronto naturale" tra segmenti (la struttura di preordine alla quale si accennava nel par. 2, nel caso di R, e dei suoi sottospazi ordinati), nonostante ciò si possa in (A,B)₂, e malgrado (X,w ) sia ad esso isomorfo (in ). Allo stesso modo, in (A,B)₂ non si potrà introdurre una somma ancora "naturale" tra classi di equivalenza di segmenti (e formulare l'assioma dell'archimedeicità, vedi nota 21), sebbene ciò sia lecito per i segmenti di W (A,B), che ad (A,B)₂ è isomorfo.

Nota*. Il II teorema di classificazione non è un caso particolare di un teorema più generale, vale a dire, non si può ripetere un'affermazione simile per continui di I specie che abbiano cardinalità (come abbiamo già avuto modo di informare, un sinonimo di "potenza") diversa dal numerabile (e quindi certamente superiore al numerabile, trattandosi comunque di insiemi infiniti). In parole più tecniche, lo scheletro della categoria  (pur limitandoci agli spazi ordinati senza minimo e senza massimo) è (assai) "più grande" dello scheletro della categoria  (i due scheletri coincidono soltanto per gli insiemi al più numerabili). Gli spazi Rⁿ, per ogni numero naturale n, con l'ordinamento lessicografico, costituiscono sicuramente dei continui di I specie (non numerabili), senza minimo e senza massimo, però essi sono non isomorfi per valori distinti della "dimensione" (si veda il paragrafo "Gruppi abeliani ordinati e gruppi archimedei", in http://www.dipmat.unipg.it/~bartocci/mat/cap10.doc).

In conclusione, abbiamo indagato un poco la nozione di spazio (spazio ordinato) continuo di I specie, scoprendo che il sostegno di una tale struttura è necessariamente infinito. Inoltre, che esiste "sostanzialmente" un solo tipo di siffatto spazio (a meno cioè di isomorfismi, e aggiungendo l'ipotesi che lo spazio sia privo di minimo e di massimo) nell'ambito del numerabile. Esistono però tanti altri spazi continui di I specie di potenza superiore al numerabile, una cui classificazione è impresa difficile.

5. Il continuo di II specie

Riprendiamo l'analisi dal fatto che può darsi un unico tipo di continuo (di I specie) numerabile senza minimo e senza massimo, e che diversi di questi spazi ordinati si possono pensare quali sottospazi della retta ordinaria orientata R. Ma R essa stessa, costituisce o no uno dei continui di I specie in parola, ossia, R si può cioè ritenere numerabile? Abbiamo già osservato che W (A,B) non può coincidere con l'intero R, come conseguenza delle riflessioni sulla "necessità" dell'irrazionale, ovvero, secondo il nostro punto di vista, sulle ineludibili caratteristiche della maniera di concepire lo "spazio" da parte dell'intelletto umano. Le relative dimostrazioni si poggiano usualmente su considerazioni geometriche in ambiente bidimensionale (diagonale di un quadrato, diagonali di un pentagono regolare, sezione aurea, etc.), o algebrico-aritmetiche (assurdità di un numero razionale, di un rapporto di numeri interi, il cui quadrato sia un numero primo), sicché tutti i numeri irrazionali "costruiti" sin dai primordi sono di una famiglia assai speciale, dei numeri algebrici. In breve, "radici" di equazioni algebriche (in una incognita) a coefficienti interi, per esempio radici (quadrate o d'ordine superiore) di qualche numero intero (positivo), radici di siffatte radici, loro "combinazioni", etc.. Per contro, si chiamano numeri trascendenti quei numeri (ancora espressione di misure di coppie di segmenti, numeri reali) che non sono algebrici, sull'eventuale "esistenza" dei quali non ci sembra che l'intuizione possa asserire qualcosa in modo "immediato". Però, anche se si aggiungessero all'insieme W (A,B) i punti P tali che il segmento AP abbia rispetto ad AB una misura algebrica, pur ottenendo un insieme assai "più grande" apparentemente di quello di prima, ecco non usciremmo comunque dall'ambito del numerabile, come non è troppo difficile dimostrare, sempre in virtù del I teorema di Cantor (i polinomi in una indeterminata a coefficienti interi e di grado 0 sono manifestamente un'infinità numerabile, così quelli di grado 1, di grado 2, etc., e perciò tutti; poi ciascun polinomio ha al più un numero finito di radici reali, insomma i numeri reali algebrici costituiscono un'infinità numerabile). La domanda d'apertura rimane così in piedi: R si può pensare numerabile? (anche se si avesse contezza di qualche numero reale trascendente, si potrebbero aggregare i punti che lo "rappresentano" all'insieme dianzi costruito, con la conseguenza di rimanere nell'ambito del numerabile).

A questo punto è interessante porsi il quesito: qual è l'aspettativa naturale di fronte all'interrogativo in oggetto? Dovrebbe essere forse quella di concepire i punti della retta come una totalità numerabile (esisterebbe cioè, fatte salve ulteriori considerazioni, un unico tipo di infinito), ma non è così, e siamo in grado di rendercene perfettamente conto, date solo le semplici verità fin qui raccolte. C'è infatti una proprietà che il "continuo" della retta soddisfa, a differenza di ogni continuo numerabile finora nominato (e che si possa mai nominare, poiché sono tutti "classificati" dal II fondamentale teorema precedente), ed essa è talmente "antica" che preferiamo ricorrere per illustrarla a semplici ragionamenti classici, senza scomodare i "mandarini" tedeschi dell'ultima parte del XIX secolo.

Digressione. Un esempio dell'applicazione del "postulato" del quale stiamo implicitamente parlando, ancorché si debba arrivare i tempi di Cantor e Dedekind per vederlo formulato e discusso con l'opportuna cura, è fornito dall'introduzione del celebre numero p , ovvero dall'esistenza stessa del concetto di lunghezza L di una circonferenza, che è collegato all'esistenza di un segmento rettificante la curva in oggetto, la cui misura rispetto a un segmento prescelto come unità di misura corrisponderà appunto alla lunghezza L. Nella seguente figura si vedono una circonferenza e un quadrato in essa iscritto, assieme a un quadrato circoscritto.
 
 

E' chiaro che, riportando i quattro segmenti , , ,  consecutivamente sulla retta R, diciamo a partire da un qualsiasi punto "origine" P, si ottiene un punto Q tale che il segmento  rappresenta il perimetro del quadrato. La misura di , rispetto a un'unità di misura fissata in modo arbitrario, è palesemente minore della lunghezza L, della cui definizione siamo in cerca. Se facciamo altrettanto con i quattro segmenti , , , , ricaviamo un segmento  la cui misura sarà invece maggiore di L. Se aumentiamo il numero dei lati del poligono regolare iscritto nella circonferenza, otteniamo un numero più grande di quello di prima, tuttora però minore di L. Analogamente, il poligono regolare circoscritto con il medesimo numero di lati avrà un perimetro minore del precedente, comunque ancora maggiore di L. Insomma, otteniamo tanti punti Q, e tanti punti Q', nessuno dei quali dà, come misura di  o , esattamente L (poiché la circonferenza non coinciderà mai con alcuno di questi poligoni, per quanto alto si possa prendere il numero dei lati). Malgrado ciò assumiamo, per intuizione diretta della natura dello spazio (della retta), che esiste un (unico) punto X tale che PX è maggiore di tutti i PQ, allo stesso modo che PX è minore di tutti i PQ', ovvero tale che la misura di PX sia proprio la ricercata L, senza alcuna "approssimazione"²³.

Per farla breve, il postulato a cui soddisfa la retta ordinaria (orientata) R, e che viene pertanto chiamato il postulato di continuità di R, è il seguente:

(C2) Dato un qualsiasi insieme non vuoto X di punti di R che sia superiormente limitato, tale cioè che esista un maggiorante M per tutti i punti di X (P < M, per ogni P Î X), esso ammette un estremo superiore E(X), ovvero un minimo maggiorante (un maggiorante che sia più piccolo di ciascuno dei maggioranti di X).

(Indicato, conformemente a quanto effettuato nel corso della dimostrazione del I Teorema di classificazione, l'insieme dei maggioranti di X con il simbolo Mg(X), nel caso precedente Mg(X) è supposto non vuoto in virtù dell'ipotesi di limitatezza. Si noti che E(X) appartiene certamente a Mg(X), ma non è detto che appartenga a X: potrebbe o non potrebbe essere un elemento di X. Nel caso della circonferenza, poiché nessun perimetro di un poligono regolare iscritto coincide con L, ecco che E(X) = L non appartiene all'insieme X di cui trattasi).

Naturalmente, il postulato (C2) potrebbe essere riformulato per gli insiemi inferiormente limitati, in relazione all'esistenza quindi di un estremo inferiore e(X) per ogni insieme X di punti di R che sia inferiormente limitato, oppure nella seguente forma "complessiva":

(C2') Dato un qualsiasi insieme non vuoto limitato X di punti di R (un insieme X che sia cioè tanto superiormente, quanto inferiormente limitato), esso ammette sia un estremo superiore E(X), sia un estremo inferiore e(X).

Si possono trovare numerose altre forme istruttive del postulato in oggetto (vedi http://www.dipmat.unipg.it/~bartocci/mat/continuit.doc), introducendo i concetti di "coppia di classi contigue", di "elemento di separazione", etc.. Personalmente troviamo assai significativa la:

(C2'') Quando si immagina un insieme non vuoto limitato X di punti di R, è impossibile non concepire simultaneamente il minimo segmento in cui esso è contenuto.

Ci preme osservare che tutti questi postulati equivalenti (C2) etc. possono proporsi per un qualsiasi spazio ordinato, e si comprenderà perché denomineremo continuo di II specie ogni spazio ordinato che sia un continuo di I specie e in più soddisfi (C2).

Nota. (C2) da solo, che si dice pure postulato di completezza (cfr. J.G. Rosenstein, loc. cit. nella nota 5, p. 33), può valere anche in spazi nei quali non è verificata (C1). Per esempio ogni spazio discreto è senz'altro "completo", allo stesso modo che è completa l'unione dei due segmenti disgiunti rappresentati nella prima figura del paragrafo precedente, che ancora non è un continuo di I specie.

Per come è stata costruita la definizione, perveniamo a una prima ovvia conclusione:

Teorema 3. La retta ordinaria orientata è un continuo di II specie.

Una seconda, meno immediata, ma sempre "semplice", al punto in cui siamo arrivati, è che:

Teorema 4. Un continuo di I specie numerabile non può mai essere un continuo di II specie.

Basta infatti tenere presente il II teorema di classificazione. Un continuo di I specie numerabile, specifichiamo senza minimo e senza massimo, è necessariamente isomorfo ad (A,B)₂, ed è chiaro che (A,B)₂ non soddisfa (C2). L'insieme di tutti i punti di (A,B)₂ che sono minori del punto P tale che è uguale a 3 volte il segmento , non ha estremo superiore in (A,B)₂ - si presti attenzione alla circostanza che l'insieme in parola non è inferiormente limitato in (A,B)₂, perché il punto A non è un punto di (A,B)₂.

Insomma, un continuo di I specie numerabile non è mai completo, e poiché invece un continuo di II specie completo lo è per definizione, ecco che dai teoremi 3 e 4 consegue il:

Teorema 5. La retta ordinaria orientata non è numerabile.

Nota. A proposito di quanto si riferiva poc'anzi sui numeri reali trascendenti, dal teorema 5 si è edotti della circostanza che di siffatti numeri esiste un insieme infinito addirittura non numerabile. Altrimenti, sarebbe pure tale l'unione dei numeri algebrici e dei numeri trascendenti, cioè la classe di tutti i numeri reali R, che per definizione è equipotente ad R, ed R numerabile non è. Corrispondenze biunivoche tra R e R - nessuna però canonica, i due enti in questione non sono "identificabili" - sono fornite dalle cosiddette "coordinatizzazioni" di R. E' istruttivo osservare che la differenza tra algebricità e trascendenza appare di tipo fondamentale, ma che di essa la geometria greca non riuscì a rendersi conto, probabilmente per mancanza di una precisa comprensione della piena struttura algebrica posseduta dalla totalità di questi numeri. [Un passo importante, se non decisivo, verso la consapevolezza in parola fu sicuramente l'introduzione della geometria analitica da parte di Cartesio (1637), che coniuga algebra e geometria, calcolo e retorica, in modo fecondo, senza distruggere la specificità né dell'una né dell'altra.] Si potrebbe ritenere insomma che le prime speculazioni geometriche riguardassero la retta spaziale (l'"infinito") solo numerabile, sebbene fosse conosciuta (mediante intuizione naturale e perenne del fenomeno), e utilizzata, una sua proprietà, appunto la (C2), che è incompatibile con la numerabilità.

Il teorema 5 è noto come una delle conseguenze più famose del "II teorema di Cantor"²⁴ (vedi ancora il citato V capitolo delle "dispense"): la retta ordinaria (l'insieme dei numeri reali) non è numerabile. Una conclusione che può essere raggiunta però, come abbiamo visto, anche attraverso considerazioni relative alla pura struttura d'ordine, ed evitando il "procedimento diagonale"²⁵. Certo, giocano un ruolo essenziale le proprietà geometriche accessorie di uno spazio ordinato quale (A,B)₂, ma il fatto è che esso, in virtù del II teorema di classificazione, rimane un prototipo per tutti gli altri continui di I specie numerabili (rammentiamo, senza minimo e senza massimo), che quindi al pari di lui debbono essere incompleti.

6. Sezioni di Dedekind e connessione*

E' venuto il momento di prestare qualche attenzione alla moderna analisi "aritmetizzante" della questione, e quindi dedichiamo questo paragrafo (più complesso dei precedenti) a Richard Dedekind, e all'opera Stetigkeit und irrationale Zahlen (Braunschweig, Vieweg & Sohn, 1872 - "Continuità e numeri irrazionali"). Riassumendo il suo punto di vista, e adattandolo alla nostra impostazione, dato uno spazio ordinato (X,w ), si possono andare a guardare le eventuali "decomposizioni" di X in coppie di sottoinsiemi non vuoti e disgiunti S' e S'' tali che: 1 - S' < S'' (con il che si intende che ogni elemento di S' è minore di un elemento di S''); 2 - S' non ha massimo, S'' non ha minimo; 3 - l'unione di S' e S'' è l'intero X (ne consegue che S' e S'' sono aperti nella topologia associata a w , e che ogni elemento minore di un elemento di S' è in S', non potendo essere in S''; analogamente, ogni elemento maggiore di un elemento di S'' è in S''). Una siffatta coppia ordinata (S',S'') di sottoinsiemi di X si dice una sezione di Dedekind di (X,w ) (S' è la classe inferiore della sezione, S'' la classe superiore), e diventa interessante studiare l'insieme delle sezioni di Dedekind di un assegnato spazio ordinato (X,w ), sinteticamente SD(X). [Un chiaro esempio di sezione di Dedekind appare nello spazio ordinato presentato dopo il teorema 2. Infatti l'insieme { A,S₁,S₂,...} costituisce la classe inferiore di una sezione, la cui classe superiore è individuata da { ...,R₂,R₁,B} .]

Sono evidenti i collegamenti con la condizione di completezza (C2). In effetti, se Y Í X è un sottoinsieme non vuoto superiormente limitato di X, privo però di estremo superiore, ecco che tutti i maggioranti di Y formano la classe superiore di una sezione di (X,w ); la classe inferiore è semplicemente il "complementare" di Mg(Y) in X (ossia, l'insieme di tutti gli elementi di X che non sono maggioranti di Y, vale a dire, che sono minori o uguali di qualche elemento di Y). Viceversa, se esiste una sezione di Dedekind (S',S'') di (X,w ), S' sarebbe un sottoinsieme non vuoto di X superiormente limitato ma senza estremo superiore (allo stesso modo, S'' sarebbe senza estremo inferiore). Insomma, non è difficile dimostrare che sussiste il seguente:

Teorema 6. Uno spazio ordinato è completo (soddisfa cioè la condizione (C2)) se, e soltanto se, non esistono sue sezioni di Dedekind: SD(X) = Æ .

In altre parole, la condizione SD(X) = Æ corrisponde a una nuova forma equivalente di (C2), oltre a (C2') e (C2''), che potremmo battezzare quindi (C2'''). Un continuo di II specie sarebbe, sotto questa prospettiva, un continuo di I specie privo di sezioni di Dedekind. Del resto, sono chiare pure le connessioni di (C2''') con il postulato di continuità della retta ordinaria orientata R. Infatti la nozione diciamo di classe inferiore di una sezione è riconducibile a una naturale "generalizzazione" del concetto di semiretta aperta: si tratterebbe di prendere in considerazione sottospazi senza massimo (e non vuoti) di uno spazio ordinato, tali che assieme a un dato elemento x contengano anche tutti gli elementi minori di x. Perché uno di essi sia una "semiretta vera" bisogna avere un suo "vertice", mentre la classe inferiore di una sezione, ammesso che ne esista una, vertice non può possederne. L'identità SD(R) = Æ , certamente vera, equivale ad affermare che non è possibile ripartire la retta in due semirette aperte: mancherebbe evidentemente il vertice comune (continuando ad avere in mente siffatte decomposizioni, R si può spezzare solo in una semiretta aperta e l'altra chiusa).

L'approccio di Dedekind consente alcuni sviluppi in effetti interessanti. Fissato un qualsiasi spazio ordinato (X,w ), è facile comprendere che l'insieme SD(X) "eredita" da (X,w ) una struttura d'ordine naturale, che rende quindi anch'esso uno spazio ordinato. Date due sezioni (supposte esistenti!), quella minore o uguale delle due avrà la classe inferiore contenuta nella classe inferiore dell'altra (parallelamente, la classe superiore conterrà l'altra classe superiore). Non solo, ma l'insieme X+SD(X) (il simbolo + ci sembra attualmente più suggestivo del simbolo di unione insiemistica È , perché si tratta di aggiungere letteralmente agli elementi di X degli elementi al di fuori di X: X e SD(X) sono sempre disgiunti) eredita dalla situazione una struttura di spazio ordinato naturale, bastando dire che un elemento x di X è minore (uguale non potrà essere mai!) di una sezione (S',S'') quando x Î S' [analogamente, x sarà maggiore di (S',S'') quando x Î S''].

A proposito del nuovo spazio ordinato X+SD(X), ci si persuade subito che valgono i seguenti:

Teorema 7. Se X è un continuo di I specie, X+SD(X) è ancora un continuo di I specie.

Teorema 8. X+SD(X) è sempre uno spazio ordinato completo [ossia: SD(X+SD(X)) =Æ ], che si può chiamare quindi il completamento di (X,w ) (in particolare, se X è già completo, SD(X) = Æ , e X+SD(X) = X, tutto torna).

Combinando i teoremi 7 e 8, si ottiene il:

Teorema 9. Se X è un continuo di I specie, X+SD(X) è addirittura un continuo di II specie.

Nota*. Si osservi che il precedente "completamento" non ha necessariamente la proprietà di essere in qualche senso "massimale". Per esempio l'intervallo aperto (0,1) in R è un continuo di II specie, ma è contenuto nell'intervallo chiuso [0,1], che risulta pure un continuo di II specie. Considerazioni di questo genere sono verosimilmente all'origine dell'accennata scelta della "compattezza" nella definizione corrente di "continuo topologico", una definizione che comunque rimane non convincente (torneremo sulla questione nel par. 8).

La nozione di decomposizione precedentemente introdotta permette una generalizzazione puramente topologica, che si dimostra di grande efficacia nel presente contesto. Fissato adesso un qualsiasi spazio topologico (X,t ), si dice una sua sconnessione una coppia (non serve ordinata) di aperti non vuoti X' e X'' di X tali che X = X'È X'' (in particolare, sia X' che X'' sono simultaneamente aperti e chiusi, quindi aperti e chiusi non vuoti, e diversi dall'intero X, è questa un'altra descrizione della sconnessione). Uno spazio che ammette delle sconnessioni si chiama sconnesso, e connesso in caso contrario. Ciò premesso, è chiaro allora che se uno spazio ordinato non è completo, possiede cioè delle sezioni di Dedekind, esso come spazio topologico è necessariamente sconnesso. L'affermazione si può anche "invertire", il che conduce al seguente:

Teorema 10. Uno spazio ordinato connesso (e si intende connesso rispetto alla topologia associata all'ordine) con almeno due elementi è necessariamente un continuo di II specie. Viceversa, un continuo di II specie è sempre connesso.

Dim. Se uno spazio ordinato (X,w ) è connesso, allora soddisfa certamente, come abbiamo detto, (C2'''), è cioè completo, ma soddisfa ovviamente anche (C1), se non è il vuoto o un singleton. Infatti se tra due elementi distinti x e y di X non ci fosse alcun altro elemento di X, avremmo manifestamente una sconnessione di X, individuata dalle due semirette aperte, e non vuote: (-¥ ,y) (che contiene x) e (x,+¥ ) (che contiene y). La seconda parte del teorema è più difficile: bisogna far vedere che, nelle ipotesi ammesse, non può esistere una sconnessione topologica di X, e per la dimostrazione rimandiamo a quella che segue il postulato PC5 nella citata http://www.dipmat.unipg.it/~bartocci/mat/continuit.doc (lì l'argomentazione viene condotta in relazione alla retta ordinaria R, ma il ragionamento si può ripetere tal quale per un qualsiasi continuo di II specie nell'attuale accezione).

Nota. Sottolineiamo che se l'incompletezza implica certamente la sconnessione, viceversa questa non implica l'incompletezza, come accade per esempio nel caso degli spazi ordinati discreti (oppure degli spazi illustrati nella prima figura del par. 4, che, ribadiamo, non sono connessi né nella qualità di sottospazi topologici della retta ordinaria orientata R, né in quella di sottospazi ordinati di essa). La sconnessione per uno spazio ordinato equivale soltanto al suo non essere un continuo di II specie.

Il trattamento della continuità proposto da Dedekind "filosoficamente" differisce alquanto dal nostro. Ad esso si conferisce il "merito" (che riteniamo in effetti assai dubbio) di evitare qualsiasi coinvolgimento di concetti geometrici. In particolare, considerato il campo dei numeri razionali Q (una struttura che appare invero lecito introdurre esclusivamente mediante considerazioni "aritmetiche"), con la sua naturale struttura d'ordine, ecco che siamo davanti a un continuo di I specie numerabile (privo di minimo e massimo), e quindi non completo (verità nota sin dagli albori della storia della matematica, senza fare ricorso al teorema 4). Quella di sezione di Dedekind di Q diventa così una "definizione", pretesa avulsa da ogni "intuizione geometrica", di numero reale irrazionale, e il completamento Q+SD(Q) viene identificato con la totalità dei numeri reali. Ossia si pone, per definizione: R = Q+SD(Q), "equazione" che costituisce l'essenza della cosiddetta aritmetizzazione dell'analisi²⁶ (tale insieme sostegno R eredita poi dalla situazione non solo una struttura d'ordine, ma anche una struttura algebrica, etc.), e con ciò chiudiamo questo paragrafo di "richiami".

Nota (importante). Vale la pena di sottolineare che l'idea di "sezione" si trova già ... in Euclide; né poteva essere altrimenti, dal momento che l'oggetto del pensiero che si sta descrivendo, cioè la retta geometrica R, è sempre lo stesso. In effetti un numero positivo "irrazionale" (a r r h t o V , secondo Platone e Aristotele: ineffabile, di cui non si può parlare, che non può essere de-finito), non è altro che la misura di un segmento ("libero") a di R rispetto a un segmento b , quando a non appartenga all'insieme (numerabile!) dei "multipli" dei "sottomultipli" di b (si tratta ovviamente dell'identica situazione illustrata mediante l'introduzione dell'insieme di punti W (A,B) nel par. 4). Data allora la coppia ordinata (a ,b ), l'insieme N´ N delle coppie ordinate di numeri naturali si ripartisce precisamente nell'insieme costituito dalle coppie (m,n) tali che ma < nb (i.e., il "numero razionale" n/m > a /b sta nella classe superiore della sezione "individuata" dal numero irrazionale a /b ), e dal suo complementare, ossia l'insieme delle coppie (m,n) tali che ma > nb (ma non potrà mai essere uguale a nb per ipotesi). La famosa quinta definizione del libro V degli Elementi (criticata da Galileo per la sua difficoltà, o "non adeguatezza", vedi http://www.dipmat.unipg.it/~bartocci/GAL.html) sta proprio a collegare la "misura" di a rispetto a b con la predetta sezione - mentre, viceversa, il fatto che ognuna di esse corrisponda a una misura non è che una banale conseguenza di (C2) (per la verità il caso inverso non è discusso esplicitamente in Euclide). In altre parole, i numeri reali secondo Euclide (la geometria greca, la geometria intuitiva perenne) non sono esattamente le sezioni, ma sono "isomorfi" alle sezioni, e l'autentica "origine" delle seconde rimane geometrica e non aritmetica [spazio e tempo naturalmente qui interagiscono, come del resto (quasi) sempre]. Che quella appena esposta non sia un'opinione "stravagante" di chi scrive è confermato dalla seguente osservazione (Sir Thomas L. Heath, The thirteen books of Euclid's Elements, Dover Publications Inc., New York, 1956, vol. II, p. 124), che dovrebbe essere tenuta nel giusto conto da chi pensa a queste cose, e a maggior ragione da chi le insegna: <<Max Simon remarks (Euclid und die sechs plamimetrischen Bücher, p. 110), after Zeuthen, that Euclid's definition of equal ratios is word for word the same as Weierstrass' definition of equal numbers. So far from agreeing in the usual view that the Greeks saw in the irrational no number, Simon thinks it is clear from Eucl. V that they possessed a notion of number in all its generality as clearly defined as, nay almost identical with, Weierstrass' conception of it. Certain it is that there is an exact correspondence, almost coincidence, between Euclid's definition of equal ratios and the modern theory of irrationals due to Dedekind>> (enfasi nel testo).

Nota*. L'occasione si presta a un breve cenno relativo al terzo approccio al problema del continuo citato nell'introduzione (dopo quelli insiemistico e topologico), che ha a che fare con la teoria dei campi ordinati. Ricordiamo che un campo K è una struttura algebrica con due operazioni, una somma e un prodotto, modellate sull'esempio del campo dei numeri razionali Q, e che un ordine in K si dice compatibile con la struttura algebrica se tanto la somma quanto il prodotto di elementi positivi (i.e., maggiori di zero) sono ancora elementi positivi. Bene, si vede subito che un campo ordinato K è necessariamente un continuo di I specie [tra due elementi x < y, esiste sempre l'elemento (x+y)/2; si noti che l'elemento unità 1 deve essere positivo, come ogni quadrato di K, e che quindi sono tutti positivi - in particolare mai nulli, come in un "campo astratto" potrebbe viceversa accadere - gli elementi 2 = 1+1, 3 = 1+1+1, etc.], e che il completamento di un siffatto campo ammette una struttura di campo ordinato, il quale sarà un continuo di II specie. [Si faccia però attenzione alla circostanza che la somma di due sezioni non è sempre una sezione: potrebbe "essere" un elemento di K, dal momento che la somma di due numeri irrazionali può ben risultare un numero razionale. Infatti, date (S'₁,S''₁) e (S'₂,S''₂), la coppia ordinata (S'₁+S'₂,S''₁+S''₂), con si spera manifesto significato dei simboli, è "quasi" una sezione di K, nel senso che se l'unione dei due insiemi in parola non è l'intero K, esiste comunque un unico elemento x Î K tale che questi insiemi coincidano con le due semirette aperte di vertice x. Analoga avvertenza per il prodotto, operazione che richiede peraltro qualche cura in più.] Di campi ordinati ne esistono molti, ma la loro varietà si riduce drasticamente quando si introduca il postulato di Archimede (cfr. nota 21), che nel presente caso si enuncia nel modo seguente: se x < y sono due elementi positivi di K, allora qualche multiplo intero nx di x supererà y (in una forma popolare: "a quattrino a quattrino si supera lo zecchino"). Il teorema di unicità nominato nell'introduzione ci informa che, a meno di isomorfismi (algebrici e d'ordine) esiste un solo campo ordinato completo archimedeo, che sarà isomorfo a R (potrebbe anche dirsi R per definizione, questo è il senso della "soluzione formalista" al problema della "natura degli enti matematici"), e quindi che ogni campo ordinato archimedeo è sostanzialmente un sottocampo di R. La precedente non è però un'illustrazione del continuo in termini di puro ordine, perché può accadere che due campi ordinati siano isomorfi come spazi ordinati, ma affatto differenti in quanto strutture algebriche ordinate: un campo può essere per esempio archimedeo, l'altro no (cioè, l'archimedeicità non è un "invariante d'ordine", non è una proprietà che si possa definire esclusivamente in termini di spazi ordinati). Si pensi al campo Q(p ), che viene chiamato l'estensione semplice di Q tramite il numero reale trascendente p (cfr. nota 23). Esso è formato dalle espressioni polinomiali del tipo a_np ⁿ+...+a_1p +a₀, con coefficienti numeri razionali (e certo non uguali a zero, a meno che tutti i coefficienti non siano zero), combinate insieme ai loro inversi. Nella veste di sottocampo di R, Q(p ), che dal punto di vista della teoria dell'ordine è un continuo di I specie numerabile, eredita un ordine archimedeo. Ma il medesimo campo risulta il sostegno di un ordine algebrico non archimedeo, che avrà l'effetto di produrre un "campo ordinato" completamente diverso dal precedente (il "sottocampo ordinato" di R), ma ad esso isomorfo nella categoria dell'ordine, poiché sempre con un continuo di I specie numerabile si avrà a che fare (e vale il II teorema di classificazione). Basta all'uopo definire positive [estendendo poi in modo naturale la definizione a ogni elemento di Q(p )] quelle espressioni polinomiali (non nulle) che hanno per "coefficiente direttore" a_n un numero razionale positivo. Le proprietà previste per un campo ordinato continuano a essere soddisfatte, ma è chiaro che risulterà p > n per ogni numero naturale n, ossia che, pur essendo 1 < p , nessun multiplo intero di 1 potrà mai superare p .

Nota*. Diviene interessante nell'attuale contesto determinare esplicitamente le sezioni di Dedekind di (A,B)₂, ciò che si effettua tramite particolari successioni di 0 e 1 (collegate alla numerazione in base 2, qualora si ponga: A = 0; B = 1; M = 1/2 = 0,1; M' = punto medio tra A e M = 1/4 = 0,01; etc.). Il risultato è che ogni successione di 0 e 1 che non consista da un certo punto in poi di tutti 0, o di tutti 1, individua univocamente una tale sezione, e viceversa ciascuna di queste si può rappresentare in detto modo (se 0001100101... è per esempio una delle successioni in parola, per decidere se M' sta nella classe inferiore o nella classe superiore della sezione associata, si va a guardare se 0,01 è minore o maggiore di 0,0001100101..., "scorrendo" le cifre da sinistra a destra - poiché la seconda cifra, dopo il primo ininfluente 0, associata al punto è 1, e la seconda di quella della sezione è 0, ecco che M' appartiene alla classe superiore, e così via). La descrizione rimanda più direttamente all'enunciato del II teorema di Cantor (vedi la nota 24), il quale stabilisce appunto che le nominate successioni formano una totalità più che numerabile. [Le successioni coinvolte nel ragionamento precedente sono in realtà solo una parte dell'intero insieme delle successioni, ma si dimostra che questo sottoinsieme è necessariamente equipotente al tutto. Ciò è conseguenza del fatto che le successioni escluse costituiscono palesemente un insieme numerabile, e che sussiste il seguente "facile" teorema: "Siano X, X' insiemi tali X Í X', X'-X sia al più numerabile, X' sia più che numerabile. Allora, non solo pure X è più che numerabile, ma X e X' hanno la stessa cardinalità".] Osserviamo ancora che l'incompletezza dei continui di I specie numerabile si può semplicemente provare senza il II teorema di classificazione, noto però il II teorema di Cantor, così argomentando. Sia (X,w ) un continuo di I specie numerabile, privo di minimo e massimo. Fissiamo arbitrariamente un elemento in X, e indichiamolo, per motivi che diventano ovvi tenuto conto di quanto spiegato sopra, con il simbolo 0,1 (0 virgola 1). Scegliamo poi un elemento alla sinistra e uno alla destra di 0,1, chiamandoli rispettivamente 0,01 e 0,11. Procediamo fino a determinare un sottospazio Y di (X,w ) che è isomorfo allo spazio di tutti i numeri razionali compresi strettamente tra 0 e 1, e con denominatore una potenza di 2. Una successione di 0 e di 1 del tipo dianzi indicato corrisponde a una sezione di Dedekind di Y, che non individuerà necessariamente una sezione di Dedekind di X (in X potrebbe esistere un elemento di separazione della sezione; vale pure a dire, "estesa" in maniera naturale per esempio da Y a X la classe inferiore di una di siffatte sezioni, in modo che continui a non avere massimo, il complementare di essa potrebbe però avere un minimo in X). Ma è chiaro che le sezioni di Y, e quindi le loro estensioni, sono "molte", in virtù appunto del II teorema di Cantor, laddove gli elementi di X sono per ipotesi "pochi", e cioè che esiste qualcuna delle sezioni in oggetto la cui estensione a X sarà ancora una sezione, ergo SD(X) ¹ Æ , c.v.d..

7. Il continuo di III specie e il continuo lineare

Ritornando alle nostre finalità definitorie, possiamo provare a rispondere ancora una volta alla domanda quale debba essere considerato il "vero" continuo. Abbiamo già visto che (C1) è una costituente essenziale della nozione di continuità, e che (C2) la integra opportunamente. Ma l'analisi non appare terminata, dal momento che un continuo di II specie non può dirsi un continuo lineare, il concetto che vorremmo invece riuscire a "definire". Infatti, con il continuo di II specie siamo lontani da un teorema di classificazione, o di "unicità" (si rammenti che pure il II teorema di classificazione era un teorema "parziale", limitato cioè al solo caso di spazi numerabili): esistono tanti continui di II specie non reciprocamente isomorfi, anche con lo stesso cardinale, e la loro totalità ha comunque cardinali crescenti (non può quindi asserirsi che il sostegno di un continuo di II specie ha necessariamente la "potenza del continuo", il termine che si usa per quella della retta ordinaria R, o dei numeri reali R)²⁷. Avendo in mente quanto accennato nella nota che chiudeva il par. 4, ai casi sopra menzionati di continui di II specie si possono aggiungere gli spazi ordinati Iⁿ, per ogni numero naturale n, dove con I designiamo l'intervallo chiuso [0,1] di R, e nell'insieme Iⁿ introduciamo l'ordinamento lessicografico. Si tratta di spazi ordinati che hanno il medesimo numero cardinale (la potenza del continuo), in virtù di un estremamente interessante risultato sull'infinito [cfr. ancora il teorema (V.38) nel cap. V delle "dispense"], ma non sono isomorfi per valori distinti della "dimensione" n. Come dire che dobbiamo sforzarci di trovare un'ulteriore proprietà caratteristica del continuo, e non essendo per fortuna tale impresa troppo difficile, ecco che saremo presto in grado di dichiararci finalmente soddisfatti.

L'osservazione dalla quale prenderemo le mosse per la scelta della definizione riguarda lo stretto collegamento che esiste tra un continuo di I specie numerabile ed R, la retta ordinaria orientata. Se è vero per esempio che W (A,B) non esaurisce la totalità dei punti di R, è pure vero che i punti di R non appartenenti ad W (A,B) sono almeno punti di accumulazione per elementi di W (A,B). Ossia, nella topologia naturale t di R, che è indotta dall'ordine, vale la circostanza che ogni intorno di P contiene qualche punto di W (A,B). Lo spazio topologico (R,t ) è quindi del tipo che in topologia si dice uno spazio topologico separabile (niente a che vedere però con l'attributo "separato" di cui alla nota 15), in quanto possiede un sottoinsieme numerabile Y tale che ciascun elemento di R sia un punto di accumulazione per Y. La retta, il piano, lo spazio ordinario, tutti gli spazi topologici Rⁿ (con l'ordinaria topologia che si chiama "prodotto", non con quella che deriverebbe dall'ordinamento lessicografico) per ogni numero naturale n, sono palesemente separabili. Ciò permette di introdurre la seguente nuova condizione:

(C3) Uno spazio ordinato si dice separabile quando è separabile la sua topologia d'ordine.

Ecco così che, proseguendo nella nostra analisi per restrizioni successive dell'idea di continuità, perveniamo alla definizione di continuo di III specie: uno spazio ordinato che soddisfa C1 + C2+ C3. Ovvero, riepilogando, uno spazio ordinato con almeno due elementi che sia ovunque non discreto, completo e separabile.

Per come abbiamo messo le cose, la retta ordinaria orientata R sarà un continuo di III specie, e tali tutti i suoi segmenti, o le semirette, aperte o chiuse. Per la nozione appena illustrata si trova l'auspicato teorema di classificazione (quasi un "teorema di unicità", di modo che il continuo di III specie appare il concetto che potrebbe denominarsi il continuo tout court, uso dal quale preferiremo però astenerci, almeno qui, al fine di evitare equivoci). Lo enunceremo, contrariamente al nostro solito, in una "veste numerica":

III Teorema di classificazione. Un continuo di III specie (X,w ) è isomorfo a uno e uno soltanto dei seguenti spazi ordinati, intervalli di R: [0,1], [0,1), (0,1], (0,1), a seconda che abbia rispettivamente massimo e minimo, abbia minimo ma non massimo, etc..

Corollario. In particolare, un continuo di III specie ha necessariamente la potenza del continuo. [Si rammenti la prima nota nel par. 2 di "Zenone".]

Dim*. Accenniamo alla dimostrazione, continuando a esaminare solo il caso che (X,w ) sia privo di minimo e di massimo. Sia dunque Y un sottoinsieme numerabile di X tale che ogni elemento di X sia un punto di accumulazione di Y, X Í D(Y). Y sarà anch'esso uno spazio ordinato senza minimo e senza massimo, anzi certamente un continuo di I specie (se esistessero due punti y' < y'' di Y con nessun punto di Y "in mezzo", allora gli infiniti punti di X che sono supposti comunque tra y' e y'' dovrebbero tutti essere in X-Y, e quindi avremmo punti di X con tutto un intorno disgiunto da Y, contro l'ipotesi che Y sia denso in X). Di conseguenza, in virtù del II teorema di classificazione, Y sarà isomorfo (d'ordine) a un qualsiasi altro continuo di I specie numerabile, in particolare a uno spazio ordinato Z che faccia le stesse veci di Y per (0,1). Possiamo pensare a Z proprio come all'insieme dei numeri razionali che hanno al denominatore una potenza di 2, cioè l'analogo numerico del D ₂(A,B) del par. 4, dove naturalmente 0 corrisponde ad A, e 1 a B. Quello che bisogna fare è cercare di estendere un isomorfismo f tra Y e Z a un isomorfismo tra X e (0,1), e la cosa non è difficile. Ogni elemento x di X-Y individua infatti manifestamente una sezione di Dedekind di Y, e ad essa rimane associata tramite f una sezione di Dedekind di Z, la quale sarà determinata da un ben preciso numero reale x compreso tra 0 e 1: è chiaro che si dovrà porre x = f(x) (ossia, l'estensione di f che stiamo cercando di determinare è univocamente definita dalla situazione).

Nota*. Non è vero però che gli unici continui di III specie di R, o di R, siano i suoi sottospazi topologici connessi. Per esempio lo spazio ordinato X = [0,1)È [2,3] in R è sconnesso, nella topologia dell'ordine di R, ma è manifestamente un continuo di III specie (l'estremo superiore dell'insieme [0,1) è il punto 2). Il fatto è che X risulta connesso nella sua propria topologia d'ordine (alla luce del precedente teorema, è isomorfo a [0,1]), e questo è uno di quei fenomeni a cui abbiamo accennato nella seconda nota presente nel par. 2. E' istruttivo cercare di comprendere bene che tutti gli intorni del punto 2, nella topologia d'ordine di X, contengono punti di [0,1), ossia [2,3] non è chiuso in X rispetto a tale topologia, mentre è chiuso rispetto alla topologia ereditata dall'ambiente.

Il III teorema di classificazione ha come conseguenza un altrettanto interessante "teorema di immersione", riferito ai soli continui di I specie (X,w ) che siano separabili, vale a dire, spazi ordinati soddisfacenti alle condizioni C1 + C2. Essendo chiaro infatti che il relativo spazio ordinato X+SD(X) è ancora separabile, e che risulta un continuo di II specie in virtù del teorema 9, ecco che X+SD(X) nelle attuali ipotesi è un continuo di III specie, d'onde il seguente:

Teorema d'immersione. Ogni continuo di I specie separabile è isomorfo a un sottospazio ordinato della retta ordinaria R.

Insomma, i continui di I specie separabili sono in qualche senso "spazi 1-dimensionali", in quanto possono essere immersi nella retta ordinaria orientata R. Ciò giustifica l'ultima definizione che proponiamo: si chiamino gli spazi ordinati del tipo in parola continui lineari (naturalmente, ogni continuo di I specie numerabile sarà un continuo lineare). Un siffatto spazio non è in generale completo (cioè, non è detto che sia di II specie, nel qual caso sarebbe allora, necessiter, di III specie), ma si potrà "rappresentare" come un qualsiasi sottoinsieme X di R, tale che tra due suoi punti ve ne siano sempre infiniti altri. Con questa nozione concludiamo la nostra ricerca definitoria nella categoria dell'ordine.

8. Insiemi e spazi topologici "continui"

Possiamo ripetere adesso alcune delle osservazioni già effettuate per il concetto di discreto, quando abbiamo analizzato le relazioni esistenti tra le tre categorie che qui giocano un ruolo fondamentale, degli spazi ordinati, degli spazi topologici, e degli insiemi. Nei paragrafi dedicati allo studio della continuità, assieme a ogni diversa nozione di essa, si è accompagnata una discussione topologica (la continuità di I specie è stata collegata alla densità, quella di II alla connessione, quella di III alla separabilità), che ci lascia modestamente soddisfatti sotto tale profilo. Continuiamo però a tenere bene in mente che la corrispondenza T di cui al par. 2 non è funtoriale, e che un generico spazio topologico, seppure denso in sé, o connesso, o separabile, non sarà in generale riconducibile a una struttura d'ordine, e che quindi non avrebbe senso, secondo il nostro punto di vista, porre la questione della sua eventuale "continuità". Ribadiamo inoltre che la denominazione corrente di spazio topologico continuo, la quale propone le due proprietà di compattezza e connessione²⁸, malgrado si comprendano le ragioni che la ispirano (e che la avvicinano alla continuità di II specie), rimane comunque "curiosa", perché esclude proprio la retta ordinaria R dall'ambito del continuo (se si preferisce l'approccio "numerico", l'insieme dei numeri reali R, inteso come spazio topologico, ovviamente con l'ordinaria topologia indotta dall'ordine naturale). Si tratta infatti di spazi topologici che non risultano compatti, nonostante sia piuttosto agevole "compattificarli".

Con riferimento al diagramma riportato nel par. 2, rimarrebbe da investigare una sensata definizione di insieme continuo, delle varie specie, e in tale contesto si ripresentano, è chiaro, le medesime alternative esaminate nel par. 3: definire un insieme X (infinito) continuo, di qualche specie, quando esiste uno spazio ordinato "al di sopra" di X che sia continuo, oppure quando tutti gli spazi ordinati sopra X siano continui. Si comprende subito che il secondo caso non si verifica mai: anche un semplice insieme numerabile è dotato di ordinamenti discreti, continui, oltre che né discreti né continui. Rimane quindi da percorrere unicamente la prima via, e la proposta più ragionevole da avanzare in proposito, conformemente peraltro alle "attese", è che un insieme X potrebbe dirsi un "continuo" (sottinteso per noi: di III specie) se e soltanto se ha la potenza del continuo, sed de hoc satis.

9. Conclusioni

Nel seguente diagramma viene sinteticamente delineato il duplice "fondamento intuitivo" della matematica secondo la nostra attuale impostazione, comprendente la genesi del concetto di "numero" (che si può sempre considerare il risultato di una misura, eventualmente "assoluta", vuoi operata su una retta discreta, vuoi su una retta continua). Maggiori delucidazioni riguardo allo schema si possono trovare nell'ultimo punto ("Un aggiornamento...") della citata pagina web delle "dispense".
 
 

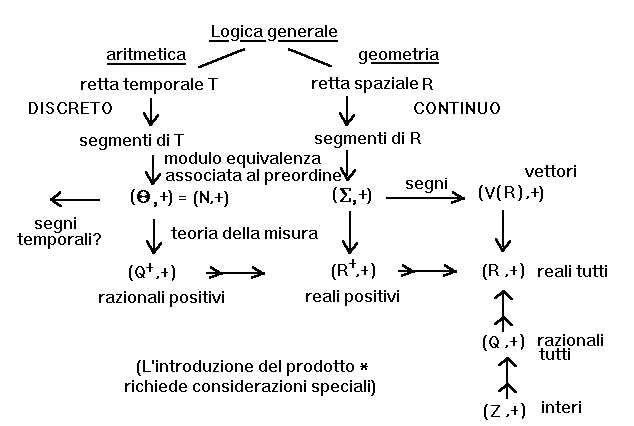
Torniamo proprio in fine d'opera sui paradossi che hanno ispirato questo lungo lavoro, esponendo concisamente, adesso che possiamo farlo nei termini matematici più appropriati, la soluzione (meglio: l'interpretazione) per essi proposta.

Per quel che concerne l'umana comprensione dello spazio e del tempo, l'intelletto è strutturato in modo tale da poter concepire l'esistenza e le proprietà di due "enti ideali" come la retta spaziale R e la retta temporale T. Spetta esclusivamente alla voluntas, mediante opera di "intuizione", di decidere quali siano gli enunciati maggiormente adeguati a descrivere R e T, un complesso di "verità" che sono dentro di noi e non fuori di noi (accertabili quindi per via di intuizione, non sperimentale). Con le dovute cautele, e facendo astrazione da altre specifiche caratteristiche, R e T possono riguardarsi come spazi ordinati, entrambi privi di minimo e massimo. Orbene, al di là delle ipotizzabili primitive intenzioni del loro autore, i paradossi costituiscono una sorta di "dimostrazione" perenne dei seguenti "teoremi".

Teorema 11. R e T sono spazi ordinati non isomorfi: il primo è un continuo di III specie, il secondo uno spazio discreto. In particolare, R e T non sono isomorfi neppure in quanto insiemi (totalità dei punti e totalità degli istanti non sono equipotenti). R e T continuerebbero a essere non isomorfi, vuoi come spazi ordinati che come insiemi, anche se T venisse concepito nella veste di continuo di I specie numerabile, ferma restando invece la precedente descrizione di R.

Teorema 12. Di conseguenza, il movimento, o il cambiamento, che sono aspetti indubitabili della realtà fenomenica, non possono essere "perfettamente" descritti mediante le due dette "forme pure" dell'intelletto, del resto le sole a nostra disposizione per tale scopo.

Teorema 13. I paradossi potrebbero continuare a essere formulati anche nell'ipotesi che R venisse considerato semplicemente un continuo di I specie numerabile, e a T fossero confermate le caratteristiche di spazio discreto. R e T sarebbero allora ancora non isomorfi come spazi ordinati, ma isomorfi come insiemi. Ossia, totalità dei punti e totalità degli istanti risulterebbero equipotenti, circostanza che non avrebbe comunque influenza sulla permanente impossibile riduzione delle due forme pure a una sola.
 
 

1 - Tali parole rimandano alla concezione della matematica che abbiamo in diverse occasioni illustrato, come una disciplina caratterizzata da un "divenire". Nella fase iniziale essa è "investigazione delle leggi dell'intelletto" (Investigation of the laws of thought è il titolo di una celebre opera di George Boole, 1854), in una successiva diviene "studio di tutte le possibilità di pensiero di una mente infinita" (secondo un'espressione del logico-matematico Gaisi Takeuti, citata da Rudy Rucker, Infinity and the Mind - The Science and Philosophy of the Infinite, Birkhäuser, 1982, Prefazione). Così, in conformità al principio per cui "l'ontogenesi ricapitola la filogenesi", nella formazione di un "matematico" (in senso generico, ciascun intelletto è in parte matematico; cfr. l'opinione di Frege citata più avanti nell'introduzione) bisognerà concedere tempo adeguato al primo momento.

2 - All'autore è stata rimproverata spesso un'eccessiva, e antipatica, vis polemica, ma non c'è nel fondo delle sue parole alcuna intenzione di denigrare altre persone reali (viventi): egli contesta principalmente se stesso, ciò che è stato, e ha per molti anni insegnato a essere, ciò che non sapeva pur credendo di sapere, ciò che non aveva capito pur credendo di capire. D'altronde, per diventare "professori", almeno nell'università italiana, e limitando il discorso alla matematica (ma è chiaro che il caso è generale), si è costretti a dimostrare di aver offerto contributi "originali" in qualche campo della disciplina. Il che è possibile, parlando genericamente, e data la moltitudine di docenti richiesta dall'odierna "università di massa", soltanto approfondendo argomenti astrusi e sostanzialmente inutili - dove qui inutile è inteso non solo con riferimento ad applicazioni pratiche, ma anche a quanto si deve poi di fatto insegnare, partendo necessariamente dalle premesse, e comunque indirizzando, volendo o non volendo, la mente (meglio: voluntas) degli studenti sulla maniera di trattare le questioni fondamentali. Soprattutto i giovani, quando sono chiamati a (de)formare gli esordienti, sanno poco o nulla di argomenti su cui hanno avuto scarso tempo per pensare, e non possono quindi che proporre un insegnamento passivo, non operando (non essendo in grado di operare) una scelta tra diverse definizioni, e ripetendo ciò che hanno sentito sommariamente raccontare in giro in ordine ai problemi fondazionali, in particolare quegli slogan citati dianzi. Ulteriore attenzione andrebbe concessa all'accennato tema dell'utilità, ossia al criterio con il quale deve essere valutata la rilevanza di una ricerca. Essa è in primo luogo personale, sviluppo della consapevolezza del ricercatore (termine che comprende chiunque), maturazione della cultura e della coscienza, che non si può programmare meccanicamente, né effettuare in difformità al principio "biologico" menzionato nella nota 1, ma una serie di ostacoli predisposti con perversa razionalità impediscono la realizzazione di quest'obiettivo. Aggiungiamo che, con invidiabile spirito di corpo, i matematici sosterrebbero oggi in modo pressoché unanime un'opinione contraria, enfatizzando (più o meno in buona fede, cioè strumentalmente, in periodo di predominio dell'homo oeconomicus) le ricadute pratiche della loro disciplina, e mettendo in evidenza, allo scopo di sottrarre le proprie attività da ogni forma di "giudizio", i rari esempi di indagini apparentemente lontane dalle "applicazioni" che si sono a posteriori rivelate fruttuose, confondendo però, e inducendo a confondere, l'eccezione con la regola.

3 - La medesima che probabilmente ispirò al celebre gruppo di matematici tedeschi composto da Weierstrass, Dedekind, Cantor, etc. il cosiddetto processo di aritmetizzazione dell'analisi nell'ultimo quarto del XIX secolo (vedi il par. 6). In ogni caso, una filosofia che di certo si affermò posteriormente, con una diffusione e consenso sconcertanti nella loro rapidità e universalità.

4 - Principles of Mathematics, 1903, da non confondersi con i successivi Principia Mathematica, scritti in collaborazione con Alfred North Whitehead, 1910-1913.

5 - Per esempio, si trovano ottimamente esposti nel libro di Joseph G. Rosenstein, Linear Orderings (Academic Press, New York-London, 1982) - si tratta delle stesse strutture che chiameremo qui "spazi ordinati". Opera che peraltro, a quel che ci sembra, non fa eccezione nel panorama illustrato, poiché non vi si troverebbero chiaramente enunciate (con le denominazioni appropriate) le definizioni di discreto e continuo che stiamo cercando (solo a p. 65 si nomina il continuo: <<the set R of real numbers, which he [Cantor, N.d.A..] called the continuum>>), anche se, naturalmente, le qualità matematiche che secondo noi caratterizzano tali concetti sono tutte nominate, sebbene con altri intenti. L'autore riconosce comunque la generale scarsa attenzione verso siffatte importanti strutture, esordendo con le parole: <<A book about linear orderings? You mean total orderings? What can you possibly say about them? After all, besides the natural numbers, the integers, the rationals, and the reals, what linear orderings are there? These questions, usually unspoken, were common. It is my hope that the reader will find this book a satisfactory response>>.

6 - Parafrasiamo qui un'azzeccata espressione di Aldo Spranzi, Anticritica dei Promessi Sposi, EGEA, Milano, 1995 (p. 830).

7 - L'autore prosegue a p. 149, dopo aver parlato di una <<necessità razionale, ma non logica in senso stretto>> (conseguenza della proposta dicotomia tra logica dell'intelletto e logica della ragione, vedi la nota 44 di "Zenone") che viene esplicata dal matematico nel corso di tale attività: << Da questi esempi si vede che l'arbitrio delle definizioni è sottomesso a criterii razionali di cui il matematico deve tener conto: la sua libertà, proprio come nella vita, implica responsabilità>>.

8* - E in ciò almeno siamo d'accordo con B. Russell, quando sostiene (loc. cit., cap. XXXII) che: <<la teoria della continuità è puramente ordinale>>. Si badi bene però che non si tratta della teoria dei cosiddetti numeri ordinali, ossia dello scheletro della categoria  (per maggiori informazioni: http://www.dipmat.unipg.it/~bartocci/mat/ord.doc), ma della categoria , o meglio, come qui la chiameremo,  (vedi la nota successiva). Uno spazio ordinato non è infatti, in generale, "bene ordinato", termine con cui si indicano quegli spazi ordinati (sigla ibo, insiemi, anziché spazi, bene ordinati) tali che ogni loro sottoinsieme non vuoto ammette un primo elemento. Nel contesto che più ci sta a cuore, se uno spazio ordinato discreto può essere a volte bene ordinato [i casi (i) e (ii) del successivo I teorema di classificazione], uno spazio ordinato continuo (di qualsiasi tipo) non può viceversa mai esserlo: tra il primo elemento e il secondo elemento non possono esistere altri elementi.

9 - Si richiede che una relazione d'ordine soddisfi alle naturali proprietà riflessiva (per ogni x: x £ x), transitiva (per ogni x, y, z: x £ y e y £ z, implica x £ z), e in più anti-simmetrica (se x £ y e y £ x, necessariamente x = y), una condizione quest'ultima che si può lasciar cadere, ma allora si preferisce parlare di preordine, anziché di ordine, ne offriremo un esempio tra breve. Il capitolo III delle citate "dispense" è dedicato alla nozione di relazione in generale, in esso però l'ordine totale, con evidente richiamo del resto alla sorgente intuitiva del concetto, viene detto ordine lineare (d'onde la denominazione di "insiemi linearmente ordinati", in luogo di spazi - sottinteso: totalmente - ordinati, e le sigle ilo per uno,  per la relativa "categoria"). Qui ci atterremo invece alla terminologia appena introdotta, riservando il termine "lineare" a una delle specificazioni del continuo (continuo di III specie), e proponendo la sigla  per la categoria in oggetto. Sottolineiamo ciò pur essendo ben consapevoli del fatto che osservazioni terminologiche di tale natura sono ritenute inutili, noiose, da parte di molti colleghi, ma è nostra opinione che trovare un nome (o un simbolo) "adeguato" sia al contrario estremamente importante. Per analogia, in fisica consideriamo assai istruttiva la scelta del sistema di unità di misura. Parecchi fisici sosterrebbero che si tratta di questione puramente convenzionale, che non deve interessare più di tanto, mentre le unità di misura "giuste" sono quelle coerenti con l'intima essenza della natura che si vuole descrivere (si veda nell'articolo "Etere e relatività", di Giuseppe Cannata, Episteme N. 2, la Tabella "Dimensioni e significati meccanici di alcune grandezze elettromagnetiche").

10 - Collegati evidentemente del resto alle uniche strutture su cui si fondi la costruzione dell'intero edificio matematico, secondo la progressione illustrata nella nota 1, più, se si vuole aggiungerlo esplicitamente, l'insieme vuoto, che si indica con il simbolo Æ .

11 - Per addentrarci ancora in questioni terminologiche, indichiamo in corsivo entità numeriche, quindi per esempio R per la totalità dei numeri reali, da non confondersi con l'R che designa la retta ordinaria. Per indicare i numeri reali tutti i matematici usano in effetti una sorta di lettera maiuscola "R" speciale, così comprendendosi al volo, mentre per la retta ordinaria non esiste alcun simbolo comune (per non dire del fatto che spesso il concetto non viene neppure introdotto!), il che la racconta lunga sugli effetti disastrosi della cancellazione dell'intuizione geometrica dai fondamenti della matematica, e dall'insegnamento. Nei corsi preliminari di "Geometria" si insegna oggi "Algebra Lineare" - attenzione ancora una volta ai nomi, poiché sono istruttivi - come se si potesse spiegare bene il significato della seconda senza fornire almeno dei rudimenti della prima.

12 - In verità, a ogni spazio ordinato si può associare lo spazio ordinato "opposto" (per esempio l'ordinamento associato a quello naturale in N è semplicemente: 1 > 2 > 3 >...), ma nel caso della retta R esistono due ordinamenti naturali, l'uno opposto dell'altro, che risultano però, come detto, tra loro assolutamente "indistinguibili".

13 - Non possiamo qui, per esigenze di brevità, neppure accennare a cosa sia uno spazio topologico. Basterà dire che si tratta di un insieme in cui sono distinti certi particolari sottoinsiemi, gli aperti, attraverso i quali si costruisce la nozione di intorno di un punto, e si può quindi procedere a operazioni di limite, verifiche di continuità, etc.. Per saperne di più, si veda per esempio l'"Interludio topologico" in http://www.dipmat.unipg.it/~bartocci/mat/continuit.doc.

14 - La differenza tra ordinamento e orientamento si percepisce solo in dimensione superiore a 1 [cfr. la nota (III.82) nel cap. III delle "dispense"], ma sulla non banale questione, un tradizionale pons asinorum per molti studenti di matematica, dobbiamo di necessità sorvolare.

15 - Una topologia che è manifestamente separata, cioè soddisfa l'assioma di separazione detto di Hausdorff: dati due qualsiasi punti distinti x e y di X, esistono un intorno U (dall'iniziale del tedesco Umgebung) di x e un intorno V di y che sono disgiunti, UÇ V = Æ. In effetti, (X,t_w) risulta addirittura quello che si chiama uno spazio di Tychonov, soddisfa cioè un assioma di separazione più "forte".

16* - Decidere se una topologia t ammetta o no un ordine dal quale sia indotta è un problema difficile, anche se t soddisfa la condizione necessaria deducibile dalla precedente nota (cioè, concesso a priori che t sia almeno una topologia separata). Diciamo qui soltanto che esistono ovvi esempi di topologie non indotte da ordini pure in spazi topologici separati, come il piano ordinario P (con la sua topologia naturale: una sottobase per gli aperti - anzi addirittura una base, per chi conosce questa distinzione - è costituita dall'interno dei cerchi di P). Infatti in una "topologia d'ordine" (termine il cui significato è ormai chiaro) l'eliminazione di un punto "sconnette" lo spazio (beninteso, se quello che rimane non è un singleton, o il vuoto, e se quello che si toglie non è l'eventuale minimo, o massimo, dello spazio), mentre ciò palesemente non accade in P. [Invece, un insieme finito possiede una sola topologia separata, coincidente con la topologia discreta, che nel presente caso è manifestamente una topologia d'ordine (verità peraltro di tipo generale). Su tali argomenti si ritornerà nel par. 3.]

17 - Si noti che in quest'ultimo caso, e soltanto in questo, non esiste un unico isomorfismo (o anti-isomorfismo) tra (X,w ) e il suo modello univocamente determinato dalla precedente "ripartizione" in famiglie, sostanzialmente perché Z, con il suo ordinamento naturale, è il solo tra gli spazi menzionati a essere dotato di automorfismi propri (sottinteso, in ), come si invita il lettore a "visualizzare" immediatamente senza "dimostrazione" formale (siamo dinnanzi a una situazione non geometrica in cui si presenta in modo naturale il fondamentale concetto di traslazione - traslazioni possono anche introdursi in N, ma allora non sono più corrispondenze biunivoche).

18 - Certo, a meno che non si intenda il "continuo" in un'accezione "forte", per esempio quella che chiameremo continuo di II specie, con l'effetto che uno spazio ordinato numerabile non potrà mai essere un continuo in tale senso (vedi teorema 4).

19* - La dimostrazione è in effetti piuttosto semplice. Sia X un sottoinsieme di P composto da tutti punti isolati: per ogni punto x di X, almeno un aperto U di P soddisferà la condizione
UÇ X = { x} . Poiché P ammette una base numerabile per gli aperti, chiamata Y una di esse, possiamo supporre che U sia un elemento di Y . Considerato il sottoinsieme Y ' Í Y di tali aperti U, è chiaro che abbiamo a che fare con una corrispondenza f : Y ' ® X, che manda ogni elemento U del dominio nel punto x Î X di cui sopra. La corrispondenza risulta suriettiva per ipotesi, sicché esisterà senz'altro, in virtù del cosiddetto "assioma della scelta" (vedi la già citata appendice al cap. III delle "dispense"), una funzione iniettiva X ® Y ' che "inverte" (a sinistra) la precedente. Ne consegue che X è equipotente a un sottoinsieme di Y ', che per ipotesi era numerabile, e quindi che X è finito o al più numerabile.

20 - Si noti che il derivato D(X') fa riferimento alla topologia t di X, e che in qualche caso è bene riportare esplicitamente t in D(X'), cioè scrivere qualcosa del tipo Dt (X'), qualora si debbano chiamare simultaneamente in causa diverse topologie, e sia opportuno evitare equivoci. Per esempio, abbiamo detto che un sottospazio X' Í X è denso in sé se X' Í D(X'), il che significa a rigore X' Í Dt (X'). Se t ' indica la topologia indotta da t su X', possiamo anche introdurre il derivato Dt _'(X'), per il quale risulterà manifestamente Dt _'(X') = Dt _'(X')Ç X'. Si capisce allora subito che supporre X' Í Dt (X') è la stessa cosa che supporre X' Í Dt _'(X'), come era auspicabile.

21 - Il postulato di Archimede, cui si faceva cenno nell'introduzione, equivale ad affermare che l'unione di tutti i segmenti individuati da due vertici consecutivi di D (A,B), o di D ₂(A,B), etc., coincide con l'intera retta.

22 - Mentre la verità di tale asserzione è immediata per W ₂(A,B), W ₃(A,B), etc., lo è meno per W (A,B). E' chiaro che qui si ha a che fare con la "necessità" di coppie di segmenti tra loro incommensurabili, ovvero con il concetto di numero reale irrazionale, dal momento che un punto C della retta R sta in W (A,B) oppure no a seconda che il segmento  abbia o non abbia misura razionale (esprimibile mediante il rapporto di due numeri naturali) rispetto al segmento . La consapevolezza dell'esistenza di questi punti C in R, comunque fissati A e B (cioè, della circostanza che il complementare di W (A,B) in R non può essere concepito uguale al vuoto), è presente sin dai primordi della matematica greca (e pare solo della matematica di quella civiltà), sicché la possiamo dare anche noi per acquisita.

23 - E' questo un ulteriore esempio di quanto osservato in "Zenone" (fine del par. 4), a proposito dell'assoluta naturalezza di considerazioni preliminari intorno a concetti quali "limite" etc.. Già Archimede, nel III secolo AC, applicando tali ragionamenti, fu in grado di collocare p  nell'intervallo tra 223/71 e 22/7 (senza che coincidesse con alcuno degli estremi), il che equivale a determinare esattamente le prime tre cifre decimali del famoso e difficile "numero" in questione. Aggiungiamo che unicamente nel 1770 si riuscì a provarne l'irrazionalità, con Johann Heinrich Lambert, mediante considerazioni di calcolo infinitesimale, mentre bisognerà aspettare il 1882 per dimostrarne, grazie a Ferdinand Lindemann, la trascendenza. Come dire che della sporadica esistenza di qualche numero trascendente si viene edotti soltanto assai tardi nella storia della matematica, tra l'altro in seguito ad argomentazioni piuttosto complesse, laddove quasi negli stessi anni è Cantor che persuade d'un colpo della "necessità" di un insieme infinito di numeri trascendenti, addirittura non numerabile (vedi anche la nota inserita più avanti nel presente paragrafo). Rimane comunque il fatto che decidere in generale se un singolo dato numero reale sia o no trascendente è impresa estremamente ardua.

24 - Diciamo conseguenza perché preferiamo enunciare il II teorema di Cantor nella seguente forma: così come la totalità P(X) (insieme delle "parti" di X) dei sottoinsiemi di X è "più grande" di X nel caso di un insieme finito, ciò continua a essere vero anche per N, ossia N e P(N) non si possono mettere in corrispondenza biunivoca tra loro (che P(X) sia sempre non inferiore a X è circostanza evidente). Ovvero, con il linguaggio espressivo che abbiamo spesso usato, N e P(N) non hanno la stessa "potenza", non sono "equipotenti". L'affermazione in parola può anzi estendersi a ogni insieme infinito X, e questo è l'oggetto del cosiddetto II teorema di Cantor-Bernstein, per cui rimandiamo ancora una volta al capitolo V delle "dispense", teorema (V.36). La dimostrazione del teorema si risolve poi in un ragionamento relativo alla totalità delle successioni di 0 e 1, le quali corrispondono biunivocamente ai sottoinsiemi di N [cfr. il teorema (I.91) nel I cap. delle "dispense"]. Siamo qui nel cuore dell'analisi cantoriana del concetto di infinito, senz'altro una delle creazioni più originali, e significative (cioè, pure da un punto di vista filosofico) della matematica del XIX secolo.

25 - Nella citata pagina http://www.dipmat.unipg.it/~bartocci/mat/continuit.doc (dimostrazione del teorema (11-5-1)) si dà un'altra dimostrazione diretta di tale enunciato, che non "passa" cioè per il II teorema di Cantor, mediante successive tricotomie. La si è desunta da Giuseppe Scorza Dragoni, nostro professore di Analisi Matematica a Roma: Elementi di Analisi Matematica, 3 voll., Ed. Cedam, Padova, 1961; II ed. 1963, vol. I, pp. 77-79. In quest'opera (vol. II, p. 16 e p. 30) viene chiamato "continuo" un sottoinsieme di uno spazio Rⁿ che sia chiuso e connesso. La definizione (puramente topologica) possiede il merito di evitare le incongruenze relative alla compattezza di cui si dirà nel par. 8, ma ha il difetto di non essere "invariante per omeomorfismi". Per esempio, (-¥ ,0] e (0,1] sono spazi topologici omeomorfi, però il primo costituirebbe un continuo di R, il secondo no (la definizione risulta ovviamente invariante solo per auto-omeomorfismi dello spazio ambiente Rⁿ).

26 - Citiamo l'opinione dello stesso Dedekind (nella traduzione di Oscar Zariski): <<Le ultime parole illuminano chiaramente la via per la quale si può giungere a un campo continuo ampliando il campo discontinuo R dei numeri razionali>>. Siamo di fronte a un limpido esempio di quanto un differente "atteggiamento filosofico" possa influenzare la descrizione dei medesimi "fatti" matematici. Per noi il campo dei numeri razionali (che indichiamo con Q, e non con R) non è "discontinuo", bensì continuo, seppure soltanto di I specie (Q è numerabile, perciò incompleto, ossia non è un continuo di II specie, in conseguenza del teorema 4). Aggiungiamo l'informazione che nel sito:
http://www.geometry.net/detail/math_discover/dedekind_cuts_page_no_4.html si può trovare l'usuale interpretazione del lavoro del matematico tedesco: <<In the introduction to this paper he points out that the real number system can be developed from the natural numbers: "I see the whole of arithmetic as a necessary, or at least a natural, consequence of the simplest arithmetical act, of counting, and counting is nothing other that the successive creation of the infinite sequence of positive whole numbers in which each individual is defined in terms of the preceding one">>. Quest'unica "intuizione discreta" (tale è manifestamente il passaggio al "successivo"), cioè l'iterazione, sarebbe dunque a fondamento del continuo geometrico, esattamente l'opinione criticata nell'introduzione. Sottolineiamo che rimane però vero, ma è un risultato appunto "banale", che i numeri razionali (positivi), e quindi un continuo di I specie, si possono dedurre dalla retta temporale discreta T, semplicemente quali prodotto dell'operazione di misura tra coppie ordinate di segmenti di T, anche se esiste per essi la possibilità di una misura assoluta (rispetto al segmento minimo), che fornisce esclusivamente dei numeri "interi" (naturali) - si rammenti la seconda nota del par. 5 di "Zenone". Insomma, i numeri razionali scaturiscono in maniera "spontanea" due volte, una da T e una da R, nel secondo ambiente come un caso particolare (cfr. l'inizio del par. 9). L'immersione dei numeri razionali di origine temporale nei numeri reali tutti di origine spaziale corrisponde palesemente all'immersione messa in evidenza nella seconda nota del par. 4: ribadiamo che si tratta di una circostanza che non giustifica alcun tentativo di riduzione, in nessuno dei due versi.

27* - Possiamo trovare esempi di continui di III specie anche in cardinalità superiori, per di più indefinitamente crescenti. Si prendano le mosse dagli spazi ordinati Rⁿ citati nell'ultima nota del par. 4, e vi si ponga all'esponente, in luogo del numero naturale n, un qualsiasi numero ordinale a . Come si sa, Ra può considerarsi uno spazio di funzioni del tipo A ® R, dove A sia uno spazio bene ordinato rappresentante l'ordinale a . L'ordinamento lessicografico in questo spazio funzionale rimane definito nel seguente modo: per ogni coppia ordinata di funzioni f e g, supposto che sia f ¹ g, si introduce l'insieme non vuoto degli elementi x Î A tali che f(x) ¹ g(x), e se ne considera il minimo elemento y (certo esistente per l'ipotesi di buon ordinamento): si stabilisce quindi che è f < g se f(y) < g(y). E' chiaro che, rispetto all'ordine in oggetto, Ra è sicuramente un continuo di I specie, e che di conseguenza il suo completamento, ai sensi del teorema 9, è un continuo di II specie del tipo ricercato.

28 - C'è chi aggiunge alla due citate condizioni quella che lo spazio topologico sia metrizzabile. Ciò ha l'effetto non solo che diverse nozioni di compattezza vengono a coincidere, ma anche che, poiché uno spazio compatto e metrizzabile risulta certamente separabile, uno spazio topologico che sia "continuo" in tale senso ha necessariamente la potenza del continuo, e questa è una circostanza interessante, con riferimento a quanto si dirà tra breve, alla fine del paragrafo.
 
 

[Richard Dedekind nacque a Braunschweig (Brunswick), come Carl Friedrich Gauss, che vi aveva avuto i natali nel 1777. Iniziò i suoi studi all'università di Göttingen nel 1850, dove fu uno degli ultimi pupilli del  Fürst der Mathematiker (Princeps mathematicorum), che morì nel 1855. Proprio con Gauss si addottorò nel 1852, e rimase a insegnare e a studiare a Göttingen quando alla morte del maestro Peter Gustav Lejeune Dirichlet ne prese il posto. Divenne professore a Zurigo nel 1858, ritornò a Braunschweig nel 1862, quale docente al Politecnico, e ivi rimase tranquillamente fino al termine della vita. Questi dettagli biografici sembrano un'ulteriore conferma dell'influenza filosofica, secondo noi "nefasta", che il <<sommo geometra>> esercitò su tutti (o quasi: per esempio non pare che Cantor abbia mai avuto legami diretti con Göttingen, a parte l'amicizia personale con Dedekind) i "rifondatori" tedeschi della matematica nella seconda metà dell'Ottocento (si veda in Episteme N. 6, Parte II, lo splendido Gaussbuster composto da Rocco Vittorio Macrì per il suo "Neopitagorismo e Relatività").]
 
 

Ringraziamenti. L'autore menziona con riconoscenza i colleghi Alessandro Caterino, Sauro Tulipani, Maria Cristina Vipera e Paolo Zappa, per le stimolanti discussioni e suggerimenti ricevuti nel corso della stesura dell'articolo (alla terza si debbono in particolare la dimostrazione di cui alla nota successiva al teorema 1, e il ragionamento che chiude la nota inserita alla fine del par. 6; al quarto la semplice dimostrazione qui proposta del II teorema di classificazione).
 

[Una presentazione dell'autore si trova nel numero 1 di Episteme.]

bartocci@dipmat.unipg.it