E' stato scritto che:

<<Dei sette paradossi, a noi pervenuti, che la tradizione attribuisce a Zenone di Elea¹ [...], quattro riguardano il movimento e sono stati oggetto di indagini profonde in tutti i tempi, dirette a comprenderne l'autentico, originario significato: indagini ardue e mai concluse, che ogni generazione di filosofi e matematici suole riprendere>>².

L'attuale generazione non fa naturalmente eccezione alla regola. Per esempio, ancora recentemente è apparsa su Le Scienze³ la notizia di una definitiva soluzione dei paradossi grazie a "caratteristiche fondamentali" di "nuove teorie matematiche":

<<Per due millenni e mezzo i paradossi di Zenone sono stati fonte di discussione e oggetto di analisi, ma solo oggi, grazie a una formulazione dell'analisi matematica che è stata sviluppata nell'ultimo decennio, è possibile risolverli [...] Per molti secoli la logica di Zenone è rimasta pressoché intatta, e ciò dimostra la tenacia dei suoi argomenti>> (p. 60, p. 66).

A proposito della pretesa "soluzione" in oggetto preferiamo astenerci da un giudizio circostanziato: diciamo solamente di avere l'impressione che tali affermazioni possano essere ricondotte a quello stato di confusione mentale e di presunzione di cui sono responsabili le pessime filosofie della matematica e della fisica del XX secolo⁴. Sottolineiamo piuttosto come l'asserzione in esordio sia eccessivamente restrittiva per ciò che concerne le finalità di dette costanti riprese: infatti, non si tratta soltanto di ricostruire l'originario significato, le esatte motivazioni, di un dibattito ormai lontano da noi nei secoli, cioè di studi in una parola filologici, quanto di analizzare in che misura gli argomenti di Zenone d'Elea siano, oggi al pari di ieri, una sorta di punto di passaggio obbligato verso una comprensione dell'umana concezione dello spazio e del tempo. In altre parole, al di là dell'indubbio interesse che gli argomenti della filosofia eleatica contro il movimento rivestono per la storia del pensiero greco (e della civiltà occidentale che da quello si sviluppò), si ricerca pure, come si diceva dianzi, una "soluzione" dei paradossi. Per tornare al caso di cui sopra, il lavoro di McLaughlin a tale mèta aspira, pertanto sotto questo profilo almeno esso è apprezzabile⁵.

Il presente articolo si colloca sulla medesima scia propositiva, sebbene con un'impostazione, come si vedrà, affatto differente. Per riassumere brevemente la nostra opinione, alquanto "tradizionale" e non "moderna": spazio e tempo, "forme pure" dell'intelletto secondo l'analisi critica kantiana, sono appunto due, e non una, apparentate alle intuizioni non solo diverse ma addirittura "contrapposte" (termine di cui si comprenderà meglio il significato precipuo nell'annessa appendice matematica, che è parte integrante di questo saggio), che si dicono comunemente del continuo e del discreto⁶. I paradossi di Zenone sono atti a convincerci precisamente di tale irriducibile, insormontabile dualismo (che potrebbe aggiungersi alle quattro antinomie kantiane della ragione pura⁷). Inoltre, anche di un altro fondamentale dualismo costringono a tenere conto: quello tra reale e pensato⁸, che in termini kantiani si esprime con i concetti di fenomeno e noumeno, e in termini cartesiani di res cogitans di res extensa (di un ulteriore profondo e collegato dualismo, presente sullo sfondo di questi discorsi, diremo più avanti, nel paragrafo 7).

Svilupperemo tale intento senza alcuna pretesa di nemmeno citare i più importanti studi sull'argomento, sia che essi abbiano finalità della prima categoria sopra descritta, sia della seconda (o siano, per così dire, "misti", in diverse percentuali): la bibliografia sarebbe invero sterminata. Ci limiteremo ad appoggiare i nostri ragionamenti su ciò che meglio si presterà di volta in volta a illustrare l'interpretazione che vogliamo proporre.

2. La formulazione dei paradossi secondo la tradizione più autorevole

Cominciamo a prendere le mosse da Aristotele (Fisica, VI, 9), ricordando come egli descriva i primi due paradossi, gli unici di cui qui ci occuperemo, al punto che quando diremo "i paradossi di Zenone", qui e nell'appendice, intenderemo fare riferimento solo a questi due (sfioreremo appena il terzo nel paragrafo 9, e ancora meno il quarto nella seconda nota del medesimo paragrafo), nella convinzione che si tratti poi "sostanzialmente" di uno soltanto, almeno a posteriori (rammentiamo che nessuno ci è pervenuto nella forma originale nella quale fu enunciato dallo stesso Zenone, neppure in maniera frammentaria, bensì esclusivamente attraverso siffatti commenti "di seconda mano").

<<Quattro sono i ragionamenti di Zenone intorno al movimento, i quali mettono di cattivo umore quelli che tentano di risolverli. Primo è quello sulla inesistenza del movimento, per la ragione che il mosso deve giungere prima alla metà che non al termine>>.

Siamo davanti alla cosiddetta dicotomia, ovvero a un'applicazione del principio geometrico secondo cui sulla retta ordinaria, tra due punti A e B, si concepisce, si "deve" concepire, un (unico) punto medio M. Con la conseguenza che, iterando l'applicazione del principio (l'iterazione è una delle funzioni logiche fondamentali dell'intelletto), tra A e M si deve successivamente concepire un nuovo punto medio M', e così via, all'infinito - o, se si preferisce un trattamento solo "potenziale": senza che nessun passo delle progressive iterazioni possa configurarsi quale ultimo, poiché tra due punti distinti deve esistere sempre un punto medio, e tutti i punti della successione A, M, M', ... sono certamente distinti.

Non ce ne sarebbe bisogno, ma espandiamo un poco quanto viene così sinteticamente riferito da Aristotele. Se vogliamo immaginare (o descrivere) un movimento da A verso B, due punti distinti della retta ordinaria⁹, dovremo prima di tutto pensare, secondo Zenone, a un movimento da A verso M, il punto medio del segmento di estremi A e B. Ma prima di questo a un movimento da A verso M', etc., con l'effetto che il punto A non può apparentemente neppure "cominciare" a muoversi - sottinteso: nella nostra mente.

Nota. Tra due punti distinti A e B della retta ordinaria R, comunque "vicini", risulta quindi necessario concepirne infiniti. In effetti, un semplice ragionamento mostra addirittura che i punti tra A e B devono essere concepiti "tanti quanti" quelli sull'intera retta (cioè, i due insiemi sono come si dice equipotenti, d'onde il termine potenza per indicare la "quantità" degli elementi di un insieme). Nella seguente figura viene illustrata una corrispondenza biunivoca che trasforma un punto p, interno al segmento  di estremi a e b, in un punto p' di R (si tenga presente che in questa nota A e B, e in generale tutti i punti, saranno indicati, differentemente dal solito, con lettere minuscole).
 
 

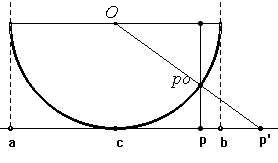
Per il punto medio c di  si costruisce la semicirconferenza tangente C, di centro O, riportata in figura, iscritta al quadrato di lato . Poi, dato un qualsiasi punto p all'interno del segmento, si determina il punto p₀ su C, situato su C e sulla retta verticale uscente da p. Infine, si costruisce p' Î R come illustrato, quale intersezione di R con la retta passante per O e per p₀. E' evidente che, al variare di p all'interno di , il corrispondente punto p' descrive tutti i punti di R, ciascuno una volta sola (in particolare, c' = c; i punti tra c e b, b escluso, corrispondono a tutti quelli alla destra di c, secondo la figura, mentre i punti tra a e c, a escluso, a quelli alla sinistra di c). Abbiamo asserito che questo ragionamento è assai semplice. A chi volesse rilevare un anacronismo, obiettando che diventa tale soltanto con il senno del poi, vale a dire dopo i noti sviluppi dell'analisi cantoriana del concetto di infinito, replicheremmo che non sono tanto gli alti livelli raggiunti da certa matematica di fine ottocento a stupirci, quanto piuttosto la precedente arretratezza.

Il paradosso dell'Achille è invece così descritto dal grande filosofo di Stagira¹⁰:

<<Secondo è l'argomento detto Achille. Questo sostiene che il più lento non sarà mai raggiunto nella sua corsa dal più veloce. Infatti è necessario che chi insegue giunga in precedenza là di dove si mosse chi fugge, di modo che necessariamente il più lento avrà sempre un qualche vantaggio. Questo ragionamento è lo stesso di quello della dicotomia, ma ne differisce per il fatto che la grandezza successivamente assunta non viene divisa per due. Dunque il ragionamento ha per conseguenza che il più lento non viene raggiunto ed ha lo stesso fondamento della dicotomia (infatti la conclusione di entrambi i ragionamenti è che non si arriva al termine, divisa che si sia in qualche modo la grandezza data; ma c'è di più nel secondo, che la cosa non può essere realizzata neppure dal più veloce corridore immaginato drammaticamente nell'inseguimento del più lento), di modo che la soluzione sarà, per forza, la stessa>>.

Nella Fisica di Simplicio (commentatore delle opere di Aristotele vissuto nel VI secolo DC), la questione dell'Achille è riferita invece con le seguenti parole:

<<Anche questo argomento basa la sua tentata dimostrazione sulla divisibilità infinita, ma è svolto in maniera diversa. Esso procede come segue: se esistesse il movimento il più lento non potrebbe mai essere raggiunto dal più veloce: ma questo è impossibile pertanto il moto non esiste. [...] L'argomento è chiamato l'Achille a causa dell'introduzione in esso di Achille, il quale, dice l'argomento, non può mai raggiungere la tartaruga che sta inseguendo, perché l'inseguitore deve, prima di raggiungere l'inseguito, giungere al punto dal quale l'inseguitore è partito. Ma nel tempo impiegato dall'inseguitore per raggiungere questo punto, l'inseguito avanza di una certa distanza e anche se questa distanza è minore di quella coperta dall'inseguitore, a cagione del fatto che l'inseguito è il più lento dei due, ciò nonostante egli avanza perché non è fermo. E ancora nel tempo che l'inseguitore impiega per coprire questa distanza di cui l'inseguito è avanzato, l'inseguito ancora avanza di una certa distanza che è in proporzione più piccola della precedente, in conformità al fatto che la sua velocità è minore di quella dell'inseguitore. E così in ogni intervallo di tempo nel quale l'inseguitore copre la distanza di cui l'inseguito, movendosi alla sua velocità relativamente minore, è avanzato, l'inseguito avanza ancora un altro poco, perché benché questa distanza decresca ad ogni passo, pure, a cagione del fatto che l'inseguito è sempre supposto in moto, egli avanza di qualche distanza positiva. E così considerando distanze decrescenti in una data proporzione all'infinito a causa dell'infinita divisibilità delle grandezze, arriviamo alla conclusione che non solo Ettore non sarà mai raggiunto da Achille, ma neppure la tartaruga>>.

Si vede di qui che già i due citati commentatori di Zenone avevano ben chiara l'essenza del dilemma, ovvero il principio geometrico del quale esso era conseguenza: quello dell'infinita suddivisibilità delle grandezze¹¹. E' l'applicazione di detto principio (che potrebbe limitarsi soltanto alla divisione per due, cioè alla dicotomia) non solo alla retta, dove si pensa avvenga il movimento, ma anche al tempo, in cui il movimento oggetto di attenzione si svolge, la chiave di tutto.

Nota. Ci sembra istruttivo un cenno alle ragioni che convincono della possibilità di suddividere un segmento fissato in un qualsivoglia dato numero intero (positivo) n di parti (in quel che segue esamineremo il caso n = 3, ossia la tricotomia). Esse si basano, come spesso avviene in simili frangenti, su argomentazioni di geometria piana (si immerge la retta nel piano che diremo pur esso ordinario), le quali coinvolgono l'esistenza e le proprietà delle rette parallele. Il parallelismo appare, una volta di più, uno dei fondamenti essenziali di ogni discussione geometrica.
 
 

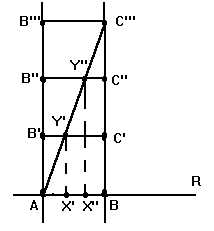
Nella figura si considera un segmento  della retta ordinaria R (pensata immersa nel piano ordinario P come una sua retta arbitraria). Dal punto A si traccia la perpendicolare alla retta R, e su tale perpendicolare si considera il segmento  uguale ad . Quindi lo si riporta di seguito tre volte, costruendo i segmenti , , . Sulla retta perpendicolare ad R nel punto B si considerano i punti C', C'', C''', corrispondenti rispettivamente di B', B'', B''' per proiezione perpendicolare. Si prende infine in esame la diagonale  del rettangolo ABB'''C'''. Essa interseca il segmento nel punto Y', il segmento  nel punto Y'', e le proiezioni perpendicolari di tali punti sulla retta R, che abbiamo detto rispettivamente X' e X'', forniscono la desiderata tricotomia del segmento , ossia:  =  = , e ++ = . Insomma, se sull'asse perpendicolare si rappresenta il numero intero n, su quello di partenza appare il suo inverso 1/n.

3. Il dualismo res extensa/res cogitans, oppure reale/pensato¹²

Sgombriamo prima di tutto il campo da "soluzioni" del tipo di quella data da Henri Bergson in Essai sur les données immediates de la conscience (il saggio con cui il filosofo si addottorò nel 1889). Quegli ritenne infatti che bastasse osservare:

<<l'errore zenoniano consiste nell'aver ammessa divisibile l'unità di movimento che, nel caso, dovrebbe corrispondere alla misura del passo di Achille: il quale, quindi, trovandosi, ad esempio, a mezzo passo dalla tartaruga con un intero suo passo certamente la sorpasserebbe>>.

E' chiaro che detta soluzione ha qualche valore, anche secondo il punto di vista che faremo nostro, giacché introduce nella discussione una sorta di "quantizzazione", in relazione al "passo" di Achille. Allo scorrere del tempo, Achille percorre via via un numero intero di passi, sicché a un certo punto sicuramente supera la tartaruga. Da tale prospettiva, l'obiezione zenoniana non può neppure formularsi, perché a detti enti non può applicarsi il principio dell'infinita suddivisibilit๳. E' pure chiaro, però, che la soluzione indicata utilizza il dualismo tra reale e pensato, dipanando il dilemma quando esso sia portato sul piano del reale. Quindi, in verità, vi si confonde lo spazio fisico (reale) con lo spazio "immaginario" (pensato)¹⁴. Il movimento, il continuo mutare eracliteo della realtà sotto gli occhi di qualsiasi essere umano, è un indubitabile dato di comune e costante esperienza, e in questo senso va interpretata la celebre "risposta" a Zenone che la tradizione attribuisce al cinico Diogene di Sinope (secondo le Vite e dottrine dei filosofi di Diogene Laerzio¹⁵). Ma quella di Zenone va riguardata come una pura argomentazione del pensiero: si possono infatti immaginare punti ideali in movimento (la cui posizione varia cioè nel tempo, il tempo dell'osservatore pensante) su una retta ideale, non corpi materiali in moto su un percorso reale. Perciò, si può ben supporre di descrivere "l'inseguimento" (o almeno parte di esso) suddividendolo in una successione ("discreta") di segmenti distinti tra di loro. Vale a dire che si può concepire un punto A (Achille) che si porta, in un certo tempo t , in un punto T (la tartaruga), di modo che A si trova in A' = T, mentre, nello stesso tempo t , T si è spostato in un altro punto T' (il rapporto tra i due segmenti  e  è precisamente il rapporto, supposto maggiore di 1, tra le due velocità, quella di Achille e quella della tartaruga, i cui moti si suppongono uniformi). Poi, si può concepire A' che si porta in A'' = T', laddove T' si è nel frattempo spostato in T'', e così via, all'infinito, sicché le successive posizioni di "Achille" sono i punti A, A' = T, A'' = T',... e i relativi percorsi sono i segmenti , ,.... , mentre quelle della tartaruga sono T, T', T'',... e i relativi percorsi , ,... . In tale suddivisione, di fatto, il punto A precede il punto T, il punto A' precede il punto T', etc., in eterno, per ogni coppia di punti corrispondenti nella successione. E' lecito per contro immaginare il duplice movimento (dell'inseguitore e dell'inseguito) in maniera diretta, "continua": A, che procede per esempio a velocità doppia rispetto a T, lo raggiunge dopo 2 secondi, indi lo supera definitivamente. Il punto chiave dell'aspetto sorprendente della situazione, nel resoconto che ne dà Simplicio, consiste in quel: <<non sarà mai raggiunto>>. Mai, cioè al trascorrere infinito del tempo. E' il "movimento pensato", ossia il pensare al movimento, il fenomeno che presenta aspetti paradossali, non il movimento reale, che semplicemente, come dicevamo, è oggetto della nostra esperienza ordinaria. Anzi, se esso, il movimento reale, non fosse, ecco che non potrebbe esserci alcun paradosso!

4. La più diffusa "soluzione" dei paradossi

Deve essere quindi secondo noi respinto il trasferimento sul piano "reale" degli argomenti di Zenone, e allo stesso modo va respinta la pretesa che si tratti di paradossi di natura linguistica, in altra parola di sofismi, artifici meramente dialettici, che traggono la loro origine dall'intrinseca "indeterminazione" del linguaggio¹⁶. Prima di addentrarci nell'analisi personale del problema, vogliamo accennare a quella che è la "soluzione" oggi più diffusa, almeno nell'ambiente dei fisici e matematici di professione (una "categoria" ovviamente inesistente fino a un paio di secoli fa), e forse anche dei filosofi (sempre intendendo fare affermazioni "di media"). Una soluzione che non ha nessuno dei predetti due torti (ossia: non esce dall'ambito ideale, e non considera la questione un vano gioco di parole), e che si può sintetizzare in alcuni versi che l'autore ricorda (nella traduzione inglese) affissi su un muro del Dipartimento di Matematica dell'Università di Cambridge (U.K.), al tempo dei suoi studi lassù - tali pertanto, per l'autorevolezza dell'istituzione che così indirettamente li avallava, da attenuare per lunghi anni (con quel giammai dimenticato <<poor old Zeno>>) ogni sua ulteriore curiosità in proposito:
 
 

Ciò equivale ad affermare che ogni studente oggi familiare con un po' di analisi matematica, sarebbe in possesso di una banale soluzione dell'enigma, consistente nella consapevolezza che una serie, una somma infinita di numeri, può, nonostante appunto la sua infinità, convergere, rappresentare un numero finito. Tale è manifestamente il caso della serie 1++++..., la cui somma è il numero 2. Questa serie corrisponde precisamente al percorso dell'Achille, nell'ipotesi che la sua velocità sia semplicemente doppia di quella della tartaruga, e che la loro distanza iniziale sia il segmento assunto quale unità di misura, cioè l'uno. Perciò abbiamo affermato che paradosso della dicotomia e dell'Achille coincidono sostanzialmente. Nel primo si prende in esame una successione di segmenti via via ridotti di un mezzo a ritroso, sicché sembra che il movimento non possa neppure iniziare; nel secondo, il movimento inizia ma per così dire non ha termine, e un'identica successione di segmenti viene costruita a partire dal segmento doppio di quello iniziale (ma scambiando l'ordine tra gli estremi).

Nota. Val forse la pena di spendere qualche parola sulla sostanziale, ma appunto non totale, uguaglianza dei due paradossi di cui ci stiamo occupando. Per la verità, nella formulazione del secondo il "principio del punto medio" (o dell'infinita suddivisibilità) non viene utilizzato, ma risulta per così dire conseguenza necessaria del movimento. Per essere più precisi, mentre nella dicotomia l'esistenza del punto medio viene esplicitamente supposta in fase di impostazione del discorso, nell'Achille invece, continuando a fare l'ipotesi che il rapporto tra le velocità sia di 2 a 1, quando l'eroe (che parte dal punto A) si trova dove era inizialmente la tartaruga (punto B), l'animale sarà situato nel punto medio M del segmento  contiguo al segmento , e ad esso uguale. Ciò implica l'esistenza di M a posteriori, e per questo abbiamo introdotto tale termine in modo alquanto criptico all'inizio del paragrafo 2: nell'Achille la dicotomia viene dedotta, non è premessa.

Respingiamo naturalmente anche la "soluzione infinitesimale", dal momento che il risultato matematico su cui si fonda non può non riconoscersi noto in sostanza pure all'intuizione primitiva di chiunque cominciasse a pensare a queste cose da un punto di vista "razionale", quali gli antichi Talete, Pitagora, Zenone, etc.¹⁸. Chi può davvero sostenere che essi non fossero in grado di comprendere esattamente, al pari di qualsiasi odierno studentello, la seguente ovvietà: se si aggiunge a un segmento la sua metà, e poi la metà di questa metà, e così via, non si supera mai il segmento doppio di quello inizialmente assegnato (e la relativa somma infinita, se si ritiene opportuno introdurre il concetto, deve ritenersi uguale a tale segmento doppio)?
 
 

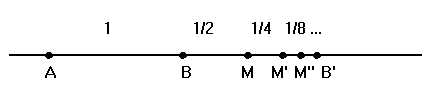
Nella figura si considerano un segmento  sulla retta ordinaria R, e un segmento "contiguo"  uguale ad . M è il punto medio di , M' il punto medio di , M'' il punto medio di , etc.. Se si assume  come unità di misura,  ha misura 1/2,  ha misura 1/4,  ha misura 1/8, e così via. E' evidente che, procedendo all'infinito, il segmento ++++... è proprio il segmento , doppio di , o, quanto meno, che ogni somma finita della serie in discorso è contenuta nel segmento , e quindi è sempre limitata. Ovvero, l'argomento non coinvolge mai la nozione di infinito "spaziale", come al contrario, per esempio, costringerebbe a fare l'introduzione di una semiretta, o dell'intera retta¹⁹.

Ci piace menzionare in tale frangente il nostro illustre professore di Storia delle Matematiche all'Università di Roma negli anni '60, Attilio Frajese, il quale contesta anch'egli chi rimprovera a Zenone di non essersi reso conto che una somma di infiniti segmenti o di infiniti intervalli di tempo può benissimo essere finita, purché queste grandezze vadano, con legge opportuna, indefinitamente diminuendo. Nel suo libro Attraverso la storia della matematica (Libr. Veschi, Roma, 1962) sostiene infatti apertamente che non sarebbe stato per nulla difficile, né per Zenone né per i matematici precedenti, giungere ai risultati più immediati relativi alla somma di serie (<<E' facile mostrare che anche agli albori della scienza matematica dovette essere assai semplice il calcolo della distanza in questione>>, p. 15). Secondo Frajese i paradossi non provengono da scarsa conoscenza (intuizione) della teoria delle serie, né intendono mettere in dubbio l'indubitabile (l'esistenza del movimento reale), bensì costituiscono una sorta di dimostrazioni per assurdo contro la presenza in geometria dell'atomismo (che si suol dire democriteo, ma Democrito è comunque più giovane di Zenone di alcuni decenni). Debbono essere interpretati cioè in chiave polemica con i Pitagorici, in contrasto con la "concezione monadica" degli enti geometrici da loro accolta. I paradossi di Zenone rientrerebbero quindi nella fase cosiddetta della "razionalizzazione della geometria", in cui si passò da una concezione della retta materialmente intesa²⁰ a una "ideale", con il conseguente necessario superamento del  ruolo del numero razionale (un semplice quoziente di interi) - caro appunto ai Pitagorici, che in esso scorgevano una manifestazione dell'armonia dell'universo - mediante l'introduzione di misure irrazionali. Si tratta di un punto di vista piuttosto autorevole, che procede dal famoso storico della matematica Paul Tannery, il primo, a quanto sappiamo, nella sua Pour l'histoire de la science hellène - De Thalès à Empédocle (1889), a formulare l'ipotesi che gli argomenti eleatici "contro il moto" fossero in realtà diretti principalmente contro il "punto esteso", ossia contro la descrizione atomistica della retta²¹.

Purtroppo all'origine di questo fraintendimento (una soluzione che non è affatto tale) sembra esserci proprio il filosofo alla cui memoria Episteme è dedicata. Fu infatti Cartesio (utilizzando un rapporto tra le due velocità di 10 a 1, e non di 2 a 1 come assumiamo qui) ad affermare che l'aporia dell'Achille:

<<non è difficile a risolversi, quando si consideri che alla decima parte di una quantità viene aggiunta la decima di questa decima, e cioè una centesima; e poi ancora la decima di quest'ultima, ossia una millesima della prima; e così di seguito all'infinito, tutte queste decime prese insieme, benché siano supposte realmente infinite, non compongono tuttavia che una quantità finita. Ché se taluno dice che una tartaruga, la quale ha dieci leghe di precedenza rispetto a un cavallo dieci volte più veloce di lei, non potrà mai essere superata da questo, perché mentre il cavallo compie le dieci leghe la tartaruga ne percorre una e, mentre il cavallo supera questa lega, la tartaruga procede ancora di un decimo di lega e così all'infinito, bisogna rispondere che veramente il cavallo non la sopravanzerà finché esso farà quella lega, quel decimo, quel centesimo, quel millesimo ecc. di lega; ma che non ne segue che non la supererà mai, perché quel decimo, centesimo, millesimo ecc. non fanno che un nono di lega, in capo al quale il cavallo comincerà a sopravanzarla>> (Lettres de M^r Descartes, Paris, 1657, N. 118; vedi pagina finale).

La citazione ha il merito di mostrare almeno che non c'è bisogno di arrivare all'analisi infinitesimale di Newton, Leibnitz e successori per avere un chiaro trattamento delle questioni preliminari relative a concetti quali limite, serie, convergenza, etc., che sono nelle possibilità di qualsiasi intelletto esordiente in tali elementari meditazioni. Il ragionamento di Cartesio avrebbe potuto benissimo essere formulato ai tempi di Zenone, e sarebbe rimasto inessenziale, mentre invece, alla luce del suo fondamentale dualismo, il grande pensatore francese avrebbe ben potuto intravedere il giusto scioglimento dell'enigma, dal momento che la res cogitans sta al tempo così come la res extensa sta allo spazio (cfr. pure il paragrafo 7)²².

5. Il dualismo spazio/tempo, oppure continuo/discreto

Esponiamo adesso la nostra "soluzione". Osserviamo prima di tutto che si deve riconoscere all'Achille zenoniano un merito: in effetti sembra davvero che A non possa raggiungere T, ed è questa circostanza che mette l'interlocutore <<di cattivo umore>>, come giustamente evidenziava Aristotele. Gli interrogativi da porsi allora sono: Perché avviene ciò? A quali caratteristiche degli enti coinvolti nel discorso si deve attribuire l'indubbio aspetto paradossale delle "dimostrazioni" di Zenone? Come mai ci troviamo quasi d'accordo con l'antico sapiente, nel negare la "possibilità razionale" del movimento?

Ecco la semplice risposta che proponiamo: l'intelletto umano non può concepire l'infinita suddivisibilità di un segmento temporale ("segmento" ci sembra termine più preciso che useremo d'ora in poi in luogo di "intervallo", sia per lo spazio che per il tempo, con lo svantaggio di dover però specificare il contesto, mentre comunemente "segmento" allude soltanto all'ambito spaziale, così come "intervallo" a quello temporale - a tale convenzione implicita avevamo anche noi fin qui aderito), con la conseguenza che una somma infinita di siffatti segmenti non può essere per esso altro che divergente. Un segmento temporale consiste invero di elementi indivisibili, che vengono denominati istanti, simili ai "punti" di un segmento spaziale, ma a differenza dei secondi, i primi appaiono costituiti solamente da un numero finito di istanti. Ciò costringe ad ammettere l'esistenza di un segmento "minimo", formato da due soli istanti, uno e il suo "successivo". Così, la somma di infiniti segmenti, che coinvolge necessiter infiniti istanti, non può essere mai un segmento²³. Dette constatazioni sono alla radice di quel mai nel brano di Simplicio!

Precisiamo il discorso (la comprensione di tutti i termini matematici che verranno utilizzati non è strettamente indispensabile, in prima lettura). Accanto alla retta spaziale R (o retta geometrica, o retta ordinaria, etc.), esiste - "nella nostra mente" - un'analoga retta temporale (espressione che potrebbe prestarsi a qualche equivoco, ma che ci pare comunque legittima), indichiamola con il simbolo T. Si tratta di un insieme ordinato, meglio spazio ordinato, che rappresenta il tempo nell'intelletto, allo stesso modo che R vi rappresenta lo spazio, almeno nella sua manifestazione 1-dimensionale. Le due "rette" si "assomigliano" di fatto sotto diversi aspetti, per esempio:

1 - sono entrambe costituite da infiniti "elementi indivisibili", chiamati rispettivamente "istanti" e "punti" (R viene descritta come collezione di punti "senza dimensione" sin dai primordi della geometria²⁴);

2 - possono essere (totalmente) ordinate (nell'enumerazione delle "differenze" tra R e T non andrebbe omessa però la circostanza che T appare dotato di una struttura d'ordine naturale, o canonica, mentre R no; se ne parlerà ancora nell'appendice), e nessuna delle due ha minimo o massimo;

3 - introdotto il concetto di segmento di estremi due assegnati istanti, o punti, distinti a e b, con a < b in un ordine fissato (come si accennava, in T c'è un ordine "canonico", in R bisogna sceglierne uno tra due, ma nella presente definizione la scelta è ininfluente), quale l'insieme di tutti quegli istanti, o punti, x tali che a £ x £ b (si tratta di un caso particolare del concetto generale di intervallo, di cui si discuterà in appendice; specifichiamo sin d'ora che si sta attualmente parlando di intervalli propri, attributo che si riferisce alla condizione a < b, e chiusi), è possibile operare un confronto tra segmenti, ossia riconoscere se un dato segmento è "minore o uguale" di un altro, dove "uguale" qui non ha nulla a che vedere ovviamente con l'eventuale identità tra i due segmenti in oggetto (una "relazione d'ordine" di un tipo però particolare, che si dice un preordine, si rimanda ancora l'appendice);

4 - rimane definita un'operazione algebrica (somma) non solo tra coppie di segmenti contigui (aventi cioè un estremo a comune), che è sempre lecita, ma anche tra coppie di "classi di equivalenza" di segmenti (l'equivalenza in questione è la precedente "uguaglianza");

5 - le due "strutture algebriche" che si ottengono sono molto "simili": semigruppi (l'operazione è associativa), ambedue privi di "elemento neutro" (lo zero proverrebbe dalla considerazione degli intervalli impropri, due di essi risulterebbero ovviamente equivalenti), abeliani (cioè commutativi), regolari (vale una naturale "regola di cancellazione", a+x = b+x implica a = b), ordinati, archimedei (cfr. il cap. VI delle dispense per le "strutture algebriche semplici", e http://www.dipmat.unipg.it/~bartocci/mat/cap10.doc per le strutture algebriche semplici ordinate);

6 - in dette strutture si può eseguire la misura di un segmento (di una classe d'equivalenza di segmenti) rispetto a un altro; etc..

La retta spaziale R è concepita però in maniera che tra un punto e l'altro ce ne sono sempre infiniti (anzi, come abbiamo visto nel paragrafo 2, tanti quanti quelli che esistono nell'intera retta), sicché non c'è alcun modo di introdurre il successivo di un determinato punto (in uno dei due ordini naturali che venga prescelto nell'ambiente). Al contrario, la retta temporale T appare formata da istanti "separati", ogni istante ha un successivo e un precedente, tra un istante e un altro non si riesce a immaginarne infiniti, e ne dà importante testimonianza il linguaggio comune, che sensatamente si serve dell'espressione "istante successivo", laddove nessuno mai parla, in un contesto spaziale, di "punto successivo". T è quello che si dice uno spazio ordinato discreto, mentre R è invece uno spazio ordinato continuo²⁵ (rimandiamo ancora una volta all'appendice): insomma, R e T non sono strutture isomorfe (per inciso, pure il fatto che lo "spazio" possa essere concepito in diverse "dimensioni", da 1 a 3, mentre il tempo viene immaginato in una sola dimensione, è secondo noi un ulteriore elemento significativo a favore della nostra tesi). E' lecito prendere in considerazione, sia in R che in T, delle serie, ossia delle somme infinite di segmenti, ed ecco che dalla fondamentale differenza strutturale tra le due "rette" procede la circostanza che deve ritenersi tanto l'origine dei paradossi, quanto la loro "soluzione": in R esistono delle serie di segmenti convergenti, in T ogni tale serie è necessariamente divergente.

Nota (investigazione delle leggi dell'intelletto). Il semigruppo delle classi di equivalenza di segmenti associato a R, indichiamolo con S , non ha né minimo né massimo, quello associato a T, diciamolo Q , non ha massimo, ma ha un minimo, la classe d'equivalenza dei segmenti con due soli istanti ("il" segmento con due soli istanti). Q può ritenersi coincidere proprio con N = { 1,2,3,...} , l'insieme dei numeri che si dicono naturali. E' forse opportuno sottolineare esplicitamente che, in virtù della nomenclatura proposta, la somma di due segmenti temporali, uno con m (³ 2) istanti, e l'altro con n, contiene m+n-1 istanti, poiché, in analogia con il caso spaziale, quando i due segmenti si considerano contigui onde poter introdurre il risultato dell'operazione, essi non sono disgiunti, bensì hanno un vertice in comune. Allo stesso modo, la misura di un segmento formato da k istanti rispetto al segmento minimo, che ne ha 2, è k-1, e non k (tale misura potrebbe dirsi "assoluta"). Ciò nonostante, vale l'attesa naturale proprietà additiva della misura (assoluta o no): la misura assoluta di un segmento con m istanti è m-1, di uno con n istanti è n-1, e la misura assoluta della somma è proprio (m+n-1)-1 = m+n-2 = (m-1)+(n-1), come desiderato (si può descrivere naturalmente la medesima fenomenologia in modo differente, ma noi abbiamo cercato di mantenere il più possibile l'analogia tra operazioni spaziali e operazioni temporali). La teoria della misura applicata ad R conduce all'insieme dei numeri reali positivi, simbolo R⁺; applicata a T, all'insieme dei numeri razionali positivi, simbolo Q⁺. Nella seguente figura abbiamo cercato di illustrare in modo elementare i fenomeni in esame, relativi alle proprietà di una "retta discreta", senza minimo e senza massimo.
 
 

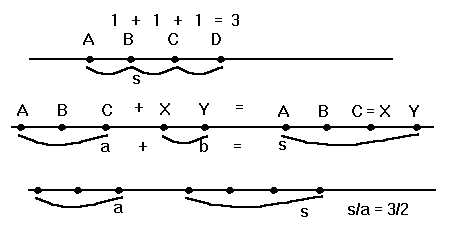
Nella prima riga si vede la misura assoluta di un segmento temporale costituito da 4 istanti, che è 3. Nella seconda, il risultato dell'operazione di somma tra un segmento a e un segmento b, risultato s (si intendono sempre classi d'equivalenza di segmenti). Nella terza, un esempio di misura non assoluta: la misura di s rispetto ad a è il numero razionale 3/2 (a si può dividere in due, s no).

Nota*. Si può comprendere più a fondo la differenza tra teoria della misura sulla retta continua R e sulla retta discreta T, notando che, introdotte le due funzioni misura m _R : S ´ S ® R⁺, m _T : Q ´ Q ® Q⁺, la prima si può "invertire" dando luogo a un'applicazione R^{+´ S} ® S (da cui poi si trae il famoso "prodotto esterno" di un numero reale per un vettore, una volta che venga trattata in maniera adeguata la questione dei segni, ossia l'introduzione di numeri reali negativi), la seconda no. Il perché è presto spiegato. Per la misura m _R vale un teorema del tipo: "comunque preso il numero reale positivo x, e un segmento a, esiste uno ed un solo segmento b tale che a/b = x, oppure b/a = x", mentre per la misura m _T tale asserzione non può ovviamente proporsi. E' istruttivo che la dimostrazione di questo teorema esclusivamente geometrico utilizzi o un'immersione di R nel piano ordinario P e la "teoria delle parallele" (teorema di parallelismo di Talete), oppure la proprietà di R di essere un continuo di II specie (vedi appendice), e che entrambe le possibilità sono precluse alla retta temporale T!

Forti delle precedenti considerazioni, torniamo all'analisi dell'Achille. Assieme alla serie spaziale +++... che l'argomento di Zenone introduce in modo esplicito (e che è scontato sia convergente, oggi come ieri: la sua "somma" è senz'altro il segmento doppio di , se continuiamo a supporre che la velocità di A sia doppia rispetto a quella di T), l'intelletto dell'ascoltatore è costretto a prendere in considerazione (almeno in un primo momento) anche la collegata serie dei relativi tempi di percorrenza. Indicando ancora con t il tempo impiegato da A per percorrere il primo tratto , o più precisamente il segmento di tempo compreso tra l'istante in cui inizia la corsa e l'istante in cui A si trova in T, ecco che  (e già questo è un concetto dal dubbio significato) dovrebbe essere il tempo impiegato da A per percorrere il secondo tratto , etc., sicché la serie temporale in oggetto sarebbe t +++... . Ma questa appare, come abbiamo detto, divergente, per la natura intrinseca dei suoi addendi, che sono segmenti temporali, mentre la situazione costringerebbe contemporaneamente a ritenerla limitata (contenuta cioè in un determinato segmento, attualmente il doppio di t ), e pertanto convergente. Il matematico che volesse prescindere infatti dalla natura degli elementi della serie, la scriverebbe immediatamente nella forma t (1+++...), e direbbe che il risultato è banalmente 2t , tra l'altro non facendo sufficiente attenzione alla differenza tra il "tempo" t e la "misura" di esso. Ma non si possono introdurre tempi, né a maggior ragione una loro misura, che non esistono, i.e. che non possono essere concepiti, come accade al tempo  (e non c'entra tanto il crescere dell'esponente n: già  potrebbe non avere senso). Insomma, l'assurdo è che la serie t +++... va considerata divergente e convergente, la soluzione è che detta serie non può neppure pensarsi, dal momento che non sono pensabili tutti i suoi successivi termini. [Tralasciamo la questione del numero "pari" o "dispari" degli istanti contenuti in un segmento, che pure avrebbe diritto di cittadinanza, istruendo, sotto l'aspetto empirico, sulla diversità tra una misura "esatta" e una "approssimata", e, sotto quello ideale, sulla circostanza che, secondo l'impostazione da noi proposta, non è sempre possibile introdurre nemmeno la metà di un segmento temporale - come si dice, il semigruppo delle classi di equivalenza di segmenti temporali non è divisibile, ossia, assegnato un numero naturale n, l'equazione nx = a, nell'incognita x, e fissato il segmento a, non è sempre risolubile. Ad esempio, quando n = 2, l'equazione precedente ha soluzione se e soltanto se a è composto da un numero dispari di istanti.] L'accennata impossibilità è la stessa, mutatis mutandis, che ci impedisce di costruire "immagini mentali" di spazi di dimensione superiore a tre²⁶, o geometrie non euclidee, etc.. Tutti enti ben "razionali", almeno in un certo senso²⁷, si intende, e in quanto tali matematicamente trattabili, ma, ribadiamo, non "oggetti di intuizione". Ciò dipende dal modo con cui l'intelletto è costituito, un "dato di fatto" che non può essere ignorato. Si crede di poter perfettamente comprendere la serie t +++... come una serie temporale, ma in realtà si concepisce soltanto la corrispondente serie spaziale (ossia, la serie dei relativi percorsi), o, se si preferisce, la serie numerica delle relative misure (quando si sostituisca a t il valore 1, come è peraltro sempre lecito se si assume t come "unità di misura" del tempo). I termini delle due ultime serie specificate hanno perfetto significato nei loro ambiti di competenza, ma non ne hanno, non ne possono avere, in veste di candidati a descrivere enti che si rifanno alla concezione comune del tempo.
Potremmo anche osservare che la somma della serie infinita numerica 1+++... viene concepita in un tempo finito, ma che non altrettanto accade per la successione di tutte le sue somme parziali: 1, 1+, 1++,..., la quale richiede almeno un istante di tempo per la comprensione di un singolo termine della successione, e quindi nel complesso quello che sarebbe un tempo infinito. Perciò i matematici scrivono il "termine generale"  [o la somma parziale generale, vale a dire 1++..+ =  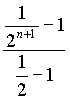= 2* (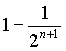) = 2-] di una serie come questa, introducendo un "parametro" n, e costruendo così un'espressione che è una: concepibile in un tempo finito, archetipo di tutte le infinite sue "specializzazioni" al variare di n, che non importa comprendere "una a una".

In altre parole ancora, appare impossibile stabilire, per le caratteristiche proprie degli enti coinvolti, una corrispondenza biunivoca tra segmenti di spazio ideale percorso (elaborazioni della pura geometria della retta continua ideale), e associati segmenti di tempo. Ovvero, la nostra mente è costretta a concepire delle posizioni spaziali virtuali che non possono essere effettive, non possono essere di fatto occupate, non esistendo un istante in cui tale "occupazione" possa avere luogo. Una coppia ordinata del tipo posizione-istante, o spazio-tempo, è quello che si dice un evento, e potremo allora pure sintetizzare la nostra opinione asserendo che: non ogni posizione spaziale del tragitto di Achille corrisponde a un evento.

Nota. Si badi bene che ciò non accade perché i punti della retta sono irrimediabilmente "di più" (nel preciso senso dato da Cantor a tale espressione anche per gli insiemi infiniti; cfr. per esempio http://www.dipmat.unipg.it/~bartocci/mat/cap5-2.doc) degli istanti temporali, che sono invece, secondo la nostra convinzione, concepibili esclusivamente come un'infinità numerabile. In effetti, nell'argomento di Zenone solo il numerabile ("discreto") è coinvolto, cioè una successione di segmenti spaziali, cui non può corrispondere un'analoga successione di segmenti temporali. Il fatto è, ripetiamo ancora una volta, che un segmento spaziale si può suddividere in un'infinità di sue parti, ancora segmenti, per esempio effettuando successive dicotomie, mentre ciò non appare altrettanto "intuitivamente" possibile per i segmenti temporali. Rimane in ogni caso la circostanza che la retta temporale è, in quanto insieme, cantorianamente più piccola della retta spaziale (o di un segmento spaziale, che è uguale all'intera retta). Vale a dire, R e T sono strutture non isomorfe, né se le si riguarda come spazi ordinati, né come insiemi. Ritorneremo su tali osservazioni nell'ultimo paragrafo dell'appendice, in sede di "riassunto" in termini strettamente matematici del dualismo da noi ritenuto "soluzione" dei paradossi.

Nella spiacevole "contraddizione" in cui l'intelletto umano si trova a precipitare quando riflette sul discorso di Zenone, ossia nel conflitto tra un modello continuo (spaziale) e uno discreto (temporale) - entrambi indispensabili alla nostra mente per concepire il movimento, che è appunto variazione dello spazio nel tempo - consiste, ribadiamo, l'innegabile connotato paradossale che da secoli affascina i "filosofi" (intesi nel senso più ampio del termine). Una sola serie, e non due; una serie convergente all'interno di un contesto continuo, laddove invece serie all'interno di un contesto discreto sono esclusivamente divergenti; un avverbio, quel "mai", di tempo e non di luogo; una simultanea contemplazione di due strutture irrimediabilmente contrapposte, ecco l'essenza dei paradossi di Zenone, che ci rende di cattivo umore, facendo "oscillare" indeterminatamente la risposta tra: sì la raggiunge / no, non la raggiunge (a seconda che prevalga l'aspetto spaziale, o quello temporale). Il perenne lato istruttivo di essi, all'origine del costante interesse che li circonda, risiede nella circostanza che ci costringono a prendere atto di questo dualismo, una semplice constatazione che non riesce a persuadere chi è ormai abituato a confondere lo spazio con il tempo, mediante una loro pretesa comune "misura", e quindi attraverso l'unico concetto di "numero reale", che esprime in effetti le sole misure geometriche di segmenti. Introducendo tali numeri²⁸ si crede di riuscire a definire qualcosa relativa al tempo, ma si lavora in realtà unicamente con lo spazio. Si scambia cioè la necessaria (per l'intuizione umana dello spazio) infinita suddivisibilità dei segmenti della retta spaziale R, con una corrispondente infinita suddivisibilità degli analoghi segmenti della retta temporale T, invece impossibile per l'intuizione umana.

Discutiamo degli esempi. Un amante prega l'amato che lo sta lasciando: rimani ancora un secondo con me, mezzo secondo, un quarto di secondo, etc., e ciascuno capisce che gli sta domandando invero di restare per l'eternità, e non per soli due secondi. Analogamente, non ha alcun significato (né "pratico", e fin qui si sarebbe forse tutti d'accordo, ma neppure "concettuale") dire, al momento di fissare un appuntamento: vediamoci tra p secondi, o ore, o qualsiasi altra unità di misura del tempo si desideri. Lo stesso varrebbe ovviamente per  secondi, e su ciò converrebbero probabilmente molti, ma bisogna riconoscere inoltre che non ha neanche senso dire, almeno a priori, vediamoci tra 7/12 di secondo. Mentre infatti non c'è difficoltà a interpretare il numero razionale 7/12 in un contesto spaziale (è sempre lecito costruire i 7/12 di un segmento di R), i 7/12 di un segmento temporale arbitrariamente fissato potrebbero invece "non esistere" (si rammenti la seconda nota di questo paragrafo), sicché il riferimento a un tale periodo di tempo potrebbe essere inteso soltanto come 7 "clic", posto 1 clic uguale a 1/12 di secondo (e presupponendo di possedere quindi uno strumento di misura del tempo, un orologio, che misuri i clic - essi sono per noi segmenti temporali, si badi bene, e non singoli istanti)²⁹. Ancora, ammesso un fiat di pensiero (di "coscienza") per ogni segmento temporale, se uno di questi fosse infinitamente suddivisibile, ecco che di conseguenza sarebbero possibili infiniti atti del pensiero, infinite decisioni, in un tempo finito, circostanza che appare assurda alla nostra percezione del tempo, anche perché esso è inesorabile edax rerum: scorre e tracima con sé tutte le cose, sicché non è lecito "scherzarci sopra"³⁰.

Concludiamo il paragrafo sottolineando che la filosofia di Kant (seppure ormai da cent'anni sia invalsa la moda di denigrarla³¹, facendo del suo autore quasi il drago Aristotele contro cui dovette combattere l'eroe Galileo) si propone quale la più conforme a risolvere l'indiscutibile e perenne perplessità che suscita, deve suscitare, generazione dopo generazione, l'argomento zenoniano, e ricordando come tale filosofia viene sintetizzata da Hegel, proprio in relazione al problema qui trattato:

<<Questa è dunque la dialettica di Zenone: egli ebbe coscienza delle determinazioni contenute nelle nostre rappresentazioni di spazio e di tempo, e ne ha dimostrato le contraddizioni. Le antinomie di Kant non vanno oltre quanto aveva già veduto Zenone. Il risultato generale della dialettica eleatica è stato quindi il seguente: "il vero è soltanto l'uno, tutto l'altro non è vero"; allo stesso modo che il risultato della filosofia kantiana è questo: "noi conosciamo soltanto fenomeni". In complesso si tratta dello stesso principio: "il contenuto della coscienza è soltanto fenomeno, non verità"; tuttavia vi è anche una grande differenza. Infatti Zenone e gli Eleati dettero alla loro teoria questo significato: "il mondo sensibile, con le sue formazioni infinitamente varie, in se stesso è soltanto apparenza e non ha verità". Invece Kant è di opinione diversa ed afferma: "siamo noi che, applicando l'attività del nostro pensiero al mondo esteriore, lo rendiamo fenomeno; e l'esteriore diventa non vero soltanto perché noi gli applichiamo una quantità di determinazioni. Pertanto solo la nostra conoscenza, vale a dire il lato spirituale, è fenomeno, mentre il mondo in sé è assolutamente vero; il nostro procedere lo rovina, e l'opera nostra non approda a nulla">> (Lezioni di storia della filosofia)³².

6. Alcune prevedibili obiezioni

Non si ritenga quella precedente una conclusione scontata, largamente condivisa, anzi. Secondo Federigo Enriques, per esempio, sulla scia del citato Tannery, i paradossi hanno addirittura una natura solo geometrico-spaziale, senza coinvolgere il tempo: <<Il valore dei primi due argomenti ci appare indipendente da ogni considerazione di tempo>>³³. Tanto per accennare a un caso significativo che pur prende in doverosa considerazione l'aspetto temporale, H. Weyl afferma esattamente il contrario di ciò che asseriamo: <<Esempi particolarmente importanti di sistemi continui sono lo spazio e il tempo>> (loc. cit. nella nota 30, p. 46). Sulla medesima posizione si trova anche Bernhard Bolzano: <<Si deve, certo, convenire che due istanti qualsiasi sono separati da un insieme infinito di istanti tra essi compresi>>³⁴. Insomma, essendo la continuità di I specie - come proporremo di chiamarla precisamente nell'appendice - una caratteristica indiscussa dello spazio (delle sue rette), ecco che lo spazio e il tempo vengono a essere concepiti allo stesso modo, e proprio per merito, potrebbe sembrare, di ... Zenone! Una tentazione apparentemente irresistibile è infatti quella di ascrivere al tempo tutte le caratteristiche possedute dallo spazio, quale unica via di uscita dai paradossi: sarebbero questi ad additare la necessità di una "corrispondenza biunivoca" (isomorfismo) tra la retta spaziale R e la retta temporale T. Così illustra la situazione il nominato T. Viola:

<<riteniamo tutti e quattro i paradossi come una critica sia dello spazio che del tempo. Riteniamo poi che, nell'intenzione di Zenone, essi debbano avere un significato unitario e precisamente [...]: 1) siano rivolti essenzialmente ai pitagorici; 2) non riguardino la cosiddetta crisi degl'irrazionali; 3) accettino (ritenendola già acquisita) la concezione geometrica contraria al "paleo-pitagorismo" (o pitagorismo arcaico), ammettano cioè la concezione della densità di distribuzione dei punti di un segmento, proponendosi di convincere i pitagorici, con intento polemico, ad accettare l'analoga concezione della "densità di distribuzione" degl'istanti di un intervallo di tempo>> (enfasi nel testo)³⁵.

Senz'altro ben spiegato, né si può escludere che proprio questa fosse l'intenzione originale di Zenone, ma, ripetiamo, esattamente agli antipodi di quella che qui difendiamo come corretta: una volta di più, invece di prendere atto reverente di una differenza (che in quanto esistente è pure probabilmente istruttiva), si preferisce ridurre il due all'uno.

Dedichiamo qualche cenno alle principali critiche - peraltro ben note - che al nostro approccio alla questione zenoniana possono venire mosse, in conformità con lo Zeitgeist in precedenza sommariamente delineato. Una prima si può riassumere nel seguente interrogativo: chi può assicurarci che l'intuizione dello spazio e del tempo siano davvero quelle qui descritte, e che oltre tutto siano identiche per ogni essere umano? La seconda, di origine schiettamente darwinista, aggiungerebbe: pur ammesso che quelle proposte siano descrizioni adeguate, e universali in un certo momento dello sviluppo dell'uomo, chi assicura che siano sempre state tali, o che lo saranno ancora in futuro?

La prima (di sapore scettico-relativistico) non ha risposta se non attraverso un'approfondita analisi delle modalità con cui si esplica la nostra personale "intuizione" (la parola allude in realtà più all'atto del "guardare dentro", che non all'oggetto che si indaga, vedi la nota 42). Ciascun risultato del procedimento di intuizione lo si può determinare da se stessi, senza alcun bisogno dell'autorità di altri, o della loro testimonianza, a differenza delle verità di natura storica, o sperimentale, anche se il lavoro già effettuato, e registrato, può agevolare lo studio dei fenomeni osservati, o evitare errori. Si estendono poi legittimamente le conclusioni raggiunte a ogni essere umano in conformità a una sorta di principio di universalità (non a caso Cartesio introduce il cogito nella forma di prima persona singolare, e non plurale). Ammetteremmo più facilmente che la descrizione da noi proposta è sbagliata (non conforme cioè alle reali caratteristiche delle intuizioni esaminate), piuttosto che ne possano esistere tante diverse. La disparità delle opinioni in situazioni come la presente (che riguardano questioni "fondamentali") può essere ricondotta a molteplici fattori. Per esempio a insuperabili condizionamenti esterni (<<tutte queste verità possono essere chiaramente percepite, ma non da tutti, a causa dei pregiudizi>>, Cartesio, Principia Philosophiae, Parte I, 50), o a mancanza di sincerità assoluta nell'esposizione della propria opinione (un fenomeno più diffuso di quanto si potrebbe immaginare su due piedi, e a cui accenna T. Paine nel brano riportato nel presente numero di Episteme - un commento dalla redazione di Episteme al libro di G. Sebasti, subito dopo la nota 4). Né andrebbe sottovalutata l'inclinazione a scambiare ipotesi con certezze (spesso al di là delle intenzioni dei loro primi formulatori, ma talora per difetti di "traduzione", i famosi fraintendimenti linguistici anche all'interno della medesima lingua, talora per l'abitudine a ripetere acriticamente il pensiero di altri, con l'effetto di provocare gradualmente delle involontarie trasformazioni semantiche degli enunciati originali); a voler modificare eventuali verità spiacevoli dal punto di vista di qualche "ideologia", sostituendole allora con i propri desideri (ciò che si vorrebbe fosse, in luogo di ciò che risulta: una tendenza aggravata dalla scarsa disponibilità ad ammettere che quest'ultimo possa essere assai poco); a semplificare indebitamente perché ci si "stanca" presto (<<il nostro spirito si stanca, quando presta attenzione a tutte le cose di cui giudichiamo>>, Cartesio, Principia Philosophiae, Parte I, 73); etc.. Insomma, un ampio prontuario di umane debolezze, che rendono a volte difficile un consenso (meditato, e non imposto, soprattutto frettolosamente, come spesso invece intorno a noi si esige) perfino sulle asserzioni più elementari (il consenso potrebbe del resto verificarsi pure su un dubbio, o su un'alternativa).

Alla seconda obiezione si può rispondere che nessuno sa veramente come stiano le cose in tale contesto, e valutare la maggiore o minore probabilità del mutare dell'intuizione. Ciò può essere effettuato solo all'interno di concezioni teorico-sperimentali che appaiono tanto più incerte nella misura in cui sono più ampie. Certo è che l'intuizione umana del tempo e dello spazio sembra immutata da millenni a questa parte, anzi da tutte le notizie che abbiamo a disposizione sui nostri predecessori (checché se ne dica). Se si leggono Platone, o Proclo, che scrive circa ottocento anni più tardi, e poi altri secoli dopo Cartesio, o lo stesso Einstein, si ha l'impressione di essere sempre davanti al medesimo intelletto, diverso semmai per quantità di informazione, e di elaborazione, ma non per qualità di comprensione, di intuizione, e di "logica" (Einstein, per giustificare la necessità di modificare in fisica le concezioni ordinarie dello spazio e del tempo, onde poter conciliare "principi" apparentemente inconciliabili, usa proprio tali concezioni ordinarie, il contrario sarebbe stato impossibile). Riteniamo opportuno rammentare qui le parole di Pietro Martinetti che sono state prescelte quale motto per Episteme N. 6, parte I, il cui "succo" è: ammessa pure come "fenomeno" la relatività di certe opinioni, essa riposa sulla relatività della conoscenza umana degli argomenti che sono l'oggetto di queste opinioni , non su d'una relatività storica degli oggetti in questione. Al contrario H. Weyl afferma che: <<l'intuizione non è uno stato felice e ininterrotto: essa viene spinta innanzi verso la dialettica e l'avventura della conoscenza>> (loc. cit. nella nota 30, p. 31), secondo noi però contraddicendosi subito dopo: <<Sarebbe follia attendersi che la conoscenza riveli all'intuizione qualche segreta essenza delle cose nascosta dietro ciò che è dato manifestamente per intuizione>> (p. 32). Come dire che se si possono fare (e si sono fatti) grandi passi in avanti nell'analisi dei concetti, e nel campo dei giudizi sintetici a posteriori (esperienza fisica), c'è meno da attendersi nell'ambito dei giudizi sintetici a priori³⁶. Pensiamo che siano pertinenti al riguardo anche le seguenti considerazioni di Blaise Pascal (spesso eccessivamente "sentimentale", qui l'intuizione diventa "le coeur", ma molto sensato):

<<Nous connaissons la vérité non seulement par la raison mais encore par le coeur. C'est de cette dernière sorte que nous connaissons les premiers principes et c'est en vain que le raisonnement, qui n'y a point de part, essaie de les combattre. Les pyrrhoniens, qui n'ont que cela pour objet, y travaillent inutilement. Nous savons que nous ne rêvons point. Quelque impuissance où nous soyons de le prouver par raison, cette impuissance ne conclut autre chose que la faiblesse de notre raison, mais non pas l'incertitude de toutes nos connaissances, comme ils le prétendent. Car l(es) connaissances des premiers principes: espace, temps, mouvement, nombres, sont aussi fermes qu'aucune de celles que nos raisonnements nous donnent et c'est sur ces connaissances de coeur et de l'instinct qu'il faut que la raison s'appuie et qu'elle y fonde son discours. Le coeur sent qu'il y a trois dimensions dans l'espace et que les nombres sont infinis et la raison démontre ensuite qu'il n'y a point deux nombres carrés dont l'un soit double de l'autre. Les principes se sentent, les propositions se concluent et le tout avec certitude quoique par différentes voies - et il est aussi inutile et aussi ridicule que la raison demande au coeur des preuves de ses premiers principes pour vouloir y consentir, qu'il serait ridicule que le coeur demandât à la raison un sentiment de toutes les propositions qu'elle démontre pour vouloir les recevoir. Cette impuissance ne doit donc servir qu'à humilier la raison - qui voudrait juger de tout - mais non pas à combattre notre certitude. Comme s'il n'y avait que la raison capable de nous instruire, plût à Dieu que nous n'en eussions au contraire jamais besoin et que nous connussions toutes choses par instinct et par sentiment, mais la nature nous a refusé ce bien; elle ne nous a donné au contraire que très peu de connaissances de cette sorte; toutes les autres ne peuvent être acquises que par raisonnement>> (Pensées, 110).

Ancora in tema di "variabilità" dell'intuizione, per replicare a coloro, e sono purtroppo numerosi, che invocano a sproposito la scoperta delle "geometrie non euclidee" quale elemento capace di modificare l'umana percezione dello spazio (cfr. la nota 31), ci sembra utile riportare la replica del filosofo e sociologo Georg Simmel (1858-1918) - parole che sovente presentiamo all'attenzione dei nostri interlocutori, visto che nessun altro lo fa, auspicandone una sempre maggiore diffusione³⁷:

<<Gli assiomi geometrici sono così poco necessari logicamente come la legge causale; si possono pensare spazi, e quindi geometrie, in cui valgono tutt'altri assiomi che i nostri, come ha mostrato la geometria non euclidea nel secolo dopo Kant. Ma essi sono incondizionatamente necessari per la nostra esperienza, perché essi solamente la costituiscono. Helmholtz errò quindi completamente nel considerare la possibilità di rappresentarci senza contraddizione spazi nei quali non valgono gli assiomi euclidei come una confutazione del valore universale e necessario di questi, da Kant affermato. Infatti l'apriorità kantiana significa solo universalità e necessità per il mondo della nostra esperienza, una validità non logica, assoluta, ma ristretta alla cerchia del mondo sensibile. Le geometrie anti-euclidee varrebbero a confutare l'apriorità dei nostri assiomi solo quando qualcuno fosse riuscito a raccogliere le sue esperienze in uno spazio pseudo-sferico, o a riunire le sue sensazioni in una forma di spazio nel quale non valesse l'assioma delle parallele>>.

Di fronte al fenomeno dell'immutabilità di talune concezioni, malgrado tutti gli sforzi profusi perché avvenisse il contrario, Richard L. Faber sostiene per esempio che la colpa della mancata accettazione a livello comune delle concezioni einsteiniane dello spazio e del tempo (alle quali accenneremo nel paragrafo 8) sia imputabile alla circostanza che idee preconcette di spazio e di tempo sono state impiantate nelle nostre menti e rinforzate per tanti anni (<<You will be asked to abandon some of the preconceived ideas of space and time that have been implanted in all our minds and reinforced over many years>>, Differential Geometry and Relativity Theory, M. Dekker, 1983, p. 110). Nonostante tali lamentazioni (la colpa è tutta ... dei maestri d'asilo), la relatività continua a mantenere il suo carattere anti-intuitivo, a cent'anni dalla nascita, e i relativisti seguitano a rimanere in speranzosa attesa che si realizzi la profezia adombrata nelle parole di Faber: quando il condizionamento contrario sarà finalmente superato, i nostri figli riusciranno tranquillamente a concepire spazi a più dimensioni, eventualmente curvi, tempi inclusi nelle dimensioni spaziali, o a "riunire le loro sensazioni in spazi nei quali non vale l'assioma delle parallele".

In effetti, invece, nulla è veramente cambiato sotto il profilo in oggetto, a mostrare l'inefficacia di certe "rivoluzioni", e degli affrettati proclami di vittoria di competenti incompetenti apologeti. La condizione dell'insegnamento universitario della matematica e della fisica è tale e quale la denunciò H. Weyl parecchi anni fa, in esso permanendo una <<rozza e superficiale mistura di sensismo e di formalismo che [...] gode ancora di grande prestigio tra i matematici>>³⁸. Parole con cui l'ultimo dei grandi geometri di Göttingen intendeva probabilmente suggerire che venisse eliminata la componente "sensista" in favore della "formalista", la scelta del termine esprimendo implicitamente una forma di "disprezzo" per una soluzione al problema dei fondamenti ritenuta meno "nobile". Del resto, gli stessi intenti sembrano avere coloro che liquidano ogni approccio simile a quello da noi illustrato tacciandolo di "psicologismo", né potremmo usare il più adeguato "intuizionismo", perché di esso si sono impadroniti alcuni eccentrici "finitisti", che hanno dato dell'intuizione un'interpretazione così restrittiva-riduttiva da stentare naturalmente ad avere seguito³⁹. Insomma, non è stato lasciato nemmeno un vocabolo appropriato per definire senza fraintendimenti posizioni quali la nostra⁴⁰! [Come dice bene il filosofo Rocco Ronchi (vedi questo stesso numero di Episteme, sezione Reprints, articolo N. 1): <<il massimo potere sta nella parola. Chi parla per primo controlla l'universo>>.]

Concludiamo affermando che la lotta all'intuizione, lo sforzo di eliminare, o diminuire, il suo indispensabile ruolo nei "fondamenti" di ogni disciplina, non è stata una conseguenza inevitabile di un oggettivo progresso della conoscenza scientifica fattuale, bensì un atteggiamento filosofico a priori (una moda), che viceversa ha guidato l'interpretazione di quel "progresso" in ambienti ristretti. Questi hanno poi esercitato, venendosi a trovare in posizione di predominio per alterne vicende, influenza sproporzionata su tutti gli altri, che dopo un po' hanno finito con il seguire passivamente i nuovi mastri pifferai (indiscutibilmente molto bravi da un punto di vista tecnico) anche nelle loro "stravaganze"⁴¹.

7. Un altro più essenziale rimosso dualismo, quello tra materia e spirito

Abbiamo già accennato nella nota 12 all'imperfetta corrispondenza del dualismo reale/pensato con res extensa/res cogitans. La "soluzione" proposta nel paragrafo 5 si rifà a un dualismo presente strettamente nel pensato, ovvero nell'intelletto (un ulteriore sinonimo è per noi "ragione"), che non è esattamente la componente "spirituale" dell'uomo (la moderna terminologia informatica permetterebbe di pensare al cervello come a un hardware dotato di un ben preciso sistema operativo, un software, ad alcuni modi di funzionamento del quale ci si può genericamente riferire con le espressioni "spazio" e "tempo"). Per quest'ultima non troviamo (in parole) definizione migliore di quella che si deduce da taluni passi della Summa Theologiae di S. Tommaso, dove si introduce il termine voluntas: è la voluntas che utilizza lo "strumento" intelletto, con cui sceglie, decide⁴². [Esistono, nel deposito di ciò che ci è stato tramandato dai nostri padri, degli spunti, delle riflessioni, delle parole chiave, che fanno mettere le ali per volare in cielo, ed altri che fanno sprofondare agli inferi: alla nostra voluntas sta appunto di "scegliere" quali.] Essa ha chiaramente a che fare anche con la questione del libero arbitrio, e quindi con il dualismo tra determinato (caratteristico dell'ambito spirituale) e indeterminato (proprio invece dell'ambito materiale).

Tale impostazione permette di comprendere il senso di descrizioni della scientia, o della veritas, quali adaequatio, sia che si tratti di adaequatio intellectus et rei, secondo la nota definizione tomistica, o di adaequatio rei ad intellectum, secondo la definizione che ne dà invece Nicola Cusano⁴³. Consente anche, per esempio, e la cosa ci interessa particolarmente, di affrontare il problema della "verità" degli assiomi di una teoria matematica "fondamentale": non c'è infatti "assioma" che da una proprietà delle strutture di base non derivi. [Con il termine "fondamentale" vogliamo introdurre un'opportuna distinzione tra le teorie che sono alla base della riflessione matematica - sostanzialmente soltanto aritmetica, "numeri naturali" e "numeri razionali", riconducibile al "tempo", e geometria, "numeri reali", riconducibile allo "spazio" - e le relative "generalizzazioni" (vedi la nota 1 dell'appendice), talora ispirate pure da motivazioni esclusivamente ludiche.] Gli assiomi non sono semplici "convenzioni", più o meno "utili", come riteneva Henri Poincaré, né è la sola compatibilità logica interna quella che conta, come proponeva David Hilbert. Essi vanno invece "giudicati" in ordine alla loro adeguatezza a descrivere oggetti "noti" del pensiero (vedi anche la nota 14). La decisione se un determinato enunciato abbia o non abbia la richiesta qualità è di competenza esclusiva della voluntas⁴⁴.

Può riconoscersi allora senza eccessiva difficoltà che il tempo corrisponde in qualche modo allo spirito ("flusso" dell'umana coscienza), così come lo spazio alla materia - o meglio, a spirito e materia anch'essi in quanto "pensati", oggetti cioè di riflessione da parte dell'intelletto. Il tempo esprime una condizione necessaria per avere consapevolezza (pensare) della propria esistenza (in quel "presente continuo" del cogito cartesiano è implicita la durata dell'atto), fosse pure per un "quanto di tempo". Per contro, lo spazio appare una condizione necessaria della materia, della possibilità di concepire qualsiasi oggetto, o corpo, "materiale" (vedi il paragrafo 9). Confrontando la descrizione precedente con quella data da Cartesio, concordiamo con lui nel ritenere che l'estensione sia invero attributo indispensabile della materia, mentre ci sembra che sia piuttosto il tempo, e non il pensiero, l'analogo attributo fondamentale dello spirito (<<ogni sostanza ha un attributo principale, [...] quello dell'anima è il pensiero, come l'estensione è quello del corpo>>, Principia Philosophiae, Parte I, 53). Ciò sommariamente premesso, non è assurdo congetturare che l'opposizione al dualismo spazio-tempo potrebbe avere quale autentico obiettivo l'altro più profondo dualismo tra materia e spirito. E' siffatto dualismo che certo pensiero riduzionista moderno vuole davvero combattere, negando l'esistenza dello spirito (e della "vita") in quanto forma primitiva a sé stante del "manifestato". Non sarebbe difficile trovare numerosi esempi a illustrazione di questa interpretazione, ma ragioni di spazio (e di tempo) ci costringono a sorvolare. [Solo un cenno alla questione che tale riduzionismo può ben definirsi genericamente materialistico, anche se qui riduce lo spazio al tempo (secondo noi contrapposto alla "materia"), eliminando dai "fondamenti" la geometria in favore dell'aritmetica. La scelta non è dovuta ovviamente a motivazioni "spirituali", bensì soltanto alla pretesa maggiore "semplicità" della seconda disciplina rispetto alla prima. Attrae cioè l'aspetto "meccanico" dell'iterazione, preludio alle macchine calcolatrici, e alle tesi della cosiddetta "intelligenza artificiale", un tema sul quale ci limitiamo a ricordare l'articolo di Rocco Vittorio Macrì in Episteme N. 4.]

8. I paradossi di Zenone e la teoria della relatività

Questo scritto non sarebbe completo se non si aggiungesse un ulteriore elemento in risposta alla prevedibile domanda: come mai una soluzione tanto semplice quale quella qui proposta è così poco comune? Perché non la si illustra senza accenni polemici ai "predecessori", ai "grandi" che l'opinione pubblica ha giustamente collocato nel moderno Olimpo della scienza?

In effetti, come abbiamo accennato nella nota 10, dopo il lungo oblio del medioevo (e talune tracce di un sopravvissuto interesse per Zenone presso gli Arabi: si veda Franz Rosenthal, "Arabische Nachrichten über Zenon den Eleaten", Orientalia, 6, 1937), la ripresa del dibattito in proposito avviene in Europa solo nel XVII secolo, e, subito dopo il menzionato Cartesio, spazio e tempo si trovano in qualche modo già "confusi" nella neonata "meccanica razionale" newtoniana, mediante l'identificazione dei due concetti attraverso la loro misura espressa tramite un numero reale. Si pensi infatti alla formula s = vt, spazio uguale velocità per tempo (anche qui largamente usata), che viene concepita come un'identità tra numeri reali, onde poter poi applicare ad essa gli algoritmi del calcolo infinitesimale (stiamo esaminando ovviamente il caso di un moto uniforme). Per v = 1, nel sistema di misura prescelto, essa implica s = t, spazio = tempo, un "vizio originale" del "modello"⁴⁵ continuo di Newton, rivelatosi comunque certamente "utile" (alcuni epistemologi "di sinistra" userebbero con compiacimento il termine "progressivo"), perché permetteva di fare certi calcoli, e formulare quindi certe "previsioni", in modo assai semplice, quasi automatico (che è il massimo che riescono ad apprendere - e che ci si limita a pretendere oggi, conformando di conseguenza l'insegnamento - molti studenti di matematica). Vale a dire che quel "vizio" non ne inficia la corrispondenza al reale (applicabilità), almeno fino a che non si spinga il modello ai propri limiti, come accade nelle odierne "teorie del caos" (oggi di gran moda per le loro evidenti, e ahimé attuali, allusioni sociologiche). Basterebbe soltanto di tali limiti essere "consapevoli".

Se è già intrinsecamente non conforme a realtà il modello continuo newtoniano dello spazio-tempo (se ne discuterà ulteriormente nel prossimo paragrafo), un modello continuo assai peggiore sotto il punto di vista che ci sta a cuore è quello di Einstein-Minkowski, dove spazio e tempo sono per così dire ancora più confusi: addirittura relativi all'osservatore, fatto che dà inizio a tutta una serie di nuovi paradossi (molto popolare quello "dei gemelli", vedi quanto se ne dice nel punto 4 di http://www.dipmat.unipg.it/~bartocci/listafis.htm). Ciò avviene in conformità al "manifesto" che l'<<architetto formalista>> della relatività "ristretta" (aggettivo che distingue da una successiva relatività "generale", consistente in una teoria relativistica della gravitazione, in cui fanno la loro comparsa i famosi spazi-tempi curvi) propose a un ambiente scientifico che di lì a poco avrebbe seguito istupidito l'ultimissima moda lanciata dai cosiddetti "mandarini" della scienza fisico-matematica, per la maggior parte tedeschi collegati ancora una volta all'ambiente di Göttingen:

<<The views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength. They are radical. Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality>>⁴⁶.

Parole rimaste giustamente celebri (ma per noi famigerate), che da un canto convincevano i fisici mediante il richiamo al prestigio della matematica (che i fisici conoscono in genere poco), dall'altro costringevano i matematici ad accogliere la necessità di certe modifiche fondazionali, sgradite ai più, a causa di non ben precisati risultati sperimentali, di cui la maggioranza non sapeva nulla (e che comunemente i "non esperti" tendono ad accettare come indiscutibili "dati di fatto" - e potrebbe essere altrimenti dopo il "caso Galileo"?! - ignorando quanto essi possano invece essere fraintesi, o manipolati⁴⁷: un esempio altamente istruttivo, una critica al famoso esperimento degli "orologi in volo", che avrebbe confermato le previsioni relativistiche, si trova in: http://www.dipmat.unipg.it/~bartocci/H&KPaper.htm). Si tratta di un punto che andrebbe profondamente sviscerato: a quali esperimenti si riferiva Minkowski, nell'estrema penuria che all'epoca regnava al riguardo? Incomprensioni, errori, in qualche caso veri e propri "imbrogli", e non è assurdo pensare che le successive acquisizioni sperimentali siano state "interpretate" alla luce del nuovo "paradigma", che man mano soppianterà tutti i rivali⁴⁸.

Ammettiamo che il concetto di spazio-tempo di Minkowski possa essere anch'esso un "modello" utile per inquadrare determinati fenomeni, ma non certo una descrizione "adeguata", sia pure parzialmente, della realtà. E fin qui si troverebbe magari un alto grado di consenso, però lo scetticismo scientifico novecentesco non si accontenta di tale ovvietà, ed erge quell'utilità a una sorta di moderno nec plus ultra per il giudizio della voluntas. Questa, per il tramite dell'intelletto, non può che elaborare "modelli", in larga misura perfino contraddittori, e la selezione che si può effettuare tra di essi ha per unico criterio un'eventuale loro dimostrata "efficacia pratica", e "predittiva", che ne condiziona la sopravvivenza (un'eco della selezione naturale darwinista applicata alle teorie scientifiche!), intesa come accettazione da parte della "comunità scientifica", un altro termine "astratto", dietro il quale si nascondono talvolta alcune nefandezze.

Si comprende bene allora, si spera, perché abbia stentato secondo noi a farsi strada un'interpretazione rigorosamente dualistica del tipo da noi proposto, quando tutto lo sviluppo della matematica e della fisica moderna, sin dalle origini, è stato largamente anti-dualistico (i.e., riduzionista). Chissà per esempio che l'opinione di H. Weyl riportata nel paragrafo 6 non sia stata influenzata proprio dalla sua devozione per la teoria della relatività, nei cui confronti esprime inequivocabili accenti di entusiasmo: <<Einstein's Theory of Relativity has advanced our ideas of the structure of the cosmos a step further. It is as if a wall which separated us from Truth has collapsed>> (dall'introduzione della sua importante opera Raum-Zeit-Materie, J. Springer, Berlin, 1918)⁴⁹.

In tale contesto, ci piace rispondere a priori pure a chi sostenesse, e sono stati tanti nel corso degli anni, che le nozioni da noi utilizzate (intuizione, forme pure, spazio ordinario, retta temporale, etc.) non gli appaiono chiaramente "definite", e sono state quindi giustamente "sorpassate". Facciamo vedere in un caso paradigmatico come siano viceversa più chiare quelle moderne! Ecco cosa è costretto a dire un giovane fisico (cui va tutta la nostra comprensione), per spiegare a sua volta ad altri ciò che gli è stato insegnato.

<<In effetti, già la teoria della gravitazione universale di Newton proponeva un modello cosmologico molto semplice ed efficace, il primo modello cosmologico su basi scientifiche dell'umanità, che però porta a paradossi ineliminabili. Secondo il modello newtoniano il tempo è infinito e lo spazio è infinito ed è riempito uniformemente di stelle e pianeti. Con questi presupposti, per esempio, il cielo di notte dovrebbe essere luminoso (la luce dovrebbe provenire da ogni parte dell'universo da sempre e quindi essere infinita). Per gli stessi motivi, il campo gravitazionale in un punto dovrebbe essere infinito. Naturalmente tutto ciò non si verifica per cui la cosmologia newtoniana va corretta radicalmente. La Relatività Generale fornisce queste correzioni e con essa è possibile fare considerazioni sulla geometria dell'universo perché questa teoria è in effetti una teoria geometrica. Essa afferma in sostanza che la geometria dello spazio è prodotta dalla distribuzione delle masse. Lo spazio, ed anche il tempo, non sono entità astratte esistenti a priori, come nella teoria newtoniana, ma sono prodotti dai corpi>>⁵⁰.

Dotare di significato, sia pure in maniera approssimativa, quel <<prodotti dai corpi>>, è impresa che supera le forze di chicchessia. Bello è in ogni caso pensare a un tempo che viene prodotto come un fluido dalla Terra, mentre un altro (omogeneo al primo?) viene prodotto dal Sole, e poi ai due che si fondono insieme (ma nella relatività, peggio se "generale", non c'è nessun "tempo", almeno nell'accezione ordinaria del termine, cui i fisici sono comunque costretti a ricorrere quando cercano di fare opera di "divulgazione").

9. Un excursus speculativo sulla struttura della res extensa

Quello di cui abbiamo discusso, additandolo quale soluzione dei paradossi di Zenone, è un dualismo interno al pensato (ed è nel pensato che comunque ogni riflessione gnoseologica va a collocarsi: addirittura nel "parlato" quando, come adesso, la si comunichi ad altri - vedi la nota 8), termine che a sua volta è componente essenziale dell'altro dualismo pensato/reale. Vogliamo adesso speculare un po' sul "reale", per accennare alla possibilità che non sia il modello discreto del tempo a essere non adeguato in questo discorso, bensì proprio il modello continuo dello spazio (indubitabilmente, però, alla base della concezione mentale di esso). Volendo fare una congettura sulla costituzione della res extensa (che, essendo una, potrà avere una sola delle antitetiche caratteristiche: continuo o discreto⁵¹ - o forse nessuna di esse?!), appare plausibile innanzitutto scartare lo spazio vuoto newtoniano (ripreso poi dalla relatività ristretta di Einstein), e proporre una teoria dello spazio fisico come oggetto materiale dotato di ben precise proprietà (teoria dell'etere), unica strada capace di conferire razionalità (causalità inclusa), alla filosofia naturale. Un etere che però non sia concepito nella veste di nuovo "contenitore" sostanzialmente inerte, bensì in modo dinamico, parti del quale si muovono "collettivamente" rispetto ad altre. Di tale etere avanzare poi l'ipotesi di una struttura granulare, e quindi essenzialmente discreta (quantizzata), una sorta di "pulviscolo" agitato da un perenne movimento di tipo browniano (con velocità scalare che in prima approssimazione si può supporre costante, e dell'ordine di grandezza della famosa "costante universale", la velocità della luce c). Naturalmente, non è possibile concepire nell'intelletto fenomeni del genere se non immergendo il tutto in uno "spazio vuoto" che funga lui, ma solo nella nostra mente, da "contenitore" ideale. Uno spazio "reale" (non lo "spazio reale" dei matematici, costruito sul concetto "ideale" di numero reale, cfr. la nota 45) interamente "materiale", l'autentica res extensa, il cui aspetto energetico sarebbe riconducibile esclusivamente al moto. Però la materia "vera" (quella che riconosciamo tale, la materia dotata di massa, che possiamo chiamare allora "materia pesante") dovrebbe concepirsi in modo da permettere di distinguere un "corpo" dalle diverse "monadi d'etere" che gli stanno intorno. Una singola "particella" materiale, costituente primitivo (elementare) della materia pesante (che risulterà un aggregato di tante di esse), si potrebbe immaginare come una monade confinata in un moto circolare, che mantiene una sua precisa "identità", e, pur movendosi sempre, apparirebbe in qualche caso "ferma" (fisso cioè il suo centro ideale di rotazione - vuoto?!). Il raggio r del moto circolare in oggetto (comunque un multiplo intero di l , l'"estensione" da attribuire a una monade d'etere) sarebbe proporzionale alla "massa inerziale" della particella, e pertanto all'origine della sua capacità di provocare "effetti gravitazionali" (attrattivi) su altre particelle, e di subirne a sua volta. Questa è manifestamente una naturale versione aggiornata dell'atomismo democriteo⁵², di cui si possono trovare sviluppi nel saggio "Ipotesi dell'etere nella vita dell'universo" (1903), di Olinto De Pretto⁵³.

Nota. In un simile modello bidimensionale⁵⁴ c'è da aspettarsi un'asimmetria delle interazioni tra particelle elementari, tanto più spiccata quanto minore è la temperatura dell'ambiente ("fusione fredda"?!), e quindi presumibilmente ridotta la prevedibile ulteriore rotazione intorno a un diametro (variabile) della circonferenza su cui avviene il moto della monade d'etere - rotazione che tramuterebbe a tutti gli effetti la "forma" della particella in quella di una "piccola sfera". Ci sembra interessante aggiungere che la descrizione proposta sembra in grado di interpretare un'eventuale "dilatazione del tempo", esattamente negli stessi termini della teoria della relatività ristretta (un'altra spiegazione, concernente lo sperimentato aumento della "vita media" di particelle in movimento veloce rispetto alla Terra, la si può trovare nel paragrafo 3 di "Looking for Special Relativity's Possible Experimental Falsifications", del presente autore, Episteme N. 6, Parte II, a riprova della tesi che un medesimo "dato di fatto" si possa prestare a interpretazioni diverse). Si tratta di un'osservazione che ci viene dal noto fisico teorico Giancarlo Cavalleri. Se supponiamo che la velocità scalare assoluta della monade "imprigionata" nella particella elementare sia sempre c, come per le monadi in movimento lineare, sia che la particella stia ferma, sia che si muova rispetto allo spazio (al complesso delle altre monadi vibranti), diciamo con una certa velocità scalare v, ecco che si ha:

1 - caso della particella ferma, raggio del moto rotatorio r, velocità angolare w = c/r, periodo T (simbolo tradizionale, che non ha nulla ovviamente a che fare con quello prescelto per la retta temporale!) T = 2p /w = 2p r/c, frequenza n = 1/T;

2 - caso della particella in moto (elicoidale), con componente traslatoria v, raggio ancora r, nuova velocità di rotazione c' = w 'r, tale che (c')²+v² = c² (la velocità scalare totale deve rimanere c). Da qui si trae: (w 'r)²+v² = c², ovvero: (w ')² = (c²-v²)/r² = w ²-w ^{2b 2} = w ²(1-b ²) (dove b è il classico simbolo per il rapporto v/c), ossia: w ' = w, e quindi il nuovo periodo è: T' = 2p /w ' = 2p /(w) = Tg (g è l'usuale simbolo per l'inverso del fattore ), mentre per la nuova frequenza risulta in conformità: n ' = 1/T' = n, come volevasi dimostrare. Vale a dire, un "osservatore" in moto con la particella, che misurasse il proprio tempo in base ai ritorni periodici di essa sul punto di partenza del moto rotatorio, riscontrerebbe un rallentamento del tempo, nella proporzione determinata, nei confronti di un osservatore fermo, che misurasse il tempo rispetto a una "stessa" particella però solidale con lui. [Quanto precede vale ovviamente a rigore solo per un moto perpendicolare all'orbita della monade; in altri casi si potrebbero avanzare delle considerazioni "di media".]

La fisica quantistica moderna⁵⁵ fornisce alcuni valori numerici che danno informazioni sui possibili ordini di grandezza qui in gioco. Li riassumiamo di seguito a beneficio dei lettori, sperando di non incorrere in sviste in un campo in cui non siamo "esperti". Si introduce una lunghezza di Planck (quanto di spazio), diciamola l , dell'ordine di 10^-35 metri, che nella nostra concezione potrebbe essere connessa alla dimensione della monade d'etere, cioè del vero atomo. In corrispondenza si definisce un tempo di Planck (quanto di tempo, o cronone), per il quale usiamo (ancora) il simbolo t , mediante la formula l /t = c, dove c è la "costante" che esprime la velocità della luce. [Ribadiamo che sia il quanto di spazio sia quello di tempo sono enti del tipo che abbiamo denominato "segmenti", e non punti, o istanti.] Ammessa per questa velocità un ordine di grandezza di 10⁸ metri al secondo, ecco che il quanto di tempo verrebbe ad avere un valore di circa 10^-43 secondi. Diamo qualche esempio per poter operare meglio un "confronto" con tali numeri piccolissimi, del tutto al di fuori della nostra esperienza ordinaria - ciò nonostante, si può rimanere fedeli al principio che così come è comprensibile il grande, altrettanto deve essere comprensibile il piccolo, con i medesimi strumenti concettuali, e spiegazioni per analogia: <<Ordo et connectio idearum idem est ac ordo et connectio rerum>> (Baruch Spinoza, Ethica ordine geometrico demonstrata, 1675, Parte II, Prop. 7). Per il raggio di un atomo (nel senso corrente del termine) si dà un ordine di grandezza pari a 10^-11 (sempre metri), mentre per il nucleo di un atomo si propone 10^-14, cioè un ordine di grandezza mille volte più piccolo. Le particelle che compongono il nucleo verrebbero ad avere una dimensione che è circa la decima parte di questo valore, cioè 10^-15. Per ciò che concerne il tempo, le particelle con "vita" più breve durano intorno ai 10^-23 secondi. Il miliardesimo di secondo, cioè 10^-9 sec, appare invece una stima corretta per il minimo atto di elaborazione di uno dei computer attuali⁵⁶ (si può forse dimezzare, o dividere per 4, in presenza di macchine più avanzate in dotazione a enti di ricerca o militari, comunque non meglio di 10^-10). Quindi siamo in tutti i casi ancora lontanissimi dagli ordini di grandezza proposti per la monade d'etere, e per il quanto di tempo.

Tornando alla nostra questione, al trascorrere di un quanto di tempo (o di un cronone, o anche di un clic, termine che abbiamo introdotto nel paragrafo 5, e che qui starebbe per il segmento minimo della retta temporale), data l'identità l /t = c, solo la luce si è mossa di un quanto di spazio. Possiamo pensare, come detto, che la stessa cosa si verifichi sia per le monadi d'etere in vibrazione lineare incessante, sia per quelle che costituiscono la "materia pesante", che orbitano intorno a un punto. C'è da chiedersi allora cosa accade per velocità minori di c, che competono a una delle descritte particelle elementari, o a un corpo macroscopico materiale. La risposta obbligata è: tutto sta fermo. Ossia, quando è trascorso un cronone, un "corpo" che si muove a velocità v < c non si è spostato in realtà neppure di un quanto di spazio (anche l'immaginare i corpi come a enti "puntiformi" rimanda al dualismo reale/pensato). Solo dopo un certo numero intero N di "quanti" t , si ritrova uno di questi oggetti "improvvisamente" spostato da una posizione (da un "luogo") a un'altra, senza che esso abbia potuto attraversare alcuna delle posizioni intermedie, né quelle pensabili, né quelle effettivamente occupabili. Ci si può domandare anzi se a spostarsi nello spazio siano proprio le monadi d'etere (o la monade d'etere, se si considera una singola particella elementare) che costituiscono il corpo mobile, o se a spostarsi sia soltanto la "struttura" di moto ("campo di velocità") caratterizzante l'oggetto, così come accade per le onde. Si potrebbe pensare in tale caso che il tempo Nt sia necessario perché l'intera struttura di moto di un corpo si possa trasferire in una zona adiacente, e lì ricostituirsi completamente ma con differenti monadi d'etere⁵⁷.

Siffatte speculazioni (più o meno fantasiose) presentano un evidente legame con un terzo paradosso di Zenone, cosiddetto "della freccia", di cui non abbiamo fatto fin qui menzione (tranne che nell'epigrafe). Aristotele ne riferisce nel seguente modo (loc. cit.): <<Finché una cosa sta in uno stesso spazio è in riposo. Ma la freccia che vola è in ogni istante in uno stesso spazio. E' in riposo, quindi, in ogni istante del suo volo; perciò anche durante tutto il volo il suo movimento è solo apparente>>. In effetti, tra un clic e il successivo (è esattamente il caso di dire, in ossequio alla struttura discreta del tempo che stiamo ipotizzando), la freccia rimane ferma nel luogo che occupa, ma ciò non significa che non esista il movimento come fenomeno globale: al succedersi inesorabile dei clic (ripetiamo: tempus edax rerum) la troviamo infine spostata⁵⁸.

Nota. Si potrebbe dire qualcosa in più su quella pretesa costante universale c che abbiamo anche noi utilizzato. Conformemente ai principi ispiratori di una teoria dell'etere, si deve pensare che essa corrisponda a una velocità caratteristica di propagazione di "onde" nel mezzo (per esempio elettromagnetiche, ma non si può escludere che ne esistano anche altre di differente natura - pure longitudinali, e non solo trasversali - con diversa velocità di propagazione). Una velocità che quale velocità cinematica è uguale a c solo rispetto un osservatore solidale con il mezzo (che usi un orologio "ragionevole"), in una sua regione "uniforme", e non rispetto a un osservatore in movimento esso stesso nel mezzo (cioè, nessun "principio di relatività", nessuna invarianza della velocità della luce rispetto a osservatori "inerziali", il che riporta in qualche modo al quarto paradosso di Zenone, di natura diversa dagli altri tre: se è concepibile una velocità massima rispetto al mezzo, che si dice allora assoluta, quale appunto la c, una velocità relativa può arrivare a essere il doppio di c). Come si sa, nell'elettrodinamica di Maxwell tale costante c è descritta mediante la formula 1/, dove e ₀ e m ₀ sono due "costanti" caratteristiche del mezzo, che dobbiamo però immaginare assai più verosimilmente variabili, da una regione all'altra dello spazio, in funzione di una "densità" che non è obbligatorio pensare sempre uguale. Per esempio, si avrebbe un certo valore di c in presenza di significativi campi gravitazionali, ossia di grandi masse, come qui sulla Terra, e uno differente negli spazi interstellari (dove sarebbe lecito congetturare che la luce viaggi molto più lentamente), con la conseguenza che se si usassero strumenti di misura del tempo del tipo di quei light-clock descritti nel citato paragrafo 3 di "Looking for Special Relativity's...", ci sarebbe da aspettarsi un fenomeno niente affatto assurdo di "variabilità del tempo" da un punto all'altro dell'universo (ma, sottolineiamo, del tempo "misurato", che potrebbe anche dipendere dal tipo di orologio impiegato!).

Insomma, c'è abbastanza "spazio", è proprio il caso di dire, per parecchie non inutili speculazioni, lungo strade finora non esplorate quanto meriterebbero, che potrebbero riservare nuove sorprendenti scoperte (pure "applicative").

10. Conclusione

Riassumendo. I paradossi di Zenone non possono essere "risolti", può esserne solo spiegata la "radice". Riguardano le modalità con cui funziona la nostra mente ("giuste" o "sbagliate" che siano⁵⁹). Additano, in perpetuo, un'antinomia della ragione pura, un ostacolo che essa è costretta a superare ogni volta che cerchi di concepire esattamente qualsiasi forma di movimento. Costituiscono uno spunto di meditazione per il riconoscimento del fatto che tempo (retta temporale) e spazio (retta geometrica) si intuiscono in modi inconciliabilmente differenti. Il movimento esiste nella realtà, e in quanto tale non implica alcuna contraddizione: esso è, semplicemente, come intendeva Diogene. Altra cosa è l'immagine del movimento nell'intelletto, che deve di necessità utilizzare entrambe le forme pure, spazio e tempo, unendole in una sintesi provvisoria ma intimamente contraddittoria. La seguente tabella corrisponde alla concezione dello spazio e del tempo, "reali" e "ideali", che qui è stata delineata⁶⁰:
 
 

I paradossi hanno anche il merito di farci comprendere la differenza kantiana tra fenomeno e noumeno, o tra pensato e reale. La "realtà materiale" è una sola, ma è inimmaginabile fino in fondo nel suo divenire. Tra un clic e l'altro del tempo (del fluire della coscienza) è come se essa cessasse di esistere, per poi riemergere dal "nulla", ripresentandosi alla nostra contemplazione in uno "stato" diverso dal precedente, seppure ad esso causalmente collegato.
 
 

1 - Nato intorno al 500 AC, fu discepolo del famoso Parmenide, pure di Elea (colonia della Magna Grecia situata sulla costa tirrenica, nella parte meridionale della Campania, a sud di Paestum, in provincia di Salerno).

2 - Silvia Clara Roero, Tullio Viola: "I paradossi di Zenone sul movimento", Rendiconti Seminario Matematico Università Politecnico di Torino, 34, 1975-76.

3 - William I. McLaughlin, "La risoluzione dei paradossi di Zenone sul moto", Le Scienze, N. 317, 1994, pp. 60-66.

4 - Si veda quanto si dice a proposito di "cattivi maestri" nel punto 8 della pagina:
http://www.dipmat.unipg.it/~bartocci/listamat.htm. Per quanto riguarda il caso specifico, citiamo da http://plato.stanford.edu/entries/paradox-zeno/ un commento che giustamente ridimensiona il proclama in oggetto: <<And it has been shown by McLaughlin (1992, 1994) that Zeno's paradoxes can also be resolved in non-standard analysis [...] It should be emphasized however that -- contrary to McLaughlin's suggestions -- there is no need for non-standard analysis to solve the paradoxes: either system [standard mathematics] is equally successful>>. Il riferimento è naturalmente alla pseudo-soluzione di cui ci occuperemo nel paragrafo 4.

5 - Per esempio, nel suo interessante Modern Science and Zeno's Paradoxes (Wesleyan University Press 1967; 2^nd edition Allen and Unwin, London, 1968), il noto filosofo della scienza Adolf Grünbaum scrive: <<I shall deal critically with Zeno's Dichotomy and Achilles paradoxes in the context of modern kinematics without any historical regard to what their intent might have been>>.

6 - Una breve osservazione sull'ordine con cui introdurre i due termini, ineludibile quando ci si esprime nel tempo (chi legge, secondo le nostre convenzioni, legge la "prima" parola - o lettera - in alto a sinistra, seguita da una ben precisa "seconda", etc.), che è il supremo ordinatore. Cioè, chi deve essere nominato innanzitutto, il continuo o il discreto? Nell'appendice abbiamo messo al primo posto la nozione più semplice dal punto di vista matematico, ossia il discreto, ma osserviamo che abitualmente si parla di spazio-tempo e non di tempo-spazio. Tale scelta, ancora una volta (vedi il paragrafo 7), non ci appare irrilevante, laddove molti alzerebbero invece le spalle, sbuffando: "quante pedanterie, è la stessa cosa". Al contrario, abbiamo conosciuto valenti fisici-matematici che sostenevano che il tempo fosse la cosa maggiormente rilevante, in quanto collegato allo "spirito", e di conseguenza scrivevano la metrica lorentziana dello spazio-tempo della relatività ristretta nella forma meno comune dt²-dx²-dy²-dz², anziché in quella tradizionale, e invero più semplice, dx²+dy²+dz²-dt².

7 - Sulla limitatezza/illimitatezza dell'universo nello spazio e nel tempo; sull'esistenza/inesistenza di "sostanze semplici"; sulla necessità o meno di una causa libera nel mondo; sull'esistenza/inesistenza di un essere assolutamente necessario. Va da sé, attualmente "antinomia" non è intesa nel senso comune di "contraddizione logica", né si tratta di un dualismo che possa risolversi in una "sintesi", che mantenga parte della tesi e dell'antitesi, armonizzando la loro unione in una nuova tesi (per esempio, questo articolo, ma ancora più il progetto di cui alla nota 9, potrebbero essere definiti tentativi di sintesi, tra la "mathesis perennis" e la matematica contemporanea formalista). Invece, i due "corni" delle antinomie qui in esame restano irrimediabilmente contrapposti.

8 - Si rammenta con riconoscenza l'articolo di Franco Palladino, "I paradossi eleatici e la matematica moderna" (Periodico di Matematiche, 1982), che per primo introdusse lo scrivente alla fondamentale tricotomia reale-pensato-parlato, e alla sua rilevanza per la comprensione delle origini del pensiero greco, così influendo in maniera determinante sul successivo sviluppo del percorso intellettuale che lo ha condotto alle idee qui illustrate. Citiamo dall'introduzione del lavoro alcune righe che a distanza di anni continuiamo a trovare illuminanti: <<non per il gusto di fare "archeologia delle scienze" ma perché la "filosofia eleatica", espressa da Parmenide e Zenone, rappresenta un passaggio obbligato per una lucida comprensione dei rapporti tra concreto e astratto, empirico e razionale, discreto e continuo>>.

9 - Notiamo che già qui abbiamo a che fare con un complesso di concetti "astratti", ossia "ideali", l'introduzione di ciascuno dei quali meriterebbe un'adeguata presentazione (a cui stiamo cercando di provvedere con un progetto di Elementi di Matematica in rete, secondo una prospettiva "kantiana": http://www.dipmat.unipg.it/~bartocci/mat/elementi.htm).

10 - Che non si limita solo a riportare gli argomenti di Zenone ma pure a criticarli, probabilmente facendo sì, con la sua indubbia autorità, che la relativa discussione sia stata condizionata per secoli dall'impostazione da lui proposta. Con il declino della cultura greca, un lungo silenzio finì poi con l'avvolgere l'intero problema, fino alla ripresa dell'interesse in tempi moderni (cfr. anche quanto si dice nel paragrafo 8 su Zenone e gli Arabi). Non ci addentriamo qui in un'analisi delle critiche aristoteliche, perché confessiamo di trovarle nel complesso piuttosto oscure. Ci sembra però che esse possano sintetizzarsi nell'affermazione dell'esistenza di un "isomorfismo" tra tempo e spazio (vedi il paragrafo 6): <<risulta necessario che anche il tempo sia continuo>> (Fisica, VI, 4). Altra nostra divergenza con Aristotele, è che il tempo non appare indissolubilmente legato al divenire della res extensa (il movimento, o il cambiamento), bensì a un fenomeno di natura spirituale, la "durata" dell'umana coscienza (caratterizzata in senso cartesiano dal pensiero - sulla questione ritorneremo al termine del paragrafo 7).

11 - Nel nostro caso, possiamo identificare nel termine "grandezze" i segmenti (propri, ovvero, non ridotti a un singolo punto, o, come si dice anche, non degeneri) della retta ordinaria. E qui v'è luogo per una precisazione su una circostanza che induce diverse persone in errore. L'indubbia circostanza che un segmento sia costituito di tanti elementi indivisibili, i suoi punti, nulla toglie al fatto che esso si possa suddividere all'infinito in segmenti più piccoli, i quali non sono mai punti, allo stesso modo che i punti non sono mai segmenti (secondo Aristotele invece: <<è impossibile che qualcosa di continuo risulti composto da indivisibili, ad esempio che una linea risulti composta da punti, se è vero che la linea è un continuo e il punto è un indivisibile>>, Fisica VI, 1). Insomma, non bisogna confondere i punti con i segmenti, e l'obiezione che una "somma" di infinite "grandezze" che hanno misura zero (volendo includere in questo caso pure i punti) dovrebbe ancora costituire una grandezza di misura zero, ciò che non accade certo per i segmenti, trasferisce indebitamente la proprietà additiva delle misure dal caso finito al caso infinito (più o meno la medesima cosa quando si discuteva sull'infinito come "numero", domandando allora se esso fosse pari, o dispari), dove qualsiasi nuova caratteristica è sempre tutta da accertare (per esempio, introducendo anche la differenziazione ben nota di origine cantoriana sul "tipo" degli infiniti di cui trattasi). Un insieme costituito da un numero finito di punti ha precisamente misura zero, come è lecito aspettarsi, pretendere.

12 - Non sono in realtà proprio il medesimo concetto: preferiamo vedere nel secondo termine cartesiano lo "spirito", che consideriamo distinto dall'intelletto, mentre quest'ultimo fa sempre parte in qualche modo della "realtà materiale" (assieme alla funzione memoria), cioè della res extensa. Comunque sia riteniamo che, in prima approssimazione almeno, si comprenda di cosa si sta parlando.

13 - La circostanza che mezzo passo non sia un passo riporta alla mente il bambino del famoso giudizio di Salomone: mezzo bambino non è un bambino, e non accontenta nessuna delle due pretese madri. Ecco un altro esempio di un "uno" indivisibile, come l'unità dei numeri naturali, mentre non accade altrettanto per l'unità dei numeri razionali, o reali.

14 - Che alcuni chiamano "spazio euclideo", in quanto fu descritto nel III secolo AC da Euclide nei suoi celebri Elementi. Meglio è senz'altro dire però "spazio ordinario", così come "geometria intuitiva" appare preferibile a "geometria euclidea", naturalmente a meno che non si stia facendo esplicita opera di esegesi del testo euclideo.

15 - Per confutare le tesi di Zenone contro l'esistenza del movimento, Diogene si sarebbe semplicemente alzato, e messo a camminare (solvitur ambulando!). Secondo un'altra tradizione, sarebbe stato invece il maestro di Diogene, Antistene di Atene, a sua volta un discepolo di Socrate, a passeggiare nervosamente intorno a Zenone, al punto che questi avrebbe esclamato: "Ma la finisci di andare avanti e indietro!", al che Antistene avrebbe risposto, lieto di constatare che la sua provocazione aveva avuto successo: "Vedi allora che credi anche tu al movimento?".

16 - Ciò che rimanda alla tricotomia citata nella nota 8. Il linguaggio è peraltro legato al tempo, e all'ordine da esso "imposto", come si accennava nella nota 6. Il pensiero, più complesso del linguaggio, viene da alcuni filosofi indebitamente ricondotto nell'ambito di quest'ultimo.

17 - <<La scienza matematica era ancora per lui alquanto oscura. [...] Oh, Zenone, Zenone, povero vecchio diavolo, non conosci il Kowalewski?>>. Questi versi sono riportati in Herbert Meschkowski, Mutamenti nel pensiero matematico, Boringhieri, Torino, 1973, p. 41 (il testo completo della poesia si può trovare in http://www.hirnwindungen.de/Mathe/hirn_griech_math.html). Il riferimento al Kowalewski (Gerhard K., un allievo di Sophus Lie, laureato in matematica a Lipsia nel 1898) allude al trattato Die Klassischen Probleme der Analysis des Unendlichen, Leipzig, 1921.

18 - Questa "intuizione" è un dato di fatto che deve essere considerato sostanzialmente immutabile secondo la filosofia che qui ci guida, almeno finché tale resterà la manifestazione dell'umano quale noi lo conosciamo (vedi anche quanto se ne dirà nel paragrafo 6). L'adesione all'opinione in parola, o alla sua negazione, costituisce una discriminante fondamentale per ogni sistema di pensiero, ed è chiaro che, come abbiamo in diverse occasioni avuto modo di sottolineare, l'influenza del darwinismo è stata decisiva per la drammatica riduzione del numero delle persone che fanno della prima alternativa il fondamento della propria Weltanschauung.

19 - Infinito attuale o potenziale che voglia dirsi, sempre di infinito si tratta (si rammenti il II postulato di Euclide, che "risolve" il problema della definizione di retta con un'ammissione della possibilità di prolungabilità "indeterminata" di un segmento). Del resto, noi non siamo di quelli che si fanno tanto scrupolo ad accettare la presenza dell'infinito attuale in numerosi ragionamenti di matematica, in accordo (tranne la parte finale!) con la posizione espressa da Leibnitz: <<Je suis tellement pour l'infini actuel, qu'au lieu d'admettre que la nature l'abhorre, comme l'on dit vulgairement, je tiens qu'elle l'affecte par-tout, pour mieux marquer les perfections de son Auteur>> (Opera omnia studio Ludov. Dutens, Tomo II, parte I, p. 243; citato in epigrafe all'opera di Bolzano di cui alla nota 34).

20 - Usiamo questo termine anche se non è detto che una concezione atomistica quale quella che stiamo illustrando sia necessariamente "materiale". Tale è per esempio secondo noi, come diremo, la descrizione più adeguata della "retta temporale" dell'intuizione ordinaria, che non ha appunto nulla di materiale.

21 - Vedi però anche quanto secondo noi più convincentemente ne dice T. Viola, nel paragrafo 6.

22 - Tali parole ribadiscono ovviamente la convinzione dell'autore che la distanza tra i sistemi di Cartesio e Kant non sia poi così eccessiva, e che si possa fondare un "nuovo" sistema unendo parti dei due, oltre naturalmente a quanto di nuovo e accettabile si è venuto aggiungendo nel corso dei secoli (un'opinione questa che ci è capitato di vedere spesso aspramente rimproverata!).

23 - In termini "tecnici" attuali, condizione necessaria perché una serie numerica (e intendiamo pure per semplicità con elementi tutti positivi) risulti convergente è che il suo "termine generale" sia infinitesimo, diventi cioè sempre più piccolo andando avanti nella successione dei termini. In una serie di segmenti temporali, il termine generale non appare invece infinitesimo. Val la pena sottolineare che quella detta è una condizione necessaria, appunto, ma non sufficiente, come dimostra il famoso caso della serie armonica 1+1/2+1/3+1/4+..., che è divergente nonostante il suo termine generale 1/n sia palesemente infinitesimo, al crescere di n (si veda la chiara spiegazione che se ne dà in http://www.mclink.it/personal/MC5834/anpag78.htm).

24 - I punti in Euclide sono concepiti come "segni", o "graffiti", sulla retta. La primissima delle sue definizioni recita infatti: <<Un punto [s h m e i o n ] è ciò che non ha parti [o u m e r o V o u q e n , letteralmente: dove parte nessuna]>>.

25 - Il Dizionario Enciclopedico Italiano (1970), alla voce "continuità", riporta: <<In filosofia, il termine designa ciò la cui percezione non si lascia scindere in tante percezioni elementari distinguibili l'una dall'altra>>.

26 - A chi sostiene il contrario, credendo di avere risolto la questione della "quarta dimensione" semplicemente perché sa banalmente estendere la manipolazione di coppie o terne ordinate di numeri reali a quaterne etc. ordinate degli stessi numeri reali, basta chiedere se è in grado di "vedere" quanti spigoli, o facce, possiede un ipercubo a n dimensioni (n > 3), o di offrire una spiegazione del fatto che il volume dell'ipersfera di raggio 1 presenta il bizzarro noto comportamento (il suo volume aumenta fino alla dimensione 6, per poi cominciare a diminuire e tendere addirittura al limite zero al crescere della dimensione; insomma, tale ipersfera diventa sempre più piccola, e non, come sarebbe forse stato lecito aspettarsi da un punto di vista "intuitivo", sempre più grande).

27 - Qui si presenta uno di quegli sgradevoli conflitti linguistici già portati all'attenzione del lettore, e al quale vogliamo apertamente accennare. L'autore ha sovente parlato di "irrazionalità" nella fisica (vedi ad es. la nota 19 in http://www.dipmat.unipg.it/~bartocci/falsper.html, o il preambolo a "Conoscenza e potenza" in questo stesso volume), mentre adesso si nomina una razionalità della matematica, anche nel momento in cui fornisce modelli (pertanto razionali) a una fisica irrazionale! Sottolineiamo ancora una volta che una teoria fisica può essere definita "irrazionale" (cosa ben diversa da non conforme alla realtà: possono darsi teorie fisiche razionali nel nostro senso, quindi intrinsecamente coerenti, che siano però completamente "sbagliate") non quando è logicamente assurda, i.e. auto-contraddittoria, ma semplicemente quando non è capace di costruire le sue spiegazioni facendo unico ricorso all'intuizione, o razionalità ordinaria (servendosi cioè come elementi base di: spazio, tempo e causalità, nell'accezione "comune" dei termini). Una distinzione che andrebbe evidenziata mediante l'uso di altre più adeguate espressioni (da "inventare"), l'importante è capirsi, sia pure non "immediatamente".

28 - Appare qui appropriato un rimando alla discussione sul "pitagorismo" contenuta in "Il linguaggio della matematica" (Umberto Bartocci e Rocco Vittorio Macrì, Episteme N. 5).

29 - Bisogna riconoscere a questo proposito che in realtà il linguaggio comune utilizza espressioni quali "pensiamoci un istante", con ciò confondendo, a nostro parere, la "monade di tempo" con il minimo segmento t della retta temporale, che di istanti ne deve contenere due, i suoi estremi, che indicano l'inizio e la fine di qualsiasi "atto", compreso quello del pensare. Ribadiamo che, secondo le "convenzioni descrittive" da noi illustrate, non si può effettuare la misura di un segmento temporale s rispetto a un intervallo chiuso improprio w , consistente di un unico istante. Infatti, malgrado venga voglia di considerare il numero di istanti n da cui è formato s come il risultato di tale misura, la somma w +w +... n volte fa sempre w , e non s . Insomma, w corrisponde piuttosto allo zero, che non all'uno (si rammenti quanto se ne diceva poc'anzi, nel punto 5, e soprattutto nella nota: investigazione delle leggi dell'intelletto). Sottolineiamo anche che non vorremmo che l'esempio in oggetto ci portasse in una direzione impervia che a nessuno è dato veramente di poter chiarire, il passaggio cioè dal pensato al reale, l'oggettivazione del tempo attraverso uno strumento di misura fisico. Per il tempo non è possibile introdurre un "campione" rigido, immutabile, che sia immaginabile conservare in qualche museo. Nessuno sarà mai in grado di garantire che un secondo misurato oggi sia identico a un secondo misurato ieri, sia pure dallo stesso orologio, ma lasciamo stare siffatto tipo di argomentazioni comunque interessanti, ripetendo che si può parlare solo del tempo pensato, esclusivamente quindi di una forma pura dell'intelletto (vedi ancora sull'argomento il paragrafo 9).

30 - Al medesimo argomento presta attenzione Hermann Weyl (nel suo comunque interessante Filosofia della matematica e delle scienze naturali, 1949; ed. it. Boringhieri, Torino, 1967) con le seguenti parole (alquanto vicine all'interpretazione che qui propugniamo, anche se non viene fatto cenno esplicito al dualismo spazio-tempo, e si confonde il piano del pensato con quello del reale): <<L'osservazione che le successive somme parziali della serie [...] non crescono oltre ogni limite, bensì convergono [...] (che è l'osservazione con cui oggi si risolve il paradosso), è certamente pertinente e chiarificatrice. Cionostante, se il segmento di lunghezza 1 dovesse consistere realmente di segmenti parziali di lunghezza 1/2, 1/4, 1/8,..., a modo di unità "staccate", in tal caso l'idea che l'Achille possa attraversarli tutti sarebbe incompatibile con la natura dell'infinito inteso come "incompletabile". Ma se si ammette questa possibilità, non vi sono ragioni perché una macchina non debba essere in grado di eseguire in un intervallo finito di tempo una successione infinita di atti di decisione distinti: per esempio, dando il primo risultato dopo 1/2 minuto, il secondo 1/4 di minuto dopo il primo, il terzo 1/8 di minuto dopo il secondo, ecc.>> (pp. 50-51).

31 - Precisamente, da quando un gruppo di matematici con smanie di innovazioni fondazionali volle proporre un'azzardata interpretazione filosofica della possibilità razionale di geometrie "non euclidee", introdotte senza sconvolgere nessuno una quarantina di anni prima. Un termine a quo potrebbe essere fissato nel 1871, corrispondentemente alla pubblicazione di "Ueber die sogennante Nicht-Euklidische Geometrie" (Mathematische Annalen, 4, pp. 573-611), da parte di Felix Klein, che suggerisce anche il nome da allora universalmente affermatosi. [Si tratta naturalmente di un'altra delle figure carismatiche indelebilmente connesse alla storia matematica di Göttingen. Nato a Düsseldorf nel 1849, dopo il dottorato conseguito a Bonn nel 1868, sotto la guida di Julius Plücker, nel 1871 Klein era lecturer a Göttingen (su raccomandazione del suo grande estimatore Alfred Clebsch, che vi insegnava dal 1868). Fu poi professore ad Erlangen (dal 1872), Monaco e Lipsia; tornò a Göttingen nel 1886 (nel 1895 vi fece venire Hilbert da Königsberg), e lì rimase fino alla morte, avvenuta nel 1925.] Si potrebbe dimostrare con numerosi esempi che la nostra critica non è esagerata, qui basterà citare Carl B. Boyer: <<In un certo senso possiamo affermare che la scoperta della geometria non euclidea inferse un colpo mortale alla filosofia kantiana, paragonabile alle conseguenze che la scoperta di grandezze incommensurabili ebbe per il pensiero pitagorico>> (Storia della matematica, I.S.E.D.I., Torino, 1976; Oscar Mondadori, Milano 1980, 1990, pp. 621-622), ed H. Meschkowski: <<l'esistenza della geometria non euclidea rende impossibile all'uomo moderno di restare fermo alla concezione spaziale di Platone e di Kant>> (loc. cit. nella nota 17, p. 87). Vere e proprie "stoltezze" (dietro cui c'è ancora una volta lo "zampino" di Gauss - vedi quanto se ne dice proprio in fine d'appendice - che riteneva la geometria di origine empirica, e voleva verificare con esperimenti ottici se lo "spazio reale" fosse euclideo oppure no), divenute però slogan che continuano a essere ripetuti in ogni dove (cfr. l'introduzione all'appendice), contro le quali lo scrivente ha in progetto un intero libro ("Storia e critica delle cosiddette geometrie non euclidee - Ovvero, molto rumore per nulla, o per poco?", http://www.dipmat.unipg.it/~bartocci/mat/non-eucl.htm), che, quasi completamente terminato "a penna", si spera possa essere elaborato al computer presto.

32 - Qui Hegel entra in chiara polemica con la critica kantiana, offrendone un'interpretazione "pessimista": <<Si ha un enorme svilimento dello spirito, negando ogni valore alla conoscenza>>. Senza voler affrontare una questione di enorme portata, che esula sia dai limiti che ci siamo presentemente proposti, sia dalle nostre capacità di riflessione filosofica, l'introduzione di un altro dualismo sembra poter fornire una soluzione all'ulteriore dilemma. Nell'opportuna distinzione tra spirito e intelletto, si può infatti parlare di una conoscenza che proviene dal secondo e di una conoscenza che proviene dal primo, vedi anche quanto si dice in proposito nella premessa all'articolo "Conoscenza e potenza", pubblicato in questo stesso numero di Episteme.

33 - "La relatività del movimento nell'Antica Grecia", Periodico di Matematiche, 1921.

34 - Paradoxien des Unendlichen, 1851, postumi; ed. it. I paradossi dell'infinito, Feltrinelli, Milano, 1965, p. 69.

35 - "Paleopitagorismo, paradossi di Zenone sul movimento e critica aristotelica", in Scienza, Linguaggio e Metafilosofia - Scritti in memoria di Paolo Filiasi Carcano, Napoli, 1980.

36 - Riteniamo per esempio che all'opinione secondo la quale la conoscenza che si ricava dai giudizi sintetici a priori è più sicura di quella che si deriva dall'esperienza, volesse alludere S. Tommaso asserendo che: <<intellectus est certior quam scientia>> (Summa Theologiae, II Sezione della Parte II, Quaestio VIII, De dono intellectus, Art. 2). Al riguardo vedi anche la nota 42.

37 - Kant - Sechzehn Vorlesungen, gehalten an der Berliner Universität, 1904 (citazione da Piero Martinetti, Lezioni su Kant, svolte presso l'Università di Torino tra il 1924 e il 1927; Ed. Feltrinelli, Milano, 1968, p. 47). Martinetti conferma l'opinione di Simmel, sottolineando che: <<In realtà già Kant aveva preveduto una Scienza di tutte le forme possibili dello spazio e spesso parla di altre forme possibili dell'intuizione. Ciò vuol dire che le intuizioni pure non sono necessità logiche; sono necessarie per la nostra intuizione, ma potrebbero esservene delle altre>>.

38 - Il continuo - Indagini critiche sui fondamenti dell'analisi, 1917 e 1932; ed. it. Bibliopolis, Napoli, 1977, p. 10 - un testo peraltro sostanzialmente illeggibile.

39 - Affermiamo ciò ben sapendo che Weyl viene considerato un caposcuola degli "intuizionisti": un leader invero strano, a giudicare dai suoi entusiasmi relativistici (vedi il paragrafo 8, e la nota 49).

40 - Troviamo che "platonista" faccia inopportuno riferimento a una fase primitiva della riflessione su questi argomenti, mentre a proposito di "kantiano" val la pena riferire un buffo aneddoto. A un laureando che stava cercando di impostare una classificazione delle diverse possibili posizioni filosofiche sulla questione dei fondamenti, e aggiungeva alle solite formalismo, logicismo, intuizionismo, platonismo (che non tutti nominano dopo le prime tre citate) anche il termine kantismo, un componente della commissione d'esame ha chiesto scandalizzato se sapeva citargli un matematico appartenente a tale "corrente", eccettuato naturalmente l'autore del presente articolo, che era relatore della tesi in discussione.

41 - Al tema fu dedicato un apposito convegno nel 1989, a Perugia: "I fondamenti della matematica e della fisica nel XX secolo: la rinuncia all'intuizione" (Proceedings of the Conference on Foundations of Mathematics & Physics, Umberto Bartocci e James Paul Wesley ed., Benjamin Wesley Publ., Blumberg, 1990).

42 - Intelligenza, e quindi intelletto, proviene infatti (a quel che pare: con certe affermazioni bisogna andare cauti) da inter + legere, con l'inter che rafforza l'idea di raccogliere, scegliere, presente in legere (oltre ovviamente al nostro "leggere"), d'onde già in latino il verbo intellegere (o anche intelligere). Un'etimologia più "avventurosa" propone invece intus + legere, cioè leggere, o guardare dentro, che riavvicinerebbe curiosamente il termine all'"intuizione" protagonista di questo articolo, mediante un'altra comune pseudo-etimologia: intuire come intus + ire, ossia andare dentro. Al contrario "intuire" (che i latini rendevano anche con l'espressione animo percipere - assai istruttivo dal nostro punto di vista: sarebbe le coeur di Pascal! - o con il precedente intellegere, il che mostra comunque una connessione almeno semantica, se non strettamente etimologica, tra i vari concetti in discorso), deriva da intueor, intueri, ossia in + tueri, che vale "guardare dentro", ed ecco che in effetti giriamo intorno sostanzialmente alla stessa "idea". Curioso osservare che la detta pseudo-etimologia goda dell'illustre conforto di S. Tommaso: <<nomen intellectus quandam intimam cognitionem importat: dicitur enim intelligere quasi intus legere>> (loc. cit. nella nota 36, ma Art. 1).

43 - Il più comune riferimento alla definizione di S. Tommaso (che concerne la veritas, o veritas logica) rimanda alla Summa Theologiae, I, Quaestio XXI, De Iustitia et Misericordia Dei, Art. 2 (<<veritas consistit in adaequatione intellectus et rei>>), oppure, nella stessa Parte I, alla Quaestio XVI, De Veritate, Art. 2 (<<Isaac [Isaac ben Solomon Israeli (855- 955), medico e filosofo nato in Egitto, di origine ebraica. N.d.A..] dicit, in libro De Definitionibus, quod veritas est adaequatio rei et intellectus>>). La chiara anticipazione kantiana di Cusano, che riguarda la scientia, si trova nel Compendium (10, 34:20-21). Non manca naturalmente chi suggerisce di modificare la definizione proposta dal filosofo di Kues, uno dei "padri della modernità", con: adaequatio intellectus ad rem, trovando l'altra di stampo eccessivamente antropocentrico. Ma è poi possibile, al di là di un certo banale limite, modificare il proprio "sistema operativo"? E' quanto ci si chiedeva, con differenti parole, nel paragrafo 6.

44 - Federigo Enriques chiama in causa per spiegare il medesimo fenomeno la "logica della ragione", nella distinzione che opera tra due tipi di logica: <<Il matematico che nel suo sforzo di astrazione e nel suo desiderio di compiutezza ha purificato la logica discorsiva, si trova condotto a riconoscere che questa logica dell'intelletto postula un giudizio superiore della ragione, che lo porta al di là delle stesse matematiche [...] Distinguere una logica della ragione che supera la semplice logica dell'intelletto non è comune fra i matematici. Il loro amore per ciò che è chiaro e preciso li induce volentieri a concentrare tutta l'attenzione sui criterii meccanici del rigore formale della deduzione o della definizione [...] La discussione sulle definizioni mostra in molti casi quale senso logico più largo venga ad assumere il giudizio razionale>> (Le matematiche nella storia e nella cultura, Lezioni pubblicate a cura di Attilio Frajese, Zanichelli, Bologna, 1938, p. 148). E' chiaro che qui "ragione" ha un'accezione diversa da quella da noi proposta, in cui è sinonimo di "intelletto".

45 - Il termine modello non ci piace troppo, perché ad esso si fa oggi frequente e superficiale ricorso, con lo scopo principale di acquietare senza troppa fatica le coscienze di fronte a problemi epistemologici rilevanti. Per quanto riguarda invece l'attributo "continuo", nell'appendice noi lo riserveremo in effetti a "spazi ordinati", e uno spazio reale pluridimensionale non è ordinato (anzi, non è "ordinabile", cioè non può essere ordinato, almeno in modo compatibile con altre sue strutture naturali che si vogliano conservare, quale quella topologica). Qui "continuo" sta allora per estensione a indicare un oggetto che è costruito sul continuo dei numeri reali, che è sì un "autentico" continuo (in ciascuna delle accezioni che analizzeremo nell'appendice). Val forse la pena di osservare che tutta quest'abbondanza di specificazioni sul "reale" ha invero scarso riferimento alla "realtà", in quanto sia i numeri reali, sia gli spazi su essi costruiti, hanno ben poco a che fare con la res extensa, e sono al contrario enti completamente "ideali". Cioè, che la denominazione "numero reale", con quel che segue, appare "inadeguata", e causa di ulteriori fraintendimenti linguistici del tipo che abbiamo segnalato. Infine, a chiusura di questa lunga nota, specifichiamo che nell'uguaglianza s = t un fisico non vedrebbe assoluta identità, dal momento che i due termini coinvolti avrebbero, come si dice, "dimensioni" diverse, almeno nel sistema di unità di misura oggi comunemente utilizzato (chiamato MKSQ, con riferimento a metro, chilogrammo, secondo e coulomb, l'unità di carica elettrica). Vero, ma si tratta comunque di un primo passo verso un'identificazione che nella teoria della relatività diventa totale, a partire dall'identità s = ct (c la velocità della luce), in cui si ponga c = 1, grandezza scalare "priva di dimensione". In effetti, una distanza (astronomica) si misura ormai in anni (luce)!

46 - Hermann Minkowski, "Space and Time", address at the 80th Assembly of German Natural Scientists and Physicians, Sept. 21, 1908. Con l'espressione <<architetto formalista>> si fa implicito riferimento all'ottimo libro di Lewis Pyenson, The Young Einstein - The advent of relativity (Adam Hilger Ltd, Bristol and Boston, 1985). Dello stesso tema Minkowski si era occupato un anno prima (autunno 1907), rivolgendosi in quell'occasione alla Società Matematica di Goëttingen (solo nel 1915, 6 anni dopo la morte di Minkowski, Arnold Sommerfeld pubblicò il testo di questa conferenza: "Das Relativitätprinzip", Annalen der Physik, vol. 47).

47 - Utilizziamo questi due termini per indicare gli estremi di uno spettro generale di fenomeni nei quali ci si può imbattere in tale campo, senza scendere in analisi dettagliate. Una critica non sempre deve infatti chiamare in causa la disonestà, o non imparzialità, dello sperimentatore (per un altro caso esemplare vedi la nota successiva), ma appunto pure la difettosa interpretazione teorica dell'evidenza sperimentale di cui si vuol tenere conto. In fondo, anche il fatto che il Sole si muovesse in cielo, in un moto da Est verso Ovest, era una delle "evidenze" sotto gli occhi di tutti, prima che la circostanza fosse spiegata attraverso un moto del nostro pianeta intorno ad esso, e non viceversa.

48 - Si veda per esempio "Efficere Deos - A proposito della costruzione del mito Einstein", in:
http://www.dipmat.unipg.it/~bartocci/EFFIC.htm. Vi viene riportato un brillante resoconto di Marco Mamone Capria sul valore (sulla serietà) delle "prove" raccolte in favore della relatività generale dall'ineffabile Sir Arthur Eddington, nel 1919 prima, e nel 1924 dopo. Elemento sicuramente decisivo per l'affermazione non più contrastata della teoria della relatività, e dell'icona Einstein, è la vittoria degli alleati nella II guerra mondiale, con le esplosioni atomiche finali di Hiroshima e Nagasaki, ascritte a "merito" dell'equazione "relativistica" E = mc². E siamo qui di fronte al solito fenomeno di una vulgata (propaganda) frettolosa e superficiale, la quale trascura di sottolineare il "dettaglio" che non c'è alcun bisogno di relatività per introdurre la più celebre equazione della storia della fisica. Senza citare le numerose anticipazioni classiche della formula, pressappoco "esatte" (si veda http://www.dipmat.unipg.it/~bartocci/depre.html, o i punti da C ad H contenuti nella parte finale della pagina http://www.dipmat.unipg.it/~bartocci/listast.htm), ne dà conferma lo stesso Einstein, che, trascorsi parecchi anni dal 1905, anno di pubblicazione della sua breve nota sull'equivalenza massa-energia, presentò una nuova dimostrazione di essa su basi puramente classiche ("Elementary derivation of the equivalence of mass and energy", Bull. Am. Math. Soc., 41, 1935, pp. 223-230) - un afterthought forse riconducibile al tentativo di salvare qualcuna delle "sue" idee, nel timore, al tempo giustificato, che la relatività potesse essere sperimentalmente falsificata? Anche l'illustre fisico italiano Piero Caldirola ammette esplicitamente che: <<L'equivalenza tra massa ed energia può essere assunta anche indipendentemente dai Postulati della Teoria della Relatività>> ("Applicazioni e verifiche sperimentali della relatività ristretta", in Cinquant'anni di Relatività, a cura di Michele Pantaleo, con una prefazione di A. Einstein, Ed. Sansoni, Firenze, 1955, p. 402).

49 - "Truth" ha iniziale maiuscola nella traduzione inglese del testo (Space-Time-Matter, Dover Publications, New York, 1952), chissà quanto concordata con l'autore (scomparso nel 1955). Si potrebbe pensare in effetti a un eccessivo entusiasmo del traduttore, tenuto conto che nella versione originale il corrispondente "Wahrheit" doveva avere necessariamente l'iniziale maiuscola, perché così si usa in tedesco con tutti i sostantivi.

50 - http://www.arrigoamadori.com. Il brano (che tra l'altro non spiega bene perché nello spazio infinito debbano necessariamente esistere infinite stelle e pianeti) fa riferimento al cosiddetto "paradosso di Olbers", che si spiega agevolmente, almeno da un punto di vista qualitativo, con la "teoria dell'etere" (cfr. paragrafo successivo), vedi: http://www.dipmat.unipg.it/~bartocci/olbers.html. Aggiungiamo che certe critiche sarebbero state più apprezzabili ai tempi in cui si levavano al cielo peana in favore della cosmologia di Newton, a detrimento di quella di Cartesio, tanto più che si tratta di osservazioni semplicissime, che non abbisognano di alcun progresso nella conoscenza sperimentale per poter essere formulate. Senza offesa per nessuno, la situazione fa venire alla mente il deprecato Giuseppe Casazza, che in un testo del 1923 così ardiva esprimersi (riportiamo il pezzo per divertimento dei lettori, osservando che, secondo noi, l'autore più di un briciolo di ragione ce l'aveva): <<Agli esami di fisica. - Che cosa è il tempo? - E' lo spazio. - Bene. Ditemi quante sono le dimensioni dello spazio. - Le tre dimensioni dello spazio sono quattro: lunghezza, larghezza, altezza e ... tempo. - Bravo. Sapresti dirmi cosa devesi intendere per velocità infinita? - Per velocità infinita intendesi quella di 300 mila Km al secondo. - Che intendete per secondo? - Per secondo intendo un tempo che risiede nella mente del prof. Einstein, residente a Berlino. - Quindi capirete, neh vero, che anche il valore della velocità della luce, per logica conseguenza, risiede nella mente del non mai abbastanza esaltato prof. Einstein. - Sì. - Bravo, andate al posto, farete carriera>> (Einstein e la commedia della relatività, Milano, 1923, pp. 152-153; citato da Roberto Maiocchi, Einstein in Italia - La scienza e la filosofia italiane di fronte alla teoria della relatività, Ed. Franco Angeli, Milano, 1985, p. 69).

51 - Il principio di complementarità di Niels Bohr, che, per salvare le apparenze, attribuisce a un medesimo ente fisico talvolta caratteristiche di corpuscolo (discreto), talvolta di onda (continuo), è l'ultima spiaggia di un approccio alla filosofia naturale incapace di scorgere le antinomie esistenti nei suoi stessi principi, e cerca di conciliare con un "assurdo" (ne bis in idem) la compresenza di descrizioni continue della realtà (quelle elaborate dalla fisica-matematica post newtoniana, di grande successo al tempo stesso applicativo e ideologico, e pertanto irrinunciabili) e di una sua verosimile struttura fondamentale discreta, cui stiamo qui accennando. Non è difficile aspettarsi poi che "particelle" in movimento nello spazio reale diano origine a un fenomeno nel quale si manifestano entrambe le caratteristiche in esame: la corpuscolarità in quanto alla particella, l'ondulatorietà in relazione all'onda generata nel mezzo dal moto del corpuscolo (come una barca che si muove sulla superficie di un lago, o meglio un sottomarino che naviga nelle profondità del mare). Si veda in proposito anche la nota 6 della "Letter from the Editor to the Readers", nella parte II del numero 6 di Episteme.

52 - Non è questa purtroppo l'opinione di Cartesio, il quale inclina verso una suddivisibilità della materia in infinitum, o quanto meno in indefinitum: <<Così, poiché non sapremmo immaginare un'estensione sì grande da non concepire in pari tempo che può essercene una più grande, diremo che l'estensione delle cose possibili è indefinita. E poiché non si potrebbe dividere un corpo in parti sì piccole, che ognuna di queste parti non possa essere divisa in altre minori, noi penseremo che la quantità può essere divisa in parti, il cui numero è indefinito>> (Principia Philosophiae, Parte I, 26; ribadito nel principio N. 20 della Parte II: <<Che non possono esservi atomi o piccoli corpi indivisibili>>). Qui pare proprio che Cartesio commetta l'errore di confondere il reale con il pensato, e, a parte quello inferiore, ci sarebbe da discutere anche su ciò che riguarda un eventuale limite superiore dei corpi materiali. Si veda per esempio De Pretto (loc. cit.), quando avanza la ragionevole ipotesi che non possano esistere masse maggiori di un certo valore: stelle troppo "grosse" si spezzerebbero, dando origine al fenomeno delle stelle doppie. Insomma, il succo di questo paragrafo 9 è che nella materia propriamente detta non esistono né l'infinitamente grande (questo consisterebbe solo nell'estensione dell'etere-spazio, non della "materia pesante"), né l'infinitamente piccolo: entrambi si danno soltanto nella nostra mente, così che l'uomo sembra davvero potersi proporre come misura di tutte le cose (m e t r o n p a n t w n ), secondo la famosa definizione di Protagora.

53 - In questo scritto (integralmente reperibile in: http://www.dipmat.unipg.it/~bartocci/st/mem-depr-vf.htm) si tenta anche una spiegazione della gravitazione come "pressione" di origine fluido-dinamica (quindi non una proprietà dei corpi, bensì dello spazio materiale che li circonda). Per il "caso De Pretto" in generale, le relazioni di tale studioso con Einstein, e la famosa equazione sull'equivalenza tra massa ed energia, si vedano i punti da C in poi della pagina:
http://www.dipmat.unipg.it/~bartocci/listast.htm.

54 - Si tratta naturalmente di un primo "rozzo" schema per immaginare le proprietà discontinue-discreto-granulari dello spazio fisico reale (i.e., "materia", in due "stati" differenti, di monade d'etere indifferenziata, e di "materia pesante"). Di fronte alla complessità della fenomenologia, nulla esclude la possibilità di introdurre due monadi d'etere distinte ("positiva" e "negativa", "calda" e "fredda", etc.), o una sola monade che sia però "strutturata", come si accenna nell'indefinibile libro di Jean-Luc Chaumeil (Le trésor des Templiers et son royal secret: l'Aether, Guy Trédaniel Éd., Paris, 1994). In esso si descrive una dottrina segreta e tradizionale dello spazio reale, secondo la quale: <<L'Aether occupe et remplit l'univers tout entier. C'est un océan sans limite formé de "petits êtres diaphanes et imponderables" qui pénètrent tous les corps et "ont la forme de petits serpents, tels qu'ils sont représentés sur les abraxas" [...] Tous les phénomènes qui se produisent dans la nature, depuis la formation et la gravitation des astres, jusq'à la création des corps inertes et des êtres animés, sont "l'oeuvre de l'aether">> (p. 292). Citiamo tali parole anche perché l'autore si riferisce a ricerche degli anni '30 (comunicate a varie autorità francesi dell'epoca), e la moderna "teoria delle stringhe" viene costruita solo alla fine degli anni '70. Per non dire della circostanza che l'autore introduce diversi "colori" (blanc, rouge, bleu-noir, jaune), che in numero di quattro formerebbero i "serpentelli", <<chacun des petits serpents [...] est composé de quatre noyaux ou atomes>>, mentre per i sei tipi di quark (in realtà, tre quark e tre anti-quark), ipotizzati nel 1963 dai fisici americani Murray Gell-Mann, premio Nobel 1969, e George Zweig) si parla esplicitamente di "colore" (una nozione presentata da O.W. Greenberg, M.Y. Han, Yoichiro Nambu nel 1965; ma i colori dei quark sono solamente tre, e precisamente rosso, verde e blu).

55 - Un complesso di teorie che, data la scomparsa dell'etere decretata da Einstein nel 1905 (salvo a successivamente "pentirsi", e ritrattare in parte: cfr. la recensione a Ludwik Kostro, Einstein and the ether, Apeiron, Montreal, 2000, in Episteme N. 3), sono state costrette a fare ricorso alle famose interpretazioni "irrazionali" (vedi nota 25), analizzate secondo il "giusto" punto di vista nell'ottimo: Franco Selleri, La causalità impossibile - L’interpretazione realistica della fisica dei quanti (Ed. Jaca Book, Milano, 1987). Si può aggiungere che qualche "frammento" delle presumibili proprietà dell'etere viene talora reintrodotto, seppure in sordina.

56 - Il valore indicato può apparire strabiliante, ma così non è, come mostra il seguente esempio. Data la semplice equazione algebrica in due incognite (del tipo cosiddetto di Pell): x²-991y² = 1, della quale si cercano soluzioni intere positive, si sa che la più piccola soluzione possibile (in effetti ce ne sono infinite) comporta ben 30 cifre decimali. Si pensi di volerla determinare con l'ausilio di un computer, cominciando a porre y = 1, y = 2, etc., e chiedendo alla macchina di valutare se l'espressione 1+991y² è oppure no un quadrato perfetto. Dopo quanto tempo il computer ci risponderebbe affermativamente? Facciamo qualche calcolo. Il numero dei secondi trascorsi dal big-bang fino a oggi (peraltro un evento "mitico" della cui "realtà" vari articoli pubblicati su Episteme hanno dubitato), considerandolo avvenuto 15, 17, o perfino 20 miliardi di anni fa, sono dell'ordine di 10¹⁸ (infatti, in un minuto ci sono 60 sec, in un'ora 60 minuti = 3600 sec, in un giorno 24 ore = 24* 3600 = 86.400 sec, in un anno circa 365* 86.400 = 31.536.000 sec, una quantità non superiore a 4* 10⁷ sec, e in 20 miliardi di anni, ossia 2* 10¹⁰ anni, ci sono non più di 8* 10¹⁷ sec, vale a dire non più di 10¹⁸ sec, approssimando sempre largamente per eccesso). Allora, se ogni verifica venisse effettuata anche solo in un decimiliardesimo di secondo, cioe' 10^-10 secondi, per arrivare a 10³⁰ ci vorrebbero comunque 10²⁰ secondi, e quindi parecchi miliardi di anni, cento volte più che tutto il tempo passato dalla pretesa origine dell'universo a oggi. Eppure, la mente dell'uomo è riuscita a trovare il risultato esatto in molto meno.

57 - Questa è esattamente la fisica unifenomenica cartesiana (di cui all'articolo di Rocco Vittorio Macrì citato alla fine del paragrafo 7): tutta la molteplicità del reale non è altro che apparenza di diversi movimenti dell'etere, come descritto nel voluminoso La teoria delle apparenze di Marco Todeschini (vedi: http://www.dipmat.unipg.it/~bartocci/todes.html). Un'interessante ripresa di siffatti motivi (che, nonostante le forze contrarie, si ripresentano e si ripresenteranno inevitabilmente, generazione dopo generazione) è offerta da Fred Evert, nel suo sito http://www.evert.de/eft00e.htm. Tale autore afferma esplicitamente: <<There are no solid bodies wandering through universe - only their motion-pattern of ether are moving through ether>>.

58 - Se si desidera pagare qualche tributo agli idola del pensiero scientifico del XX secolo, si può fare menzione in tale contesto al principio di indeterminazione di Heisenberg, ma è chiaro che secondo noi non si tratta altro che dell'inconciliabile contrasto tra il continuo e il discreto nella nostra mente, quando viene chiamata a percepire qualsiasi tipo di "dinamica".

59 - E' chiaro che optare per la seconda alternativa implica un'ulteriore denigrazione anti-antropocentrica dell'"umano", attraverso una riduzione della sua componente "divina". Si rammenti anche l'osservazione di Spinoza riportata nel precedente paragrafo 9.

60 - Dovrebbero essere ormai palesi le motivazioni alla base della mancata indicazione di un "tempo reale". Il tempo appartiene esclusivamente al dominio della coscienza, e non della res extensa, cui è proprio solo il cambiamento. Si può parlare comunque di un tempo fisico misurato (vedi peraltro la nota 29, e quanto se ne dice nel paragrafo 9: un punto di vista appena abbozzato, che si potrebbe convenientemente approfondire), ed esso sarebbe presumibilmente ancora discreto.
 
 

Un ringraziamento speciale deve essere rivolto alla Dott.ssa Annarita Pietrantozzi, che si laureò in matematica presso l'Università degli Studi di Perugia nell'A.A. 1982-83, con un'ottima tesi dal titolo "Il ruolo dei paradossi di Zenone nel problema dei fondamenti della matematica" (qui ampiamente utilizzata), e che da allora lo scrivente, il quale fu relatore della tesi in parola, ha purtroppo perduto di vista, rimandando il momento della definitiva elaborazione di certi concetti per oltre vent'anni.
 

[Una presentazione dell'autore si trova nel numero 1 di Episteme.]

bartocci@dipmat.unipg.it
 

La spiegazione offerta da Cartesio per il paradosso dell'Achille si trova in una lettera indirizzata al cognato Claude Clerselier, che fu il primo curatore del relativo epistolario tra il 1657 e il 1667 - di lui si dice che, fervente cattolico, <<began the process of turning Descartes into a saint by cutting, adding to, and selectively publishing his letters. This cosmetic work culminated in 1691 in the massive biography by Father Adrien Baillet, who had previously published a 17-volume Lives of the Saints. Even while Descartes was still alive, there were questions as to whether he was a Roman Catholic apologist, primarily concerned with supporting Christian doctrine, or an atheist, concerned only with protecting himself with pious sentiments...>> (http://www.hfac.uh.edu/gbrown/philosophers/leibniz/BritannicaPages/Descartes/Descartes.html).
Nell'edizione da cui l'abbiamo tratta (Lettres de M^r Descartes, Paris, Chez Henry Le Gras, 1657, pp. 655 e segg.), essa appare priva della data, ma va certamente collocata in un periodo di poco anteriore al viaggio in Svezia (ottobre 1649) che avrebbe dovuto condurre il grande filosofo alla morte nell'anno successivo. Poiché non l'abbiamo vista citata in nessun sito Internet, pensiamo di fare cosa utile presentando ai lettori una sua pagina (la lettera è reperibile presso la sezione elettronica della Bibliothèque nationale de France, http://gallica.bnf.fr/).
 
 

Key words: Zeno, Zeno's paradoxes, Space and time, Duality, Descartes, Lettre à Clerselier, Continuous, Discrete