
Concezione meccanica dell'elettromagnetismo secondo Maxwell
ELECTROMAGNETISM IN THE ETHER
(Giuseppe Cannata)
To attribute an inertia to free space is not an option. It is soundly consistent with the fundamental laws of physics. The mechanical interpretation of electromagnetic phenomena would supply a concrete way of simplicity and unification. Consequently, the revised quantum theory could become without any contrast a modern chapter of a renewed classical physics. Here it is proposed a new elementary charge model, which would simplify the interpretation of many phenomena, including the controlled nuclear fusion.
1 - Introduction
In the study of mechanics it is better to go from kinematics to dynamics by introducing an essential property of the body: mass or inertia. Momentum, force and energy ot the body have dimensions which contain always mass. The equations in which mass does not appear are merely kinematic. Linear and angular momenta, force and energy, in electromagnetism. do not explicitly contain mass. Nevertheless, by not wanting to consider them distinct quantities from those introduced in mechanics, and used in other sections of physics, they clearly must contain inertia, even when referring to vacuum localizations. We must therefore admit that vacuum has mass and may be easily called ether again.
Of course, the global and specific characteristics of the ether must be made clear, by eliminating some wrong interpretations of the past.
2- Global characteristics of the ether
a) It is no-sense to consider ether being absolute, since up to now none has been able to carry out observations of its stationarity in any part of the Universe.
b) Partial or total drag of the ether does not exist. Ether is an integral part inside and around a star or a particle, and extends itself with decreasing density up to a limit surface, beyond which it belongs to another star or particle. Our planet, for example, as an ether-terraqueous system is not spheroid-shaped like the terraqueous nucleus, but it is like a huge drop, which is compressed on one side by solar wind, while in the opposite side it is extended with a long geomagnetic tail. Michelson and Morley experiment does confirm the relative rest of the ether in the Earth's proximity, as the interferometer does not reveal a significant fringe shift. Bradley's stellar aberration has up to now been interpreted as an experience consistent only with an absolute ether. The astronomical telescope, pointed to the zenith toward the nearest star, must be inclined, with respect to the vertical line, of an angle a , according to Earth's movement. This angle is such that: tg a = u/c , where u is Earth's orbital speed and c light's speed. But the light coming from the star takes years to reach the Earth, that is to say, it travels only a few terrestrial diameters in which the ether belongs to the Earth, a distance which will always be negligible in respect to the star-Earth distance. Thus, the phenomenon can still be interpreted in Bradley's way, the thick layer of terrestrial ether notwithstanding.
c) Ether is not continuous. The granularity or quantization of mass and energy is a universal characteristic. lt is evident that in acoustic phenomena the quantum of mass is a molecule of the substance which constitutes the medium of propagation. Ether can be conceived as composed by extremely small particles (ether monads), each one "insignificant", such perhaps as neutrinos, gravitons etc., however quanta of various kinds of aggregation. The organized collectivity of these entities is what we observe. The actual knowledge goes from the neutrino to the galactic clusters. In this huge range each system appears to be formed by subsystems, and so on. Each particle has a complex structure, determined by laws which are not always known, but which we often describe as more complicated than they truly are.
d) Last century, light waves transversality made physicists assume an ether paradoxically gelatinous. In Maxwell synthesis, electric and magnetic fields are functions of transverse waves to be compared with shearing stress, existing only in solid bodies. Intrinsic rotationality of both fields makes the resort to the paradox useless.
e) However, ether is able to transmit all perturbations from the electromagnetic to the nuclear, to the gravitational, without even excluding pressure and temperature ones. It would be enough to consider that volume variations require a variation of intermolecular spaces, and that temperature varies with e.m. radiations through the interposed ether.
3 - Quantitative properties of the ether
Wave phenomena are based on contiguity of particles constituting the medium, for instance molecules in the air, and not on continuity. Continuity is adopted in physics only in the macroscopic vision of microphenomena, supported by the powerful differential calculus.
We know that the speed c of e.m. waves in vacuo is:
(3.1) c = 1/![]() (e
0m
0)
(e
0m
0)
where e 0 = 8.85*10-12 farad/m is the permittivity of vacuum and
m 0 = 4p *10-7 henry/m is the permeability of vacuum.
If we compare (3.1) with the speed v of acoustic waves:
(3.2) v = ![]() (k/r
)
(k/r
)
where r is the mean density of the medium at rest, and k is its compression module, then e 0 can be interpreted as a mean density of the ether in rarefied air (in I.S. measures: Kg/m3).
We may obtain the same result by Coulomb's force:
(3.3) F = qq'/4p e 0r2
between point charges q and q' at a distance r. As a matter of fact:
1) The force at the right-hand side of (3.3) has a physical dimension which contains mass, and this has to appear in the left-hand side too.
2) As charges without mass have never been observed, it is reasonable to think to a mass square in the right-hand side of (3.3), wich should appear in the product of the two charges; consequently, one should think to the presence of mass in the constant e 0 .
Remark 1 - Incidentally, we notice that the numerical value of e 0 , or possibly an even smaller value in the interplanetary and interstellar spaces, would support the astrophysicists view in the search of a dark matter (or missing mass) to close up the Universe. Furthermore, the red-shift of spectral lines of stars, interpreted until now as a Doppler effect due to the recession of galaxies, of magnitude related to the distance of the star (cosmic expansion), would be caused instead by the attenuation of the energy as the light travels through space, and would then increase with the increase of distance. In this way the hypotheses of big-bang, black holes, etc. would not stand any more. Ether inertia would also explain the gravitational cohesion of many galaxies, which is another astrophysics puzzle.
Going back to (3.1), considering e 0 as a density, we have:
(3.4) 1/m 0 = 7.96*105 N/m2
which is a value comparable to air's compression module:
(3.4) k = (cp/cv)p0 = 1.4*105 N/m2
(cp and cv are molar heat capacities of biatomic gases, respectively at constant pressure and constant volume, and p0 is the standard pressure of the atmosphere).
4 - Origin of the electromagnetic field
From (3.3) the dimensions of a mass flow for the electric charge can be deduced as:
(4.1) q = dm/dt ( [q] = MT-1 ) .
Proton p and electron e are like ether line vortices, which in Helmholtz fluid dynamics maintain mass flow (l.6*10-19 Kg/s) and angular momentum. Two model symbols of p and e, and of the neutron, can be seen in the previous article written in Italian. The proton consists in a tiny axial permanent jet of ether at a conservative velocity Er ("old" central electric field) with compensating vortex flows ("old" induced electric field Ei). On the contrary, electron aspirates ether axially, and spreads it out by circular swirls. The recovery of the ether is accomplished by the contiguity of similar ether vortices.
The electric field has, in this way, kinematic dimensions of a local velocity of ether: E=LT-1 , which experimentally does not exceed 3*106 m/s ("old" dielectric strength in V/m) in the air, and about 2*108 m/s in mica, values which are however not exceeding light's speed c = 3*108 m/s.
A distribution of elementary charges on the surface of a conductor, in equilibrium, produces externally a conservative velocity field Er . While the field Ei produces the attraction of similar parallel charges, according to Bernoulli's theorem on fluid dynamics, and cancels the induction field B , which has opposite values between equally directed charges.
Thinking of a charge distribution on the two opposite sheets of a parallel-plate capacitor, the number of field lines is finite and equal to the number of elementary generating charges. Indeed, if paradoxically two or more field lines would come out from a same single proton inclosed in a conducting shell, they would attract on the internal surface just as many electrons, and this would call on the outer surface of the shell just as many positive ions, clearly in excess of the inducing charge. And this would be in contrast with experiments and with Gauss theorem. Thus, an elementary charge acts directly only on a single opposite charge, as it happens naturally in neutral atoms. The model of point charge in spherical distribution can be applied only on a large scale.
Remark 2 - According to this new scheme, the elementary electric dipole differs substantially from the presently known one, which is formed by two small spheres wich opposite charges.
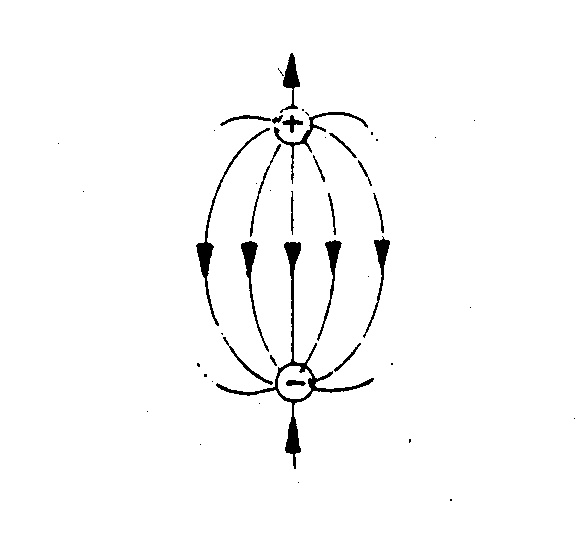
Today's model of dipole
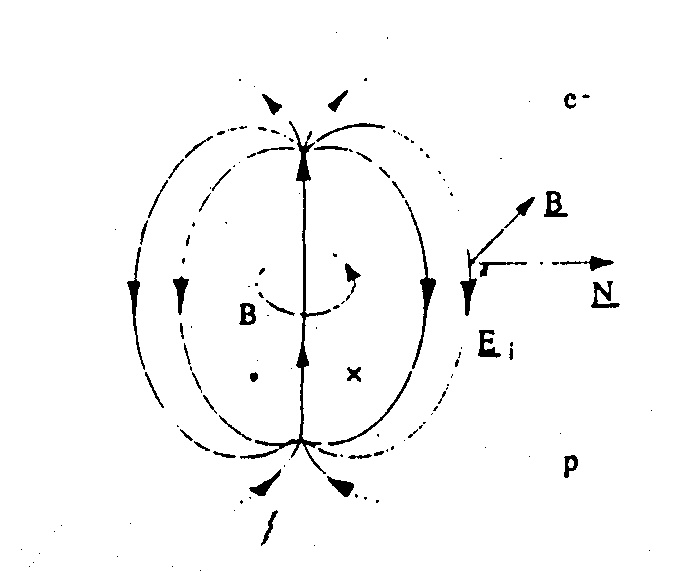
New proposed model of dipole
The two schemes agree only in the straight line going between the two opposite charges. In the old model, the other lines are all radial, irrotational, conventionally coming out from the positive charge. In the new proposed model, the same lines are rotational, opposite to the central field (straight line) and generating, in turn, a rotational magnetic field. An electric dipole, perturbed by either collisions of particles or by the incidence of e.m. radiations, does radiate in turn e.m. waves. Traditional dipole and much less accelerating charges do not clearly explain this e.m. waves generation. Furthermore, a central field has never been indeed observed in the surrounding space. Our model shows instead that the central field exists only in the antenna circuit. Besides, it locates the electric and magnetic fields, perpendicular and in time phase between themselves, and both transverse to the direction of propagation. In addition, the old model does not explain why the dipole cannot irradiate along its axis. By observing the new scheme one can obtain answers in agreement with all experience.
5 - Mechanical interpretation of Maxwell equations
From a macroscopic Laplacian point of view, any point (elementary volume) of a fluid is located by a position vector, whose origin is in the center of a coordinate system, fixed in an inertial reference frame. We denote this vectorial function by A(x,y,z,t).
Any elementary displacement:
(5.1) dA = Ñ (dy ) + dq Ù A
is the vector sum of two components:
1) Ñ (dy ) is the radial component, when the position vector A changes only in absolute value (y is a potential surface scalar function);
2) dq Ù A is the rotational component, when A changes only in direction.
The (opposite of the) time rate change of A is given by:
(5.2) E = -¶ A/¶ t = -Ñ (¶ y /¶ t) - w Ù A
where E is a local velocity field. The first term in the right-hand side of (5.2) gives the radial component of the field, while the second term is its rotational component. ¶ y /¶ t = j is the velocity potential function; w the angular frequency. The minus sign indicates that the terms of (5.2) are reactive and correlated to the principle of energy conservation. (5.2) expresses the Cauchy-Helmholtz theorem on the velocities in fluids.
We can write it again as:
(5.3) E = -Ñ (j ) - ¶ Ai/¶ t
where ¶ Ai/¶ t = rotational displacement.
Two Maxwell equations can be now immediately deduced:
I) by applying curl operator to both sides of (5.2):
(5.4) curl(E) = -¶ curl(A)/¶ t = -¶ B/¶ t
[where, as usual, B = curl(A) ; of course, when one decomposes E in the two components Er and Ei , respectively radial and rotational, since the first component Er is conservative, then one has:
curl(E) = curl(Ei) = -curl(¶ Ai/¶ t) , in force of (5.3) - the equation (5.4) is obviously concerning e.m. induction phenomena].
II) by applying div operator to B = curl(A) :
(5.5) div(B) = 0 ,
which states that B is a solenoidal field.
In Maxwell theory A is obviously the magnetic vector potential, B is the magnetic induction vector, j is the electric potential.
The charge density s (x,y,z,t) in coulomb/m3 can be interpreted in this model as:
(5.6) s (x,y,z,t) = ¶ e (x,y,z,t)/¶ t [ s has physical dimension L-3MT-1 ]
We notice that the mass density e (x,y,z,t) of the ether is surely variable where an electric charge is localized.
The second law of dynamics applied to a unit volume of a fluid, whose density is r and whose velocity is v , and consequently its momentum density is r v , can be written as:
(5.7) Fu = ¶ (r v)/¶ t = r ¶ v/¶ t + v¶ r /¶ t .
In the same way as the time derivative of momentum density e E is proportional, according to Hooke's law, to curl(B) , the module of elasticity 1/m 0 can be written as:
(5.8) ¶ (e E)/¶ t = e ¶ E/¶ t + E¶ e /¶ t = (1/m 0)curl(B) .
The term e ¶ E/¶ t does refer to the boundary of the unit volume where e does not vary (as e 0 in vacuo), and so we can write it as e 0¶ E/¶ t . In the term E¶ e /¶ t the unit volume is supposed instead to contain charges.
Introducing (5.6) into (5.8) gives:
(5.9) curl(B) = m 0e 0¶ E/¶ t + m 0s E = m 0(e 0¶ E/¶ t + j)
which does coincide with another Maxwell equation (one defines:
j = s E the vector field density current).
By applying div operator to both member of (5.9), we get:
(5.10) div(j) = -¶ (div(e 0E))/¶ t ,
and, if we put:
(5.11) div(e 0E) = s = ¶ e /¶ t ,
we obtain at last:
(5.12) div(j) = -¶ s /¶ t .
(5.11) and (5.12) are both continuity equations, and express respectively mass conservation and consequently charge conservation. (5.11) is Maxwell's fourth equation, local expression of Gauss theorem.
6 - The magnetic field
The magnetic field vector H has the dimension L-1MT-2 of a volume vortex torque. The magnetic induction B is dimensionless as an angle. Hence the expression of energy density:
(6.1) w = ![]() H.dB = m
0H2/2
H.dB = m
0H2/2
is similar to the rotational energy:
(6.2) W = ![]() t
.dq
,
t
.dq
,
where t = torque; dq = rotation infinitesimal angle.
We can also mention that (6.1) is the energy density which is dissipated in an hysteresis loop by a ferromagnetic substance.
We have already asserted that the parallel elementary charges give rise to a magnetic field. The field B of each charge has concentric circular flow lines on planes, which are perpendicular to the rotation axis, the latter representing the direction of the central field Er (see previous pictures of the proposed vortex models for proton, electron, and neutron). The neutron, as a close coupling between proton and electron, instable outside the nucleus, has the same field B of proton and electron. In the same way, the atom of hydrogen is a steadier loose coupling of proton with electron. The molecule H2 of the hydrogen is the parallel coupling of two atoms with double field B. All these particles behave as diamagnetic elements, opposing their magnetic field to an external one. The particle rotation is such that as to inclose an area from where its field B is going out. The stationary particles present a spin instead of an orbital angular momentum. All this is in accordance with Faraday's law and Lorentz force.
It should be noticed that the new interpretation attributes to these particles only an induced, and not a pre-existing, magnetic momentum. Furthermore it points out the presence of a magnetic reaction also in neutral particles, as it has been experimentally confirmed. As a matter of fact, in our mechanical model even elementary charges have a spin, and for instance Stern-Gerlach experiment on the splitting of a narrow beam of atoms (for instance of Ag or H2), submitted to a non uniform but symmetric magnetic field, can been easily explained under our hypotheses - without introducing at all a presumed directional quantization of a magnetic dipole momentum, which in our opinion does not exist.
7 - Energy of electromagnetic waves
Let's examine plane monochromatic linearly polarized e.m. waves. We first remark that energy densities of E and B are identical:
(7.1) w = e 0E02/2 = B02/2m 0
(E0 is the amplitude of the electric field, and B0 the amplitude of the induction field).
The same identity is found for acoustic waves:
(7.2) w = r w 2s02/2 = p02/2r v2
where r is the density of the medium, w the angular frequency, v the propagation velocity, s0 the amplitude of displacement, p0 the amplitude of pressure variation. We will come back again to this in the following.
We can now get the equation which rules e.m. waves propagation - in a chargeless and therefore currentless space, that is to say outside of conductors (Ñ (j ) = 0). Keeping in mind that in this case equation (5.11) yields curl(B) = e 0m 0¶ E/¶ t , and that B = curl(A) , E = -¶ A/¶ t, we obtain, by means of simple substitutions in the first previous equation:
(7.3) e 0m 0¶ E/¶ t = curl(curl(A)) = e 0m 0¶ 2A/¶ t2 = Ñ 2(A) - Ñ (div(A)) .
We introduce now the well known "gauge condition":
(7.4) div(A) = 0 ,
and we get at last from (7.3) the wave equation:
(7.5) Ñ 2(A) - e 0m 0¶ 2A/¶ t2 = 0 .
The magnetic potential vector A, which is today usually introduced as a not univocally defined mathematical function, without any physical meaning, is now interpreted as an ether displacement, namely as a primary wave function, an observable physical quantity, from which all the others electromagnetic quantities can be deduced.
Remark 3 - As far as (7.4) is concerning, a divergence different from zero of a vector function would paradoxically contrast the homogeneity of free space! The other commonly used (for instance by Landau) Lorentz gauge condition:
(7.6) div(A) = - e 0m 0¶ j /¶ t ,
which is invariant from the relativistic point of view, is not physically meaningful, since potential j is not a spatial wave function. The variable potential electric field only exists between two opposite distributions of charges in conductors, or between the plates of a capacitor. No experiment has, up to now, located in free space any electric field, variable and conservative, acting in the direction of propagation, that is to say, a longitudinal electric field! Even this persisting confusion can be overcome by the mechanicai tnterpretation of electromagnetism, according to the presently proposed model of elementary charge. Of course, when the function j is a constant in the time, then the equation (7.6) coincides with (7.4).
Coming back to our point, chosen the positive axis x as the propagation direction, and the plane xy as polarization plane, a displacement wave function solution of (7.5), which has now the following form:
(7.7) ¶ 2Ay/¶ x2 - e 0m 0¶ 2Ay/¶ t2 = 0 ,
is a function of the kind:
(7.8) Ay = A0sin(kx-w t)
where k = 2p /l is the wave number, l the wave length, and w = 2p n the angular frequency, l n = propagation speed = c , c2 = 1/e 0m 0 (see (3.1)).
The local velocity field is obtained by derivation of (7.8):
(7.9) Ey = -¶ Ay/¶ t = w A0cos(kx-w t) = E0cos(kx-w t)
while the rotational relative stress is:
(7.10) Bz = -¶ Ay/¶ x = kA0cos(kx-w t) = B0cos(kx-w t)
Taking into account (7.9) and (7.10), we obtain in fact the same energy densities, according to (7.1):
(7.11) e 0E02/2 = e 0w 2A02/2 = 2e 0p 2n 2A02
and
(7.12) B02/2m 0 = k2A02/2m 0 = 2p 2A02/l 2m 0 = 2p 2A02/(1/e 0n 2) .
- - - - -
e-mail: giorgiocannata@inwind.it