Abstract

The maximum of the entropy due to irreversibility has recently been demonstrated as a principle of stability for the open systems. This principle is applied to biological systems to obtain their thermodynamic conditions of stability. A thermodynamic analysis of the synthesis of the ATP is developed.

Keywords: bio-chemical reactions, Irreversible entropy, Maximum entropy, synthesis of ATP, thermodynamic biological systems, thermodynamic stability of biological systems

Nomenclature

Latin symbols

b constant

E Ecological function [J/s]

g molar Gibbs energy [J/mol]

J generalised fluxes

L interference coefficients [K s/kg²]

L_T Thermodynamical Lagrangian [J]

L Lagrangian [J/(m³K s)]

P power output [J/s]

R ideal gas constant (= 8.314 [J/(mol K)])

S entropy [J/K]

t time [s]

T temperature [K]

V Volume [m³]

Greek symbols

C scalar value of generalized forces

h efficiency

u reaction velocity [mol/(m³s)]

x generalised lagrangian thermodynamical coordinates

Y non-linear dissipative potential [J/(kg s K)]

Subscripts

env environment

int internal

irr irreversible

sys system

Symbols

d differential variation

D finite variation

ADP adenosine diphosphate

ATP adenosine triphosohate

C carbon

CO₂ carbon dioxide

H₂O water

O oxigen

P phosphorus
 
 

I. - Introduction

Energy conversion processes are relevant in the biological systems and, as a consequences, they have been studied in the thermodynamic analysis of the living systems [1-3]. The study of linear energy converters working in steady states has been also developed in linear irreversible thermodynamics and the concept of efficiency has been first introduced [1,2]. Moreover some biological systems have been analysed as optimum working regime [2] and in relation to dissipations [4].

Recently some optimisation criteria have been analysed for biological systems by means of the irreversible thermodynamics [2]. The results obtained is that "the election of the working regime depends on the needs or evolutionary advantages it provides, which could differ among species" [2].

In thermodynamics of the irreversible processes a general principle of stability, the maximum variation of the entropy due to irreversibility, for the steady states of the open systems is deduced by means of the calculus of variations [5,6]. Then this principle has been shown to be the general evolution principle of the natural systems [7-11].

In this paper the irreversible entropy maximum principle will be applied in the analysis of the thermodynamic biochemical engineering systems evaluating their efficiency.

II. - Maximum principle for the open systems

To obtain the maximum principle for the open systems, a global analysis was developed [5,6]. The initial and the final states are assumed uniquely defined and stable, and the system has a response time t after which it goes from the initial to the final state. Thus the state functions satisfy the conditions of the calculus of variations [5-8].

Following Gyarmati [5,6,8,9] a continuum general system was examined and its partition in its subsystems with mass dm and volume dV = dm/r , with r the density, has been made.

For every sub-system the density of the thermodynamic Lagrangian per unit of time and temperature L been defined as:
 

(1)                                                L =
 

where L_T is the thermodynamic Lagrangian. The analytical expression of L is [5,6,8,9]:
 

(2)                                                L = 
 
 
 

where [5,6,8]:
 

(3)                                         
 

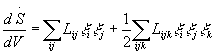
with x generalised co-ordinates, and Y, the non-linear dissipative potential density, is [5,6]:
 

(4)                                         
 

To obtain the thermodynamic Lagrangian from the relation (1) the integration on the total volume V, on the temperature and on time was done, obtaining by the analytical expression (2), with the (3) and (4), and by the Gouy-Stodola theorem, which states that when a system operates irreversibly it destroys work at the rate that is proportional to the system's rate entropy generation [6], the following expression [5-9]:
 

(5)            L = 
 

where DSis the variation of the entropy due to irreversibility.

Thus, as a consequence of the principle of the least action [5-7], the following result was obtained [5-8]:
 

(6)                                                            d(DS_irr) = 0
 

So the required principle of stability for the open systems stationary states was deduced and demonstrated. This principle can be expressed as: "the condition of stability for the open systems' stationary states consists of the maximum for the variation in the entropy due to irreversibility" [6-9].

This principle, here shown in its most general form, has been verified both in linear and in non-linear physics [5-9,11].

III. - Entropy due to irreversibility in biological systems

In irreversible thermodynamics the steady states revel themselves very interesting because they are characterised by the constancy in time of their thermodynamic variables, even when they are not homogeneous inside the system's bulk; to maintain these inhomogeneities there are required some fluxes like mass, energy or others [2,5-8,11-20].

Now a steady state system, characterised by two coupled processes with generalised fluxes (,) and corresponding forces (X₁,X₂) considered. Considering the near-equilibrium irreversible thermodynamics, the time variation of the internal entropy of the system is defined as follows [2,5-8,11-13,16,18-20]:
 

(7)                                                         = J₁X₁+ J₂X₂
 

Following Santillán et al. [2] only internal irreversibility are considered because it has been shown that they are the only responsible of the whole entropy increments of the universe [1,2,5,7-9,18-21].

The total entropy increments are the results of the internal and external contributions of the entropy variations both of the system and of the environment :
 

(8)                                                     
 

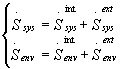
It has been shown [2] that
 

(9)                                                     
 

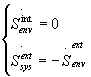
so that the relations (8) becomes:
 

(10)                                                     
 

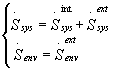
As a consequence the total entropy increments in time, due to irreversibility, , is:
 

(11)                                     = + = = J₁X₁+ J₂X₂
 
 
 

where, the in many biological systems, Xis considered constant [1,2].

Recently has been first introduced the ecological function E:
 

(12)                                                           E = P - T
 

where P = - T J₁X₁ is the power output and T is the equilibrium temperature. The ecological function must be maximised in the steady state [21].

Considering the relation (11) in the relation (12) it follows:
 

(13)                                                        E = - T (2 J₁X₁ +J₂X₂)
 

Using the maximum irreversible entropy variation coupled with the condition of maximum for the ecological function, the following relation can be deduced:
 

(14)                                      
 

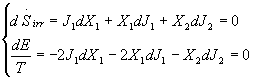
Solving this system and considering that   J= , with i = 1,2 and L Onsager coefficients [2,5-8,12-16,18], such that L= L, it follows that the condition of stability of the steady state for biological systems is:
 

(15)                                                     
 

IV. - Application to thermodynamic biochemical engineering systems: the synthesis of the ATP

In order to employ the previous results in the thermodynamic analysis of the biochemical engineering systems, the hypotheses of the linear irreversible thermodynamics model, here deduced, are summarised in the following:

i) the biological system is in a non-equilibrium steady state consisting of two coupled process

ii) the driven force  X₂  must be constant

iii) only linear relations are considered.

It has been demonstrated that these hypotheses are acceptable for many biological systems [1,2].

Following Sántillan et al. [2] the synthesis of the ATP is considered in anaerobic glycolysis and in respiration. The chemical energy conversion can be described by the following chemical equations, in which the driver reaction is indicated with curly brackets and the driven reaction by square brackets:
 

(16)                        {glucose} + [2 ADP + 2 P⁺] / {2 lactate} + [ 2 ATP]

               {6 O₂+ glucose} + [36 ADP + 36 P⁺] / {6 CO₂+ 6 H₂0} + [36 ATP]
 

For this system the generalised fluxes and forces are [2]:
 

(17)                                                             
 

where uand uare the reaction velocities, such that u= u= u [2], while Dg₁ and Dg₂ the molar Gibbs energies changes of the corresponding reactions.

For this reaction the linear phenomenological Onsager coefficients are [2]:
 

(18)                                 L₁₁ =  L₂₂ = L₁₂ =  L₂₁ = 
 

where uis the maximum forward velocity, b a positive constant that takes into account the enzymatic processes and R the ideal gas constant [2].

Introducing the definition of efficiency h = - ( J₁X₁ +J₂X₂)  [1,2] and considering the relations (17), (18) and (15) the following result can be obtained:
 

(19)                                                    h = 
 

Using the data present in literature [2,21] about the chemical reactions (16) the numerical evaluation of (19) for the chemical reactions (16) is the following:
 

(20)                                                                 
 

according to the measured values presented in the Reference [2].

V. - Conclusions

The principle of maximum for the variation of the entropy due to irreversibility has been summarised. It follows that it represents a general principle of investigation for the stability of the open systems. In fact this principle states that: "in a general thermodynamic transformation, the condition of the stability for the open systems' equilibrium states consists of the maximum for the variation of the entropy due to the irreversibility".

This statement represents an important result in Irreversible processes Thermodynamics because it represents a global theoretical principle for the analysis of the stability of the open systems' states.

The result here obtained must be compared with the ones recently obtained by Bejan [11]. In fact, Bejan has developed the "constructal" theory, a theory by which it is possible to predict some macroscopic shapes, originated by the spatial organisation, in Nature, both in living and in non-living. The Bejan result is an optimisation principle. Bejan himself has pointed out that the theoretical bases of the architecture of many living and non-living systems remains an unknown design principle [11].

The irreversible entropy maximum principle [6] represents the theoretical fundamental of this design principle.

Starting from this thermodynamic result the biological systems have been analysed by the irreversible entropy maximum principle and a condition for the stability of their steady states has been obtained.

A particular application has been done to the synthesis of the ATP: the results obtained agree with the measured ones present in literatures.
 
 

[1] S.R. Caplan and A. Essig, Bioenergetics and Linear Nonequilibium Thermodynamics, Harvard University Press, Cambridge, 1983

[2] M. Santillán, L.A. Arias-Hernandez and F. Angulo-Brown, Some optimisation criteria for biological systems in linear irreversible thermodynamics, Il Nuovo Cimento, D19, 1 (1997) 99

[3] G.P. Johari and G. Salvetti, On the temperature-invariant enthalpy change and thermodynamics of protein's transformation, Il Nuovo Cimento, 19D, 5 (1997) 753

[4] M. Fabrizio, The concept of dissipation in complex systems, Ricerche di Matematica, XLI, Supplemento (1992) 123-132

[5] U. Lucia, Analisi Termodinamica della cavitazione con transizione di fase, PhD Thesis, Università di Firenze, 1995 (in Italian)

[6] U. Lucia, Mathematical consequences of the Gyarmati's principle in Rational Thermodynamics, Il Nuovo Cimento, B20, 10 (1995) 1227

[7] U. Lucia and G. Grazzini, Global analysis of dissipations due to irreversibility, Rev. Gén. Therm., 36 (1997) 605

[8] U. Lucia, Maximum principle and open systems including two phase-flows, Rev. Gén. Therm.,37 (1998) 813-817

[9] U. Lucia, Irreversibility and entropy in Rational Thermodynamics, Ricerche di Matematica, in printing

[10] U. Lucia, Geometrical characteristic and heat transfer in building's protruding structure, Il Nuovo Cimento, D18 (1996) 41

[11] A. Bejan, Contructal theory: from thermodynamic and geometric optimisation to predicting organisation in Nature, Flowers'97, Florence World Energy Research Symposium "Clean Energy for the New Century", July 30 - August 1, 1997, Gianpaolo Manfrida ed., Firenze, Italy, SGE, Padova, 1997, 15

[12] B.H. Lavenda, Thermodynamics of Irreversible Processes, Mcmillan Press, London, 1978

[13] L.D. Landau and E.M. Lifshitz, Statistical Physics, Pergamon Press, Oxford, Part.1, 1980

[14] I. Gyarmati, Non-Equilibrium Thermodynamics, Springer & Verlag, Berlin, 1970

[15] P. Glansdorff and I. Prigogine, On a general evolution criterion in Macroscopic Physics , Physica, 30 (1964) 351

[16] P. Glansdorff and I. Prigogine, Thermodynamic Theory of Structure, Stability and Fluctuations, John Wiley & Sons, New York,1971

[17] I. Prigogine, La fin des certitudes. Temps, chaos et les lois de la nature, Édition Odile Jacob, Paris, 1996

[18] I. Prigogine, Thermodynamics of Irreversible Processes, John Wiley & Sons, New York, 1961

[19] A. Bejan, Advanced Engineering Thermodynamics, John Wiley & Sons, New York, 1988

[20] A. Bejan, Entropy Generation through Heat and Fluid Flow, John Wiley & Sons, New York, 1982

[21] F. Angulo-Brown, M. Santillán and E. Calleja-Quevedo, Il Nuovo Cimento, D17 (1995) 87
 
 
 

- - - - -
 
 
 

[A presentation of the author can be found in Episteme N. 4]

fismat@libero.it