L
=![]() (1)
(1)
(Umberto Lucia)
Abstract
Starting from the results recently obtained in Rational Thermodynamics, the thermo-physical analysis of the dynamics of cancer interaction with the host immune system is developed using the mathematical model recently obtained in literature. A mathematical model to evaluate the growth of the cancer is proposed.
1. - Introduction
The high degree of order displayed by living systems in space and time makes one often wonder about their compatibility with the laws of Thermodynamics, specifically with the Second Law. The tendency of living systems to increase their internal order in the course of their differentiation, growth, development, may appear to be at odds with the tendency of most condensed matter to proceed towards states in which the entropy of the systems is maximized. A living system is not isolated and is not in equilibrium. It is rather an open system, which can exchange matter and energy with the environment. It is in a stationary state, which is not at equilibrium, but which must display stability for times, which are short respect to a lifetime and long with respect to the characteristic times of the internal processes of the system. It can evolve continuously to other stationary states of slightly different structure and function in times comparable to its lifetime [1].
Recently, in Thermodynamics, the basic role of the entropy has been demonstrated in global analysis [2-5] and in the studies of the stability also for the open systems [2,3]. Moreover mathematical results about the analysis of the Thermodynamic stability of the open systems have been recently obtained [3-5], for any non-linear thermodynamic transformation, also when chemical reactions can occur.
In this paper this thermodynamic results are used in the analysis of the dynamics of cancer interaction with the host immune system, described by the more recent mathematical model proposed [6]. As a consequence a mathematical model for the evaluation of the numerical growth of cancer cells is obtained.
2. - Recently developments in Rational Thermodynamics
To deduce a global principle of analysis for the stability of the open thermodynamic systems the initial and the final states have been assumed uniquely defined and stable, and the system has a response time t after which it goes from the initial to the final state. Thus the state functions satisfy the conditions of the calculus of variations [1].
A continuum general system was examined and its partition in its subsystems
with mass dm and volume dV = dm/r,
with r density, has been made [3-5].
For every sub-system the density of the thermodynamic Lagrangian per unit
of time and temperature L
has been defined as:
L
=![]() (1)
(1)
where T is temperature, t time and LT is the thermodynamic Lagrangian. The analytical expression of L is [3]:
L
= ![]() (2)
(2)
where S is the entropy and [3]:
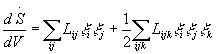 (3)
(3)
with Lij and Lijk symmetric coefficients, and Y, the non-linear dissipative potential density, is expressed by the relation [3]:
![]() (4)
(4)
To obtain the thermodynamic Lagrangian from the relation (2) the integration on total volume V, on temperature T and on time t was done, obtaining, by the analytical expression (3) and the Gouy-Stodola theorem [3], the following expression [3]:
LT =![]() (5)
(5)
where DSirr is the variation of the entropy due to irreversibility.
Thus, as a consequence of the principle of the least action [3], the following result was obtained [3-5]:
d(DSirr) = 0 (6)
and during the thermodynamic path from the initial to the final stationary state [3-5]:
d(DSirr) < 0 (7)
As a consequence the non-linear principle of stability for the open systems' stationary states has been obtained; this states: "the non-linear mathematical condition of stability for the open systems' stationary states consists of the maximum for the variation of the irreversible entropy function, in the response time of the system" [3-5].
3. - The mathematical fundamental for the dynamics of tumor interaction with the host immune system
To describe the dynamics of cancer interaction with the host immune system a kinetic or Boltzmann-like theory is considered. This can describe the non-equilibrium evolution of a population of several interacting populations referred to the physical system. This system is constituted by a cancer which grows in vivo and interacts with the host immune system. The host system has the potential capability of producing some significant anti-cancer reactions, since it can recognize cancer-associated membrane antigens or mutated peptides presented histocompatibility complex [1,6-8]. The cellular interaction can be modelled by the evolution equations for statistical variables related to the distribution over physical states which characterize the various interacting populations [6-8].
The axiom, which are the fundamental of the mathematical theory, are [7]:
Axiom 1. - The physical system consists of cells belonging to n interacting populations, each denoted by the subscript i, with i =1,...,5, where i = 1 corresponds to the cancer cells, i = 2 to the cells of the feeding host and i = 3 to Polymorpho Nuclear Leukocytes, i = 4 to Lymphocytes and i = 5 to Macrophages.
Axiom 2. - The physical state of each cell is described by the variable u, the activation state, whose values span in the interval [0,1]. The statistical of the state of the whole system is defined, for each of the n populations, by the number densities
Ni = Ni(t,u) : [0,T] ´ [0,1] ® R+ (8)
where Ni(t,u) du defines the number of cells of the i-population which, at the time t, are characterized by an activation in the range [u, u + du]. The state of the whole system is defined by the whole set of number densities {N1,...,Nn}Ni³ 0. The number of cells in the same volume at time t is defined by:
n(t) = ![]() (9)
(9)
Axiom 3. - Encounter between pairs can be divided into conservative encounters, which preserve the total number of cells and are characterized by transition of state, and proliferative encounters, which are characterized by increase or decrease of the number of individuals. Conservative encounters occur between cell pairs, from the same or different populations, and have transition rates of the type:
Aij(v,w;u) = hij(v,w) yij(v,w;u) (10)
where Aij(v,w;u), elements of the n ´ n matrix A, denotes the number of encounters per unit volume and unit time between cell pairs of the (i,j)-populations with states v and w, and transition into the state u; hij(v,w), elements of the n ´ n matrix h, is the encounter rate, which denotes the rate of such encounter; yij(v,w;u), elements of the n ´ n matrix y, is the transition probability density, which denotes the density of the probability distribution of such encounters and transition into the state u. Proliferate encounters occur between cell pairs of the same or different populations, and generate a proliferation or destruction rate in the i-population of the type:
![]() (11)
(11)
where sij, elements of the n ´ n matrix s, denotes a term which will be defined proliferation-destruction rate coefficient. The elements sij of the n ´ n matrix s can be written as:
sij(u,v) = bij(u,v) dij (12)
where (see Table I):
 (13)
(13)
and dij must be evaluated experimentally.
Axiom 4. - The number of encounters per unite time in the volume, between cells of the (i,j)-populations with states (u,v), is proportional to the product Ni(t,u) Nj(t,v).
Axiom 5. - An external action ji(t), which may depend on t, can be defined in such a way that it acts directly on the rate growth of u related to Ni
![]() (14)
(14)
Axiom 6. - Generation from the bone marrow will be equivalent to the death of unstimulated cells. The artificial addition of cells from each population is simulated by the source terms gi(t,u).
4. - The thermo-physic and mathematical model
In this Section it will be obtained the result of the application, of the theorem of maximum for the entropy due to irreversibility in the open system [11], to the dynamics of tumor interaction with the host immune system.
The irreversibility consists of the proliferation or destruction rate in the population caused by the encounters between cell pairs of the same or different population. This is expressed by the proliferate encounters (11). As a consequence the variation of the entropy due to irreversibility DSirr is directly proportional to this term:
DSirr = constant Si(t,u) (15)
Now, applying the maximum principle (6), it follows:
dSi(t,u) = 0 (16)
which, considering bij and dij constant, becomes:
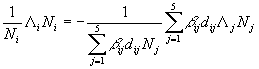 (17)
(17)
where Lk is the following differential operator:
Lk = ![]() (18)
(18)
From the differential equation (17), the following two first order differential equations system can be obtained:
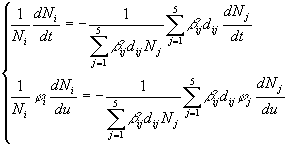 (19)
(19)
To solve this mathematical problem it is necessary to deduce a model for the variable u as a function of time, j and d, starting from the experimental data. Here, to obtain an analytical first order approximated solution, the mathematical problem can be solved assuming that the two differential equations are independent and that j and d are constant. As a consequence it follows that, for the first equation, the solution is:
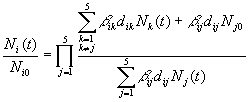 (20)
(20)
and, for the other one, it results:
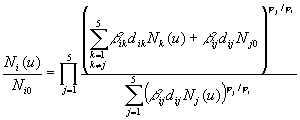 (21)
(21)
where Nk0 are the number of cells at the initial time.
From these relations (20) and (21) it is possible to argue that:
1) cancer growth is a function of the time behaviour of the immune system;
2) cancer growth depends on the statistical distribution of the tumour and the immune cells;
3) cancer cells proliferation or destruction depends on the interaction between tumour and immune cells and between the different immune cells themselves;
4) cancer growth is a function of the u-state behaviour of the immune system;
5) cancer cells proliferation or destruction depends on the u-state change velocity rate (jj/ji) between the u-state changes velocity j of the immune and of cancer cells.
As a consequence of these considerations about the first order solution obtained, it follows that cancer cell is an adaptative system, able to change its u-state and the u-state change velocity as a function of the external conditions and the interactions with the immune system.
5. - Conclusion
The dynamics of cancer interaction with host immune system has been analysed using the more recent mathematical model and applying the principle of maximum entropy variation due to irreversibility. A two first order differential equations system (19) has been obtained to evaluate the numerical density variation of the cancer and immune cells during their interaction. A first order solution of this differential equations system has been obtained. It follows that cancer growth is a function of the time behaviour of the immune system, it depends on the statistical distribution of the cancer and the immune cells, it is a function of the u-state behaviour of the immune system, cancer cells proliferation or destruction depends on the interaction between cancer and immune cells and between the different immune cells themselves, it depends on the u-state change velocity rate between the u-state changes velocity of the immune and cancer cells.
As a consequence it can be argued that cancer cell is an adaptative system, able to change its inner state and its inner state change velocity as a function of the external conditions and the interactions with the immune system.
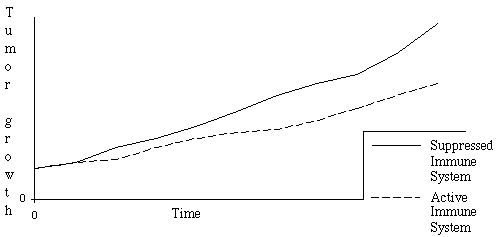
In Figure 1 represents the qualitative shape of the behaviour of two
kind of cancer, whose data can be found on Ref. [7]: a highly aggressive
and poorly immunogenic cell line established from the first in vivo transplant
of the moderately differentiated mammary Aden carcinoma that spontaneously
arose in a 20 month old multiparous BALB/c mouse and a poorly immunogenic
methylcholantherene induced sarcoma of BALB/c mice. The shapes obtained
agree with the experimental shapes reproduced on Ref. [7].
References
[1] M. Cerdonio and R.W. Noble: Introductory Biophysics, World Scientific, London, 1985
[2] U. Lucia: Physical model for the engineering analysis of the thermoelasticity of solid bodies , Chinese Journal of Mechanical Engineering, accepted, in printing
[3] U.Lucia: Mathematical consequences of the Gyarmati's Principle in Rational Thermodynamics, Il Nuovo Cimento B, Vol.110, N.10 (1995) 1227-1235
[4] U. Lucia: Irreversibility and entropy in Rational Thermodynamics, Ricerche di Matematica, in printing
[5] U. Lucia: Maximum principle and open systems including two phase-flows, Rev. Gén. Therm., 37 (1998) 813-817
[6] M. Fabrizio: The concept of dissipation in complex systems , Ricerche Matematiche, XLI, Supplemento (1992) 123-132
[7] N. Bellomo and G. Forni: Dynamic of Tumor Interaction with the Host Immune System, Mathl. Comput. Modelling, 20, 1 (1994) 107-122
[8] P. Van der Bruggen, C. Traversari, P. Chomez, C. Lurquin, E. De
Plaen, B. Van den Eynde, A. Knuth and T. Boon: A gene enconding an antigen
recognized by cytolic T lymphocytes on a human melanoma, Science, 254
(1991) 1643-164
- - - - -
Table I - bij coefficients (see Ref. [7])
| j: i: |
|
|
|
|
|
| 1: Tumor |
|
|
|
|
|
| 2: Envir. |
|
|
|
|
|
| 3: Leuk. |
|
|
|
|
|
| 4: Lymph. |
|
|
|
|
|
| 5: Macroph |
|
|
|
|
|
Figure 1 - Qualitative shape for the cancer growth as a function of the immune system answer (cancer data from Ref. [7])
- - - - -
[A presentation of the author can be found in Episteme N. 4]
fismat@libero.it