A recent history of mathematical applications
(Umberto Lucia)
1. - Introduction
During the last three decades, computer modelling and mathematical simulation have become increasingly important in cybernetic and physics applications to physiology models. In fact mathematical modelling has been shown to be a substantial tool for the investigation of complex systems and their dynamics, and moreover, since the level of complexity it is possible to model parallels existing hardware configurations, primarily tuned to memory, disk capacity, and CPU speed advances in computer technology have made possible their application to the computational models of complex living systems. For these reasons, the computational methodology has taken hold in medicine and has been used successfully to suggest physiologically and clinically important scenarios and results [1]. The goal consists in understanding which of the system's characteristics and interactions are essential in order to quantify and represent its behaviour: such results may help to describe known behaviour as well as predict unknown responses and may suggest new representations.
In this paper, the aim is to show a methodological technique to solve the inverse problem in electrocardiography (ECGraphy); to do so the fundamental of modelling and simulation technique, which can be applied to a class of bioelectric field problems, will be described.
It will be analysed a class of direct and inverse volume conductor problems which arise in electrocardiography [2-5]. The solutions to these problems have applications to defibrillation studies, detection and location of arrhythmia, impedance imaging techniques, and localization and analysis of spontaneous brain activity in epileptic patients; furthermore, they can, in general, be used to estimate the electrical activity inside a volume conductor, either from potential measurements at an outer surface, or directly from the interior bioelectric sources.
It will be described the recent history of the mathematical models used in the cybernetic interpretation of physiological input in the direct problems.
2. - Myocardium electric volume conductors
A general volume conductor can be defined as a region of volume, W, with conductivity, s, and permittivity, e, in which it resides a source current per unit volume, Iv.
Solving a volume conductor problem means to find the expressions for
the electric field, ![]() , and
potential, F, within the volume, W,
or on the boundary surface, G.
, and
potential, F, within the volume, W,
or on the boundary surface, G.
The bioelectric current sources, Iv, arise from excitable cells undergoing an activation process: for cardiac tissue, it can be characterized as the process in which the cells undergo rapid depolarization. The depolarization process causes a propagation of excitation waves to move through the myocardium and, as a consequence, these waves produce an extracellular potential field, F. This potential field can be characterized by [1-6]
i - the geometry of the volume conductor
ii - the conductivity of the volume conducto
iii - the distance from the source current, Iv
iv - the orientation of the source current, Iv
v - the intensity of the source current, Iv.
For the macroscopic volume conductor problem, in which the individual
membrane currents are not considered, it is possible to apply a quasi-static
approximation. Because the displacement current, jweE,
with j =![]() , is much
smaller than the conduction current, sE,
the propagation effects are negligible, and inductive effects are dwarf
[5].
, is much
smaller than the conduction current, sE,
the propagation effects are negligible, and inductive effects are dwarf
[5].
In this case, the more general analytical form consists of a reduction
of the Maxwell's equations to Poisson's one for electrical conduction:
In this form, the source region and an understanding of the primary
bioelectric sources, Iv, are considered in the form of
a simplified mathematical model.
Alternatively, it is possible to define a boundary surface around the
region which includes the sources and recast the formulation in terms of
information on that surface, finding the following Laplace's equation:
Now, these equations must be solved considering appropriate set
of boundary conditions.
The associated boundary conditions depend on the type of problem one wishes to solve.
Here, the direct problem will be solved respect to F,
with a known description of Iv and the Neumann boundary
condition:
This problem can be used to solve the direct ECGraphy volume conductor
problems: it is possible to utilize the descriptions of the current sources
in the heart and calculates the currents and voltages within the volume
conductor of the chest and voltages on the surface of the thorax.
The inverse problems associated with these direct problems involve the estimation of the current sources Iv within the volume conductor from measurements of voltages on the surface of the thorax itself.
So it is possible to solve the equation considering the boundary conditions:
![]() on GT
(5)
on GT
(5)
The first is the Dirichlet condition, which says that it is possible
to use a set of discrete measurements of the voltage of a subset of the
outer surface, while the second is the natural Neumann condition, considered
before. It does not look much different than the formulation of the direct
problem, so the mathematician Hadamard [7] noticed that inverse formulations
of boundary value problems were often ill-behaved and defined the conditions
for well-posed and ill-posed problems. For a problem to be well-posed in
the Hadamard sense, it must meet the following criteria:
1 - for each set of data, there always exists a solution
2 - the solution is unique
3 - the solution depends continuously on the data.
a - there is not a unique solution; in fact there is a multitude of solutions
b - the solution does not depend continuously on the data; in fact small errors in measurements may cause large errors in the solution.
While many strategies tend to be problem-dependent, there are a few
which are generally applicable to bioelectric field problems [7-9]: a general
technique for dealing with the problem of nonuniqueness transfers the problem
to be solved into a model problem. One usually breaks up the solution domain
into a finite number of subdomains, in which a simplified model of the
bioelectric source can be described. Once the problem of nonuniqueness
is addressed, there still exists the problem occurring when the solution
does not depend continuously on the data. In these cases, the linear algebra
counterpart to the elliptic boundary value problem is often useful; in
fact the numerical solution to all elliptic boundary value problems can
be written in the form of a set of linear equations as follows [7-9]:
A characteristic of A for ill-posed problems is that it has a very large condition number, so that the ill-conditioned matrix A is very near to being singular. The inversion of a matrix, which has a very large condition number, is highly susceptible to errors. The condition number is defined as k(A) - ||A|| ||A-1|| or the ratio of maximum to minimum singular values measured in the L2 norm. The ideal problem conditioning occurs for orthogonal matrices which have k(A) » 1 , while an ill-conditioned matrix will have k(A) >> 1. The condition of a matrix is relative because it is related to the precision level of computations and is a function of the size of the problem [7-9].
For the ECGraphy problem, voltages could be measured on the surface of the heart and used to calculate the voltages at the surface of the thorax, as well as within the volume conductor of the thorax. The inverse problems are formulated as using measurements on the surface of the thorax and calculating the voltages on the surface of the heart. Here we are solving Laplace's equation instead of Poisson's equation, because we are solving for distributions of voltages on a surface instead of current sources within a volume [7-9].
If this problem is represented as a linear system, by expressing
for the Cauchy problem:
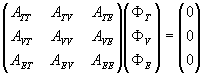 (8)
(8)
where the subscripts, T, V, and E stand for
the nodes in the regions of the thorax, volume, and epicardium.
In general, the ATE sub-matrix is zero, so it is possible
to obtain:
3. - Physiological considerations and cybernetic model
Clinical ECGraphy is concerned with the problem of relating the time-varying potentials measured at the thorax surface to the correlated electrophysiological phenomena in the auricles and ventricles, during the heart cycle.
A detailed knowledge of the intracardiac charge distribution, the electromotive source, and the extracardiac distribution of electric potentials, during the various phases of the heart beat, is essential for a correct understanding of their correlation and the consequently pathologies [10].
The distribution of the potentials in volume conductors was investigated by immersing an isolated turtle heart in a cylindrical Ringer bath [10-12]: electrical recordings allowed the scientists to obtain the instantaneous equipotential maps corresponding to the ventricular activation. The maps showed that [10]:
i - at the beginning of the ventricular excitation, the extracardiac potential distribution is similar to that of produced by a single electric dipole, both near the heart and at the boundary of the medium
ii - the potential maximum is located near the apex of the heart
iii - the potential minimum is located near the base of the heart
iv - during later stages of ventricular activation, the potential distribution at the boundary of the medium is still of the single dipole, while the potential pattern near the heart is much more complicated
v - during the multipolar phases, exploration of the medium near the heart provided information about the probable location of multiple intracardiac excitation waves
vi - the potential distribution and the correlated current distributions
suggested that two groups of active fibres are located in the right and
left parts of the heart, at the end of ventricular activation
As a consequence, it is possible to argue that, during the multipolar
intervals, measurements, taken at increasing distances from the heart,
contain less and less information on the heart activity.
It is of considerable clinical interest to determine whether thorax surface ECGraphy allows to derive local heart information. Maps, representing the instantaneous distribution of the chest potentials, in normal subjects and in cardiac patients, may give significant information about the multiple depolarization waves travelling through the heart walls during the heart cycles, allowing to obtain a method of clinical prevention in cardiac pathologies [10,13,14]. In fact, in heart patient, the number, location and displacement of potential maxima and minima are different respect to those of normal subjects [10,13].
The cybernetic model use to analyse the physiological phenomena is the multipole expansion, which consists of an orthogonal expansion of the thorax potentials in spherical harmonics. To do so, the thorax will be considered as a cylinder with an approximated circular cross section and it will be drawn a sphere defined as follows [6]:
1 - its centre is the symmetry centre of the cylinder
2 - its total area is the same of the cylinder.
Now polar coordinates are introduced defining their origin coincident
with the centre of the sphere, the z axis along the vertical direction
and the origin of the azimuthal angle j
on the middle of anterior chest wall. In this geometry, it is possible
to introduce the spherical harmonics functions Ylm(J,j),
with l = 0, 1, 2, ... and -l £
m
£
l,
defined as [15]:
It has been showed that the electric potential Vt(J,j),
measured at the thorax surface, can be expressed in terms of the spherical
harmonics functions themselves as follows [6]:
The first 64 spherical harmonics provide a very good representation
of the ECGraphy maps, taken with a particular arrangement of the leads
on the thorax, but also the maps taken wearing the lead jacket with any
arbitrary orientation with respect to a prescribed system of body axes.
It can be shown that it is possible to obtain the same representation by using a less number of orthogonal functions introducing the Loéve-Karunen expansion.
A good approximation to decoding the data collected by the leads on
the thorax surface is the one provided by the research of the random variables
which must be not correlated and by which it is possible to write that
the signal f(t) can be represented as follows:
where ck are the uncorrelated random variables,
the
yk the waves forms a priori
unknown and E[f(t)] is the error. At the beginning
everything is unknown, so it is important to introduce a lot of mathematical
conditions. They are [16]:
1 - the set of the waves forms
![]()
must be a set of orthogonal real functions on the definition domain
T
2 - the functions yk are normalized to 1 as follows:
![]() (14)
(14)
3 - the coefficients ck are given by the relation:
![]() (15)
(15)
with fR(t) = f(t) - E[f(t)],
the measured signal
4 - the functions yk are numerated so that the variance of the random variables ck associated to them are in non-increasing order:
![]() (16)
(16)
5 - the yk are such that, if it is considered the truncated series:
the N-th remainder is minimum in quadratic means:
Under these hypotheses the yk
satisfies the homogeneous Fredholm integral equation:
with K(t,t') the correlation function of the
random function, defined as:
The technique of canonical expansion for random fields, the Loève-Karhuen expansion, has been applied to the ECG maps reconstruction as follows [6]:
1 - the measured thorax voltage has been written by the Loève-Karhuen expansion:
![]() (21)
(21)
with
![]() ,
,
average on time and individuals of the measured voltage
2 - Fk(J,j) are normalized orthogonal functions on the domain [0,p]×[0,2p] of definitions of the fields, and are to be determined
3 - gk(t) are random variables evaluated as follows:
![]() (22)
(22)
4 - the Fk are labelled in such a way that the following condition is satisfied:
![]() (23)
(23)
5 - the first N Fk are chosen in such way that:
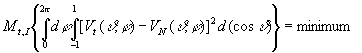 (24)
(24)
It follows that the Fks satisfy homogeneous Fredholm
integral equation:
The results obtained [6] showed that only N = 25 functions are necessary
to describe the ECGraphy signals, so that only 25 leads are necessary to
reconstruct the potential maps with a relative error of 1.5% [6].
References
1 - J.D. Murray. Mathematical Biology. Springer-Verlag, New York, 1989
2 - C.E. Miller and C.S. Henriquez. Finite element analysis of bioelectric phenomena. Crit. Rev. in Biomed. Eng., 18:181-205, 1990
3 - C.R. Johnson, R.S. MacLeod, and P.R. Ershler. A computer model for the study of electrical current flow in the human thorax. Computers in Biology and Medicine, 22(3):305-323, 1992
4 - C.R. Johnson, R.S. MacLeod, and M.A. Matheson. Computer simulations reveal complexity of electrical activity in the human thorax. Comp. in Physics, 6(3):230-237, May/June 1992
5 - R. Plonsey. Bioelectric Phenomena. McGraw-Hill, New York, 196
6 - L.F. Favella: Methodological and mathematical problems in ECG analysis. Cybernetics and Systems, 15: 169-196, 198
7 - A.N. Tikhonov and A.V. Goncharsky. Ill-Posed Problems in the Natural Sciences. MIR Publishers, Moscow, 198
8 - V.B. Glasko. Inverse Problems of Mathematical Physics. American Institute of Physics, New York, 198
9 - Y. Yamashita. Theoretical studies on the inverse problem in electrocardiography and the uniqueness of the solution. IEEE Trans Biomed Eng, 29:719-725, 198
10 - B. Taccardi and G. Marchetti. Distribution of heart potentials on the body surface and in artificial conducting media. Proceedings of the meeting "Electrophysiology of the heart", 11-13 october 1963, Pergamon Press, London:257-280, 196
11 - B. Taccardi. La distribution des courrants d'action du coeur de tortuedans un milieu conducteur à trois dimensions. Arch. Int. Physiologie, 64: 114, 195
12 - B. Taccardi. La distribution spatiale des potentiels cardiaque. Acta Cardiol., 13: 173, 195
13 - B. Taccardi. Analisi qualitativa del campo elettrico cardiaco. Bollettino del "Centro G. Zambon" dell'Università degli Studi di Milano 2: 53-70, 1966
14 - T. Winsor. L'elettrocardiogramma nell'infarto del miocardio. Simposi clinici 9: 3-29, 197
15 - L.I. Schiff. Quantum mechanics. McGraw-Hill, New York, 196
16 - L. Favella and G. Morra. Application of Loève-Karhunen expansion to acoustic diagnostic problems for internal combustion engines. Cybernetics and Systems 14: 55-74, 1983
- - - - -
[A presentation of the author can be found in Episteme N. 4]