Looking for Special Relativity's
Possible Experimental Falsifications
(Umberto Bartocci)
1 - Introduction
We already had the opportunity to describe, in the Letter... which opens this special number of Episteme, the fundamental reasons which should inspire a general criticism of relativity, or, better, of the "philosophy" which was (and is) the ground of Einstein's success. This paper is an attempt to analyse the strictly physical (phenomenological) situation, in order to give a suggestion where to look for possible experimental falsifications of the theory (from now on SR, special relativity1), in the conviction that this is the only possible manner to show that the main assumption of "abstract physics" supporters is wrong: namely, that the renouncing to ordinary space, time, causality, was not a "nihilistic caprice", but a necessity forced by facts2.
This analysis is not so easy as it could appear, since to decide whether a given experiment, or phenomenon (two paradigmatic examples: annual stellar aberration, Sagnac's experiment), could be explained in a relativistic manner or not (or else, from the other side, that it could not be explained in a "classical" way), is an engagement which can be pursued only with a great care, and a good knowledge of the theory one is aiming to prove or to disprove3.
Our main points will be that:
I - There are not so many convincing (direct) experimental arguments in favour or SR, as it is vice versa usually emphasized by "orthodox" physicists - which sometimes add, on these premises, that a pretended phenomenon possibly disproving SR would be like a vox clamantis in deserto, and that this justifies the cautious establishment's response in front of such claims.
II - Moreover, there is not even a crowd of experimental data against Einstein's physics. In simple words, we do not have until now enough evidence in favour of neither a point of view, which shows that it would be rather unwise, at least for the moment, to dismiss all attempts aiming to provide a "rational" description of how Nature works.
1.A Cartesian Physics vs Special Relativity
In order to achieve our goal, let us give a sketch of what relativity essentially is. First of all, it is a theory which, contrarily to the common opinion, should be considered more conservative than revolutionary in its essence. In order to explain this assertion, we must go back to the very beginning of physics as a science, and to the opposition between Cartesian conception of space as a plenum, and Newtonian contrary point of view4, an empty space not endowed of any physical objective, measurable, property. Of course, from this quite simple starting point5, divergences grow up in an increasing complexity, but the substance of all conflict is there. After the success of Newton on Descartes, the image of the empty space - in which a mysterious action at a distance ruled the trajectories of all celestial bodies, and in which movement could only be relative, according to Galileo's famous ship's argument6 - dominated the scene of science for more than one Century. The conception of a space acting as an indispensable medium for all physical interactions, came back during electromagnetic studies in XIX Century: Ampère, Oersted, Faraday, Neumann, the great Maxwell's Treatise, etc.. At the end of that Century the situation in theoretical physics was indeed an uncomfortable one. There was the image of the world given by Newtonian mechanics, which marked, even in a symbolical way, the "victory" of science over the supporters of darkness and superstition. But there was an aether too, which was clearly "seen" for instance in the lines of force surrounding a magnet. When Einstein appears on the stage7, a solution was really needed, and there were only two possible way out. Either to accept the evidence for an electromagnetic aether, to refuse the principle of relativity (from now on PR), and to frankly acknowledge that Newton's party was wrong; or, at the contrary, to maintain the foundation of Newton's physics8, even in a quite different space-time set up, really undreamed of until Einstein's age (and this would be the "revolution").
It is obvious that, from our point of view, the really true courage would have been to choose the first option, while Enstein did exactly the opposite. He maintained Newton's empty space, proposing PR as one of the essential Nature's laws, and at the same time "borrowed" from aether's physics concepts like the independence of light's speed from the speed of the source, the finiteness of the speed of propagation of all aether's "disturbances" (fields), etc.. He showed in such a way that it was possible to assemble a general theory, but he was forced, however, to give up ordinary space and time conceptions. Thus, it is not a "paradox" to assert that Einstein followed rather closely Newton's tracks9, and that its only true opponent is Cartesian fluid-dynamical physics10. One could as well assert that SR is similar to a proof ab absurdo: the only way to keep together the abstract RP, and the experimental electromagnetism, is to abandon ordinary space-time, and since this is absurd, we must choose between the principle and the facts. Needless to say which should have been, in our opinion, the right choice.
1.B Special Relativity's True "Heart"
As we have mentioned, SR is made up of two postulates (Voraussetzungen), RP plus LSP (Light's Speed Principle)11. In an empty space RP is "acceptable", because of a kind of insufficient reason principle: there is no reason why an inertial observer12 should experience a physics different from another one, seeing that there exists nothing which could decide which one is really moving, or still. In an aether theory, and in a wave theoretical approach to the nature of light (perhaps not the only possible one), LSP is acceptable (even in a stronger form, see the next section 4). So, from the point of view of a critic of SR, this is 50% correct, and it is not LSP the assertion which should require a careful scrutiny, but SR's true foundation, that is to say PR13. Indeed, it is PR which, added to LSP, makes LSP quite counter-intuitive, and such that all the attention of people goes to the very qell known strange features of relativistic speeds, but, we repeat it, LSP has nothing wrong in itself, and it becomes "bad" when one changes the independence from the speed of the source with the independence from the speed of the observer!
At this point, the fundamental question is: which are the direct experimental arguments in favour of PR?
We believe that an "honest" answer should be, at least for the moment being, that there are not. The greatest part of the pretended experiments in favour of SR - whose correctness one could even accept, mostly if he is not a professional physicist, like the present writer - could be, first of all, easily re-interpreted in an aether theory, finding in fact in such a context their better (proper) "explanation" (the "increasing" of the inertial mass as a phenomenon of "resistance"; the finiteness of the speed of propagation of interactions, perhaps equal for many different phenomena, the consequent "retardation", etc., obvious; for the so-called "time dilation", see the next section 3; and so on, we must confess that we find most of all worth of some attention the claims about the experimental validity od the so-called transverse Doppler effect). Second, that part of experiments which seem to validate PR, have only used the hypothetical motion of the Earth through the aether14, thus showing that theoretical physics has not made, in this field, a great progress since XVII Century! The possibility that this motion does not exist at all - or that it is too small to be detected15 - is seldom taken into consideration in popular divulgations of Einstein's theory, while Descartes-Leibniz's vortex theory16 implies exactly this inexistence. Only experiments performed in reciprocally moving laboratories would give some evidence in favour of the one or of the other conflicting points of view, and these experiments have been almost never done17! In 20 years study of this problem, and innumerable discussions with colleagues (usually worried to avert a friend from bad companies), the author has never heard of such experiments, while at the contrary everybody claimed that it was practically impossible to reach those speeds which could have been significant in order to test RP. Moreover, they added that the required accuracy of measures would have been irreparably disturbed by the forced movement (see even Marinov's remarks, in the next section 2.A).
And so then? Why one should believe in something which has not yet been proved beyond a shadow of a doubt18??
It is at this point unavoidable the doubt that the motivations of Einstein's followers are not of a strictly scientific nature (mathematicians for instance greeted with enthusiasm the "birth" of SR, since it showed that their sophisticated tools would have shown their practical utility too19), and we feel obliged to carry on a long research work like the present one.
1.C The Theory of the "Dragging Aether"
It is clear from the above that the general theory which we feel the most trustworthy opponent of SR is the so-called theory of the dragged aether20, a denomination which shows nevertheless an implicit relativistic conditioning. If we consider a physically active aether, why should we accept - in obedience to the opinion that any motion could not be but relative - that it would be the same thing to say either that the aether is dragged, or that the aether is dragging, as it is quite more likely? This misunderstanding is not only of a linguistic nature, since it is at the origin of a pretended "proof" against the theory we are aiming to propose as the possibly "true" one. As a matter of fact, most text-books recall the famous Fizeau's experiment as a "crucial" one proving that the aether is not (at least completely) dragged by moving bodies (in this case water, forced to move in a pipe), but this has really nothing to do with Descartes-Leibniz's theory21!
At this point one could ask whether there are other arguments against the dragging aether (the usual name for an hypothesis of this kind is Stokes theory, but we believe, as we have said, that we are in front of similar but different theories), and one would be perhaps surprised acknowledging that, according to the well known Resnick's book22, only Fizeau's experiment and annual stellar aberration are quoted as such "proofs". Of the first one we have just said, the other one appears as a possible new great misunderstanding, one of the many which affect theoretical physics, which the author, not accustomed to this kind of situation in mathematics, discovered with great amazement23. As a matter of fact, it has been shown very clearly by Giancarlo Cavalleri et al.24: "Some special relativity textbooks assert, without giving a detailed history of the question of aberration, that Stokes theory is wrong [...] their argument is grounded on a misunderstanding: precisely, the aether which they consider is not irrotational". Moreover, we feel that is not even impossible to explain Bradley's aberration introducing a "model" similar to the local magnetosphere (quite compatible with the general theory of the dragging aether) discussed in the reprint of Zapffe's paper in this same volume, namely, that this question is still well open.
This is the general conceptual frame25 in which one should fit the observations and proposals below, which represent a kind of Summa, trying to collect the "best" acquired in many years research and frequentation of "alternative physicists", to whom all (dead or alive) go the author's warmest thanks.
2 - Does RP Hold in Electromagnetism?
We begin our analysis restating the fundamental question in more specific words: does electromagnetic phenomenology really allows physicists to propose RP as one of the most fundamental Nature's "laws"?
It is obvious that, from the point of view of the "Cartesian physics" sketched in the previous section, the expected answer of Nature should be a clear and strong not, and not only in electromagnetism, but in principle even in mechanics, with the only difference that it is very likely that mankind has not been able to observe until now significant mechanical violations of RP, as men have been confined in their small planet, and in the realm of "low velocities".
It is rather instructive to quote at the opposite the words of a physicist (taken from an Internet group discussion), who claims that:
The experimental evidence confirming the principle of relativity is actually overwhelming, in the sense that in no field has one ever discovered any dependence of the forms of the laws of physics on the velocity of the reference frame.
Is this an opinion, or objective science (as far as science can be objective in the limits of our present knowledge)? The fact is that exactly Maxwell's Electrodynamics (from now on ME), the supposed pillar of Einstein's SR26, provides a mathematical set-up which can have different interpretations as a physical theory (which is a mathematical theory, plus a set of more or less explicit, and formalized, assumptions, rules of codification and decodification, from the reality to the abstract intellectual "model", and conversely, which are not so rigid), some of which interpretations do not satisfy RP.
To this question the author has dedicated a paper27, in which it is shown that the phenomenon of the electromagnetic induction, the only one which Einstein choosed as a motivation for his proposal of a complete symmetry between "inertial frames", is indeed a good example (internal to ME) of a symmetrical interaction28, but it should have been regarded as an exception (which has to do with the circumstance that we are in this case in front of closed circuits) in classically interpreted ME, and not as a rule. As a matter of fact, general Maxwell's treatment (which is "aether-based") suggests instead that we are possibly in front of an asymmetrical phenomenology, in which velocities with respect to a priviliged frame make a great difference. One must admit, of course, that SR show how it is possible to interpret ME even in a conceptually symmetrical framework, but one should admit too that we are indeed in front of two different physical theories, even if they are "sharing" the same equations. Which one is "true", we actually do not really know. Physics is believed to be above all an experimental science, but the most meaningful and widespread convictions appear to be more theoretical in essence (we do not want to say: ideological) than experimental, and it was really a surprise to realize that some endless discussions could have been put to an end with experiments that nobody has ever properly done (but almost every physicist thinks, and acts, as if they had been done!).
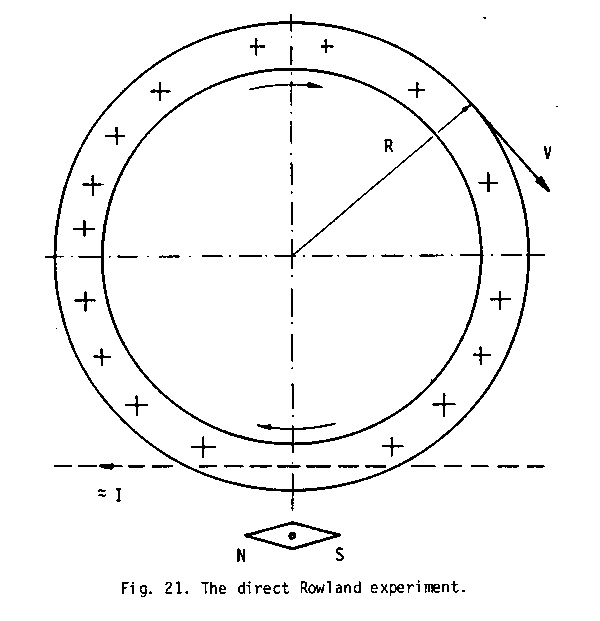
2.A The Direct and the Inverse Rowland Experiments
It seems convenient, for many reasons, to start with an "experiment" which could be thought of as the possible key for understanding the nature of the eventual electromagnetic asymmetries we are talking about. The dear unforgotten friend Stefan Marinov explains the situation is his Divine Electromagnetism (1993), pp. 169-173, and we quote below some of his very clear words.
Rowland [Rowland H.A., Sitzungsberichte der K. Akademie
der Wiss. zu Berlin, p. 211 (1876)] carried out in 1876 the following
experiment: A disk was charged with positive (or negative) electricity.
There was a magnetic needle in the neighbourhood of the disk. When the
disk was set in rotation, the needle experienced a torque due to the magnetic
action produced by the convection current of the charges rotating with
the disk. I call this the DIRECT ROWLAND EXPERIMENT.

According to the principle of relativity, if the disk
will be kept at rest and the needle will be set in rotation, the same torque
has to act on it. Such an experiment is called by me the INVERSE ROWLAND
EXPERIMENT.
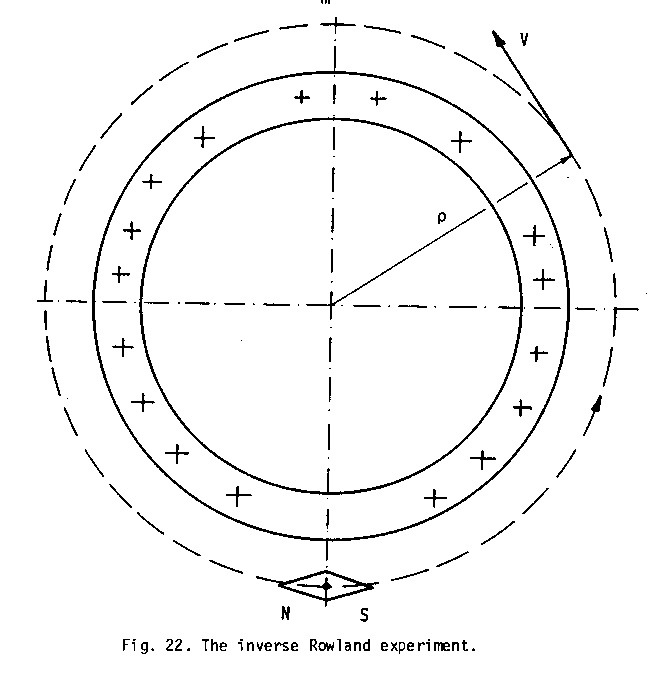
[...] The above two experiments can be called ROTATIONAL Rowland experiments. It is easy to transform them into INERTIAL experiments. So if we charge a conveyer belt and set it in action, the motion of the charges can be considered as inertial (i.e., with a velocity constant in value and in direction) over a considerable length of the belt and we shall realize thus the inertial direct Rowland experiment.
[...] As far as I know nobody has carried out either the rotational nor the inertial inverse Rowland experiments.
Now I shall show that, contrary to the prediction of the princople of relativity, the inverse Rowland experiment must be null, i.e., a magnet moving with respect to charges at rest does not experience torque.
[...] I carried out the rotational direct and inverse Rowland experiments. [...] Of course, because of the mechanical vibrations and the Earth's magnetism, it was pretty difficult to establish such a null effect and my experiment, naturally, needs confirmation carried out in a first class laboratory. According to me, the inverse Rowland experiment has been not carried until now not because of technical difficulties but because of a fear that the result will be null [...]
Marinov's words describe a situation which we will face later on in other conceptually similar contexts, but we wish to remark since now that, apart from possible theoretical and experimental questions arised by the "Rowland case"29, they testify our same experience: direct fundamental experiments, the only ones which should allow Einstein's enthusiasts to assert that SR is really beyond a shadow of a doubt, have never been performed30!
2.B Some Theoretical Remarks About ME
Before going on, it is convenient to be more precise about ME as a mathematical theory. By this we mean the system of the four Maxwell's equations (expressed in standard differential notation, in the MKSQ unit system):
(1) curl(E) = -![]()
(2) curl(B) = m
0 (e
0![]() + j)
+ j)
(3) div(E) = ![]()
(4) div(B) = 0 ,
which can be reduced to the two D'Alembert wave equations for the electric and magnetic potentials F , A :
(5) F = -![]() ,
,
(6) A = -m 0 j ,
where appear the charge density r (x,y,z,t)
and the density current j(x,y,z,t) (which satisfy the charge
continuity equation div(j) = -![]() ).
).
The potentials F , A are connected by the Lorentz gauge condition:
(7) div(A) = -c-2![]() (where: c-2 = e
0m
0 ) .
(where: c-2 = e
0m
0 ) .
The electric and magnetic fields E, B are expressed in terms of the potentials by the equations:
(8) E = -Ñ
F
- ![]()
(9) B = curl(A) ,
and the force acting on a charge q , movin with velocity v , is the Lorentz force:
(10) F = q (-Ñ
F
- ![]() + v´
curl(A))
= q E + q v ´ B .
+ v´
curl(A))
= q E + q v ´ B .
There is indeed in the theory a further assumption, which can be viewed as a restriction on the way fields originate from sources31: we assume that for a given r and j, (5) and (6) have a unique solution which is physically relevant, namely the one given by the so called Liénard-Wiechert retarded potentials:
(11) F (x,y,z,t) = ![]()
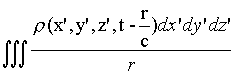 ,
,
(12) A(x,y,z,t) = ![]()
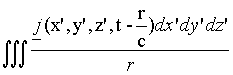 ,
,
where r'(x,y,z;x',y',z') is the ordinary distance ![]() , and the integration is made on the whole space (one gets smooth
solutions if one starts from smooth data for r
and j ).
, and the integration is made on the whole space (one gets smooth
solutions if one starts from smooth data for r
and j ).
The previous formulae (11) and (12) are in truth not so simple to understand.
Their "physical" meaning is that the contribution of a point (x',y',z')
to the integrals is not given for instance by the charge which is
in this point at the time t , but only by the charge which was in
(x',y',z') at the retarded time t - ![]() , that is to say by the charge which is seen from (x,y,z) in the
point (x',y',z') at the time t .
, that is to say by the charge which is seen from (x,y,z) in the
point (x',y',z') at the time t .
The equations introduced above must be thought of - in ME's classical interpretation - as valid only in a set of privileged reference frames K , the so-called aether frames (in principle they are unique up to spatial rotations and translations, and up to a time homothety, but do not forget what has been said in footnote 25), where the ordinary concepts of classical mechanics can be used. In their relativistic interpretation, one must add an additional hypothesis, which ensures the validity of the theory in all inertial reference frames K' , namely the ones moving with a uniform velocity with respect to K (connected to K by means of a Lorentz-Poincaré transformation):
(13) (j,r c) and (cA,F ) are 4-vectors of the Minkowski space-time.
Only this assumption enables to write the Maxwell's equations in a covariant form, but one must remark that (13) is a genuine new physical assumption, which is logically independent of the previous ones, and that it is perfectly legitimate to use ME in a "classical" space-time theory without any connection at all with relativity. We shall show now some of the differences which can arise between different physical interpretations of the same mathematical theory.
2.C Trouton-Noble Type Experiments
Let us study more carefully the different previsions which a Cartesian and an Einsteinian physicists (from now on: C and E ), can do with the same mathematical theory.
Let K(x,y,z,t) be an inertial coordinate system of the space-time. K will mean for C a (possibly local) rest-frame in the aether (or even an aether-frame). Measures of space and time (for instance, synchronizations of remote clocks) can be made exactly as Einstein requires, so that even E can accept K as one of his inertial coordinate system. Until this moment, the only difference is that C would not accept as a "good" coordinate system any other similar system K' which would "move" with respect to K with a uniform velocity, and most of all that C would not accept the method that E could indeed use (rightly, from his point of view) in order to simplify the effort to give an answer to some theoretical questions. Namely, to change the coordinate system, choosing another one K' more "suitable" with respect to the physical situation under discussion; make computations in K' ; then go back to K using some coordinate transformation (in the present case, Lorentz-Poincaré transformations). In other words, C cannot use sometimes of the facilities of E , but it does not really matter, since they agree at least in the choice of K , and most of all in the system of equations that they have in order to describe electromagnetic phenomenology.
Let us think of an electric charge Q moving in K with some uniform velocity
v = (v,0,0) along the x-axis (let us even suppose that x = vt , y = z = 0 , are the equations of the motion of Q ), and let us ask, to both C and E : which are the electric and magnetic potentials associated with Q ?
The question is such that both C and E will give the same answer32:
(14) F
Q = 
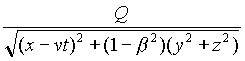 ,
,
(15) AQ = ![]()
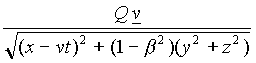
(where, as usual, b = ![]() ).
).
The coincidence of these potentials both for C and E , which could be extended to any system of a finite number of charges (since we are in front of a linear theory), could make believe that C and E would share even the same "physics", at least in the electromagnetic field, but this is not true, as we should immediately understand, now and later in the next section.
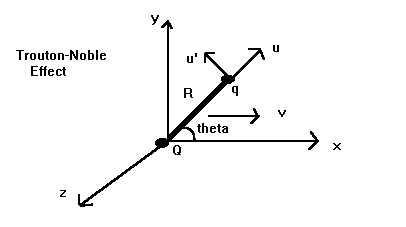
Let us in fact introduce another charge q , in the (xy)-plane, which
in the instant t = 0 has coordinates (Rcos(q
),Rsin(q ),0) , as in the following picture,
and let us ask which is the total electromagnetic force acting on q in
virtue of Q in the case q is supposed to move with velocity w =
(w,0,0) parallel to v (in particular, comoving with Q with
the same velocity v , or standing still in K , case w = 0
) :
Starting from (10), namely, in our case, Fq = q (-Ñ
F
Q
- ![]() + w´
curl(AQ))
, straightforward computations give the following values for the three
terms in the right hand side of the previous expression of the required
force:
+ w´
curl(AQ))
, straightforward computations give the following values for the three
terms in the right hand side of the previous expression of the required
force:
-Ñ
F
Q
= 
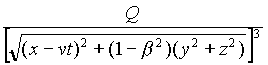 (x-vt,(1-b
2)y, (1-b
2)z)
(x-vt,(1-b
2)y, (1-b
2)z)
-![]() = -
= -![]()
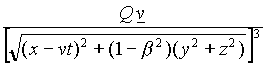 v(x-vt)
v(x-vt)
curl(AQ) = ![]()
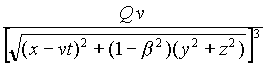 (1-b
2) (0,-z,y)
(1-b
2) (0,-z,y)
w´
curl(AQ))
= ![]()
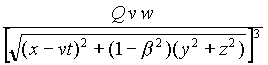 (1-b
2) (0,-y,-z)
(1-b
2) (0,-y,-z)
and so, remembering that ![]() =
=  :
:
(16) Fq = 
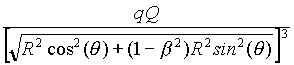 (Rcos(q ),(1-b
2)Rsin(q
),0) +
(Rcos(q ),(1-b
2)Rsin(q
),0) +
- 
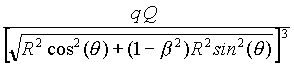 b
2
Rcos(q ) ix +
b
2
Rcos(q ) ix +
+ 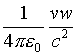
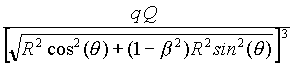 (1-b
2) (0,-Rsin(q
),0) =
(1-b
2) (0,-Rsin(q
),0) =
= 
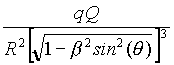 (1-b
2) [ (cos(q
),sin(q ),0) -
(1-b
2) [ (cos(q
),sin(q ),0) - ![]() sin(q ) iy ] =
sin(q ) iy ] =
= 
![]()
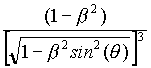 [ u -
[ u - ![]() sin(q
) iy ] ,
sin(q
) iy ] ,
where ix , iy are the unit vectors of x and y , and u is the unit vector of the vector Qq in the instant t = 0 .
This formula gives the exact expression of the required interaction
in ME , with no difference whatsoever whether we are following a classical
point of view or a relativistic one. It is in fact rather instructive,
since it is made up of two terms. The first one, namely 
![]()
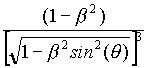 u
, does represent the complete force acting on q when the velocity of q
is equal to 0 , or even when the velocity of Q is equal to 0 , no matter
which is w . When both v = w = 0 , this term is equal precisely to the
well known Coulomb's law for the interaction of static electric
charges.
u
, does represent the complete force acting on q when the velocity of q
is equal to 0 , or even when the velocity of Q is equal to 0 , no matter
which is w . When both v = w = 0 , this term is equal precisely to the
well known Coulomb's law for the interaction of static electric
charges.
For any v , different from 0 or not, this "partial" (if w is not zero) force is "almost" equal - that is to say, up to second order in b - to Coulomb's force, and if we think of a "rigid rod" which connects the two charges Q and q , this term is annihilated by the reaction of the rod.
For our purposes, the interesting term is the other one, which in the comoving case
( w = v and not zero) becomes: -
![]()
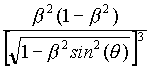 sin(q
) iy .
sin(q
) iy .
This force is not directed along u , so it is not annihilated by the reaction of the rod. Up to second order in b , the projection of this force along the vector
u' = (-sin(q ),cos(q ),0) , namely the unit vector orthogonal to u such that the pair (u,u') has the same orientation as (ix,iy) , is equal to:
(17) -
![]() b
2
sin(q ) cos(q ) u'
.
b
2
sin(q ) cos(q ) u'
.
The "symmetric" computation of the force acting on Q by means of q , always in the comoving case, gives a similar force, but with opposite sign, which implies that we are in the presence of a couple of forces, having linear momentum equal to:
(18) M = -
![]() b
2
sin(q ) cos(q ) iz
= -
b
2
sin(q ) cos(q ) iz
= -
![]() b
2
sin(2q ) iz .
b
2
sin(2q ) iz .
A very "small" momentum indeed, but enough, from the point of view
of C , to let him predict that the rod would turn clockwise (if we
suppose the two charges of the same sign) with respect to z , in order
to reach the equilibrium position parallel to v (for q
= 0 the momentum vanishes, but it vanishes even if q
= ![]() ).
).
This is indeed a violation of the Newton's action-reaction principle, a violation which appears not only in classical electromagnetism, but even in SR (see footnote 29). It appears indeed quite "understandable" in an aether theory, since it would be due to the retardation due to the finite speed of propagation of the electromagnetic interaction. But why have we said: "from the point of view of C ", if we have even asserted that C and E agree with their computation? Because E , the previous formula notwithstanding, is forced to predict that the rod would not rotate! As a matter of fact, C has no other means to ground his prevision of a rotation, while E could argue in the following way too. If I think of an observer X on the rigid rod, then from the point of view of X the rod is standing still, and since X is a "good" observer as I am, then the forces acting on the two charges at the extremities of the rod would be for X exactly equal and opposite, directed along the direction of the rod, as they are for me when v = w = 0 . Since this reference frame K' which I could think of, comoving with the rod, is physically quite equivalent to the one, K , in which I am standing still, and since in K' there should be no rotation (in SR, the action-reaction principle holds in the "proper frame" of the given physical situation), then a rotation should there be not even in K !
This analysis of E is in fact rather easy, but it is not so trivial to understand why E would conclude that, even if the previous momentum in K is indeed different from zero for him too, then the rod would remain nevertheless still. This is why the two forces acting on q and Q at the same instant t in K (we have supposed t = 0 , but it could be any other instant) are not acting in the same instant in K' . That is to say, E thinks that from K we see only an "apparent" momentum, due to the fact that the two forces "appear" to act simultaneously in K , while in the proper system K' , comoving with the rod , the two forces which are "really" simultaneous do not produce a momentum. In conclusion, E would claim that C's prediction is wrong, since he is trying to estimate physical quantities standing far away from the moving object. C could easily object that it is E which is wrong, because when he is thinking of an "observer" E' comoving with the rod, E' would be in motion with respect to the aether ("absolute" motion), and so the Einstein's synchronization of clocks performed by E' is uncorrect. This is the reason why E' believes that the two forces acting simultaneously with respect to him on q and Q do not produce momentum, while they do33.
We have proved that, even starting from the same equations, and making the same computations, there is not a physical agreement between C and E . But who is really right (perhaps no one of the two!)? Thought of a true rod like the previous one, uniformly moving with respect to a frame which one has some right to consider "inertial" (with a "good approximation"), does this rod rotate or not?? An experiment inspired to the situation above was indeed attempted by Trouton and Noble in 1903, and it is one of the few truly electromagnetic experiments aimed to prove the consistence of SR. Unfortunately, Trouton and Noble tried, as usual, to make in evidence a pretended motion of the Earth through the aether, which as we have said very likely does not exist34. To people who are influenced by the rôle of the famous Michelson-Morley optical experiment as one of the principal motivation for the birth of SR, we say that experiments of the previous kind, at the same manner that the one proposed in the next section, aimed to put in evidence the possible electromagnetic effects of the "aether wind" due to an absolute motion, should be regarded as electromagnetic "Michelson-Morley experiments", and that they should be performed for instance in a "train" like the one of the Buys-Ballot's test (see footnote 17).
2.D The Cardone-Mignani Experiment
We have seen in section 2.C that it is not enough to share the same mathematical equations in order to have the same physics. Moreover, even if C and E have a common starting point in Maxwell's equations, to compute the same expressions for the potentials (and for the fields), is not the general rule. We have analysed before a very simple case, in which potentials are indeed equal for C and E , but this agreement does not exist anymore when they are in front of non-uniform motions, like the ones which appear for instance in the case of a circular current.
As an example of this, we suggest to compute (in a given aether-frame K as before; remember what has been said on the "agreement" of C and K about this frame) the force which does act at the instant t = 0 on a test-charge q placed in the center of a circular circuit S , as the effect of a stationary current I flowing in S , when the circuit and the charge are comoving with a uniform speed v = (v,0,0) as in the previous section.
The situation is described in the following picture (the current is supposed to flow in the anticlockwise direction from x to y with respect to z), and so by the parametric motion's equations (both for C and E ):
x = Rcos(q ) + vt , y = Rsin(q ) , z = 0 , 0 £ q £ 2p ,
while the motion's equations of q are obviously:
x = vt , y= 0 , z = 0 :
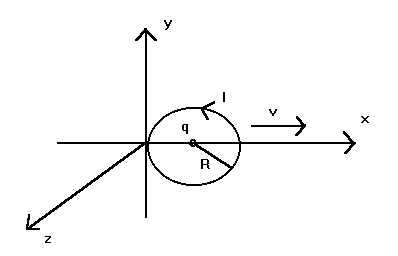
The author did extensively deal with this not simple computation (which requires a direct integration of Maxwell's equations) in the paper quoted in footnote 27, and the result is that the force acting on q , from the point of view of C , is equal to (up to second order effects in b ):
(19) F = -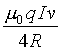 iy
.
iy
.
Thus, C would expect a force which is not equal to zero, and which does depend both on the intensity and on the direction of the current.
From the point of view of E , at the contrary, the prediction is quite different, and he will not agree at all with (19). As a matter of fact, in the proper reference frame K' , comoving with the circuit ( S will be no more circular in K' , but this does not really matter), the 3-force acting on q must obviously be equal to zero ( E maintains the validity of Clausius' postulate in K' ), and this implies that it must be zero even in K .
So the important question is: in which point E , which is using the same Maxwell's equations as C , do not forget it, will differ by the formula (19) when doing his computations in K ?
Here they are, in order to answer precisely to this question, the exact expressions of the potentials of the circuit S computed by C 35 :
(20) F S = 0
(21) AS = ![]() IR
IR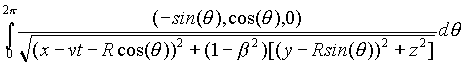 ,
,
and now the expressions of the same quantities as computed by E :
(20') F *S = 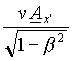
(where Ax' is the first component of the magnetic vector potential in the proper frame K' of S ; we are using the simplest possible case of a Lorentz transformation)
(21') A*S = ![]() IR
IR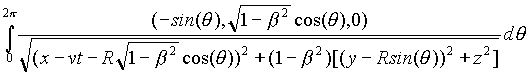 .
.
The great difference between (20), (21) and the corresponding (20'), (21'), is that Clausius' postulate (see footnote 35) does hold in SR only in the proper frame of S , while it is no more valid in K , according to the transformation rules (which are consequences of (13)):
F *S = 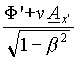 =
= 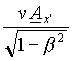
r *S = 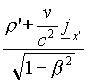 =
= ![]()
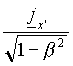
(where the apices designate quantities computed in K' ).
These equations imply that the moving circuit "appears" to have a non-zero density charge in K , and so a non-vanishing electric potential. In classically interpreted ME, at the contrary, the expression for r S is simply given by the general formula:
r (x,y,z,t) = r 0(x-vt,y,z,t) = 0 ,
where r 0 represents the density charge in the case v = 0 .
An analogous "classical" formula describes the relation between the density current terms36:
j(x,y,z,t) = j0(x-vt,y,z,t) + r 0(x,y,z,t) ,
while the same equation, from the point of view of SR, is given instead by:
jx(x,y,z,t) = 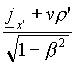 =
= 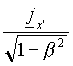
(the other two components of j remains unchanged in the passage from K' to K ).
This shows37 that Maxwell's equations have relativistic solutions only when relativistic treatment of charges and currents is introduced, while they can have equally good "classical" solutions when these terms are defined in a classical way.
Let us remark too that the difference between AS and A*S is "very small", since the two potentials are indeed equal up to second order in b , but that it is not so small to be neglected (see footnote 32), since, in force of (7), one must have (and one has):
div(AS) = - c-2![]() ,
,
div(A*S) = - c-2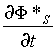 ,
,
and these formulae show that the small difference becomes essential in the second case, when a small term (the divergence of the magnetic potential) is multiplied by c2 , and thus it gives a meaningful non-zero time-variation of the electric potential, a potential which cannot vanish (in the first case, instead, the divergence of the magnetic potential is exactly equal to zero).
In conclusion, we should ask once again: who is really (that
is to say: experimentally) right, C or E ? The aforesaid divergence
can be elaborated in view of the proposal of a new gedankenexperiment
aimed to discriminate between classical and relativistic interpretations
of ME . One could either try to perform direct measures of the force acting
on the charge q , or better of the electric potential difference across
a thin linear conductor T placed along a radius with an extremity in the
centre of C and the other one close to the current wire, as in the following
picture:
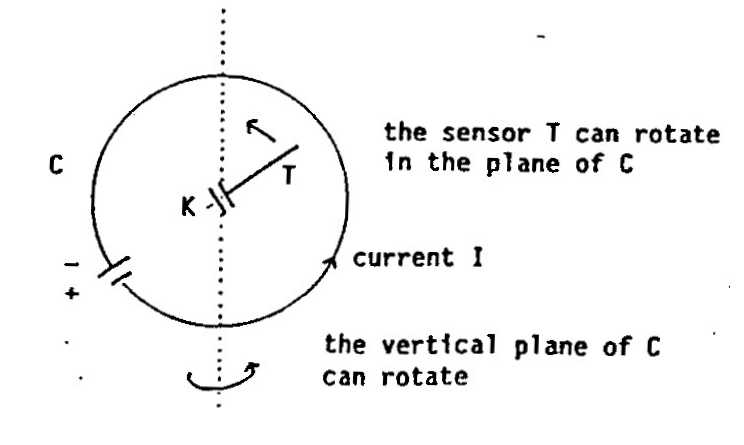
We could attempt to make in evidence a possible Earth's absolute velocity (and this is why the sensor and the circuit's plane have been projected to be able to rotate, since this velocity is unknown), but, as we already said many times, the apparatus should be put in a real motion with respect to an ordinary Earth's laboratory, before saying that this test has given all possible information.
The fact that the force predicted by C does depend both on the intensity and on the direction of the current, should make it possible to separate a non-zero effect from other possible "disturbances" (due for instance to the electromagnetic fields existing in the terrestrial reference frame, and to other sources of systematic errors, or even to the possible non-validity of Clausius' postulate - see footnote 35). Moreover, by increasing I and/or q , one might be able to observe an effect even if the velocity of the moving laboratory is very small, as presumably it has to be, compared with c .
We show below another picture, showing the experimental apparatus which
we38 have tried to use in an amateurish way (in Foligno, near
Perugia, in 1990):
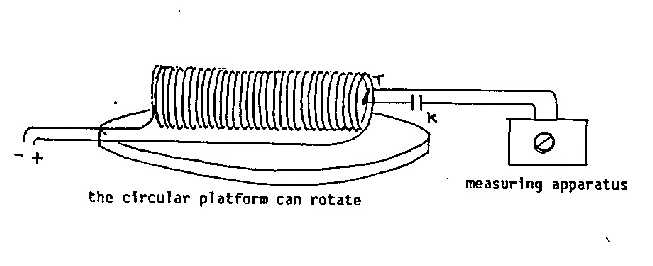
An experiment of this kind has been in fact performed in a professional way by Cardone-Mignani39, with results which are difficult to interpret. Anyway, their apparatus was still in an Earth's laboratory, and so it could have possibly put in evidence only an unlikely "absolute" Earth's velocity.
In conclusion, we want to repeat it once again that:
* - Apart the fact that the most conspicuous phenomena alleged in favour of SR (namely the increasing of the inertial mass and the mean-life of speedy particles) appear rather more compatible with an "absolute theory", than conversely (in absence of any evidence about a symmetry of these phenomena), it is possible to predict from ME physical effects which would depend from an absolute velocity, and this shows that the observation at the beginninf of section 2 - in no field has one ever discovered any dependence of the forms of the laws of physics on the velocity of the reference frame - is wrong (at least from a theoretical point of view, but the assertion appears to be theoretical, and not experimental).
** - Electrodynamical experiments (charges-and-currents) to test SR have been undeservedly neglected, to our actual knowledge, in favour of optical ones, and they moreover (of both kinds) have never (or seldom) been performed in moving laboratories with respect to the Earth.
These statements should "prove" our assertion that SR has not been tested so much as it is usual to claim, by those physicists who appear anxious to persuade their audience that Einstein was the greatest scientist of all times, and that a doubt about SR would be the same as a doubt about the Copernican system40.
3 - An (Impossible?!) Gedankenexperiment with Moving Clocks
There is little doubt that one of the most impressive, and counter-intuitive, consequences of SR, is the so called time dilation, which could be roughly41 expressed as (from the same Internet group discussion quoted before, in section 2):
The lengthening of the period of a moving clock in the ratio g
= 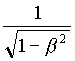 .
.
It would be quite better to say that, for any observer W , the time interval D t which has elapsed for W between two events E , F in its life is equal to:
(22) D
t = 
(where ds2 is the pseudo-metrics of Minkowski space-time),
and that, when expressed in any Lorentz coordinate system K(x,y,z,t) , then (22) becomes:
(23) D
t = 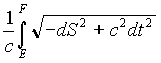 =
= 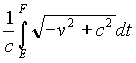 =
= 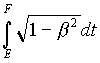 ,
,
since now ds2 = dx2 + dy2 + dz2
- c2dt2 = dS2 - c2dt2
, and where v = ![]() is the
speed
of the observer W with respect to K , and as
usual b =
is the
speed
of the observer W with respect to K , and as
usual b = ![]() .
.
Of course, if this speed is a constant, for instance when W is an inertial observer, then we can write:
(24) D
t = 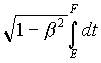 =
= ![]() [t(F) - t(E)] =
[t(F) - t(E)] = ![]() D
t ,
D
t ,
or even:
(25) D t = g D t ,
which means that the coordinate time which has elapsed between the two events E , F is g times the so-called proper time which has elapsed between the same two events with respect to W .
This is all, as far as the mathematical theory of "relativistic time" is concerned. Thereafter it is the moment of phenomena, which go from the observed increasing of the mean-life of speedy particles (with respect to an Earth's laboratory), to the so called twin-paradox, which seems to have been experimentally confirmed by the famous Hafele-Keating clocks' travel around the world (an effect which is more complicated by the presence of a theoretical time dilation due to the gravitational potential, which must be taken into account by people which are confident in relativity, either special or general).
Well, as far as this last experiment is concerned, we share the strong
doubts which are illustrated in the very important paper by A.G. Kelly
listed at the point N. 17 in the chapter dedicated to "Alternative Physics
on Line" in this same volume of Episteme, and so we propose a similar
test, remarking that, at least in principle, this "twin effect" could be
checked also by comparing the time elapsed for a rotating clock
(with constant speed, which makes the formula (24), or (25), applicable,
even if we are not in front of an "inertial" clock) with a reference
clock, which remains still in an Earth's laboratory:
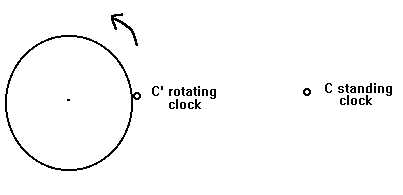
One cannot of course hope to be able to reach very high speeds v of
C' , but one could think to take advantage from the fact that C' could
be rotated for a long period of time. If for instance we take for the radius
R of the rotating platform R = 1 m , and an angular speed w
= 2p
n which is corresponding
to a frequency of n = 50 Hz, then v is just
about 300 m sec-1 , which is almost exactly the Earth's rotation
speed. From the formula (24) we have D
t
= ![]() D
t , which is almost equal (namely, once again, up to second order
in b ) to:
D
t , which is almost equal (namely, once again, up to second order
in b ) to:
(26) D
t ~ (1
- ![]() b
2)
D
t = D t -
b
2)
D
t = D t - ![]() b
2D
t
.
b
2D
t
.
This last equation shows that the rotating clock C' should loose ![]() b
2D
t
sec for each second which is measured by the reference clock C , and since
actually:
b
2D
t
sec for each second which is measured by the reference clock C , and since
actually:
b = ![]() =
= 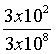 = 10-6 ,
= 10-6 , ![]() b
2
=
b
2
= ![]() 10-12 ,
10-12 ,
then we have that in an hour time the rotating clock should theoretically (according to SR) loose 18 x 10-10 sec , which is about 2 nano-seconds, a value perhaps great enough to be detected (even in the Hafele-Keating test quoted above the "game" is played around a few nano-seconds).
Going on with our pure theoretical (pre-experimental) speculations, what could we expect, from a qualitative point of view, from such an experiment?
Well, according to SR, one should observe not only the expected time retardation, but even that all kind of clocks should show exactly the same slowing down. From an aether-theoretical point of view, instead, a time retardation is not strictly necessary; moreover, if there is one, then it should be explained by some "absolute" effect, namely a real physical effect due to the interaction of the moving clock with the aether. Along this path of thought, a Cartesian physicist should expect that different clocks (atomic, mechanical, etc.) could experience different time dilations (and, why not?, even contractions), at different rates.
The author can hear "orthodox" physicists saying: "this experiment has
to do with one of the phenomena which we observe every day in our particle
accelerators", but we object that the increasing of the mean-life of a
particle (and let us even accept that the corresponding rate is exactly
the one predicted by SR, and moreover equal for all particles) is
not exactly the same thing proposed before. As an example of a physical
cause (coherent with the hypothesis of a dragging aether) which one could
think of, in order to explain the increasing of this mean-life, let us
give the following one, which comes from an analogy (analogies are
methodologically fundamental in Cartesian philosophy). Let us imagine an
ordinary cartesian orthogonal reference frame, with an origin O and three
axes Ox, Oy, Oz , and a rain falling down along z-axis with intensity s
(for instance millimeters of rain for time unity: so s has the physical
dimension of a speed). This means that, if we take a container (a
tea-cup!) in form of a paralleliped (suppose that it has a vertex in the
origin, and the three sides coming out from this vertex along the three
axes of the given reference frame being such that the length along x-axis
is L , along y-axis L' , along z-axis L'' ; so the volume is V = LL'L''
), then, after a period of time T , we will find a volume of water inside
the container which is equal to LL'sT . Suppose now to rotate the cup along
the y-axis of an angle q , less than 90°,
and then ask the same question: what will be the volume of water inside
the cup after a time T ? It is clear that the answer will be LL'sTcos(q
) , and so far so good. Suppose now that the cup - with sides parallel
to the three axes - is moving along x-axis with a velocity v = (v,0,0)
, and then ask once again the same question: after the same time T , what
will be the volume of water inside the cup? It is rather clear that, from
the point of view of an observer moving with the cup at the same velocity
v
, the rain will not fall anymore along the perpendicular to the "base"
of the cup, since one must take in account a kind of "composition of velocities"
(classical aberration, see next section!), and that the rain will fall
for him along the direction (v,0,s) , "aberrated" of an angle q
, with respect to z-axis, such that: cos(q )
= 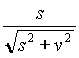 .
.
This obviously means that the case we are studying now is exactly the same as before, as if the cup was simply rotated along y-axis of the same angle q , and then the answer will be once again:
LL'sTcos(q ) = LL'T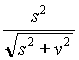 = LL'T
= LL'T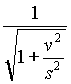 .
.
When comparing this value with the value LL'sT found at the beginning, we find, as it was obvious to expect, that the water inside the moving cup is less than the water inside the standing cup, and, pushing further our analogy, if T = U/LL's is the time required for getting a given volume U of water in the standing cup, then this same time will be equal to:
(27) T(v) = ![]()
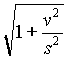 = T
= T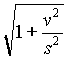
in the case of a moving cup, a time which is bigger than T .
Of course, we claim that we could possibly be in front of a "similar" phenomenon in the case we wished to "explain". Let us call T the mean-life, for instance of a muon, in a terrestrial laboratory: then this T will be, presumably, a function of the given particle and of its interaction with the "surrounding aether". Then we know that a speedy particle will appear to have, from the point of view of the terrestrial laboratory, a bigger mean-life, equal to:
(28) T(v) = g T = 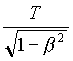 ~ T(1+
~ T(1+![]() b
2)
(up to second order in b ),
b
2)
(up to second order in b ),
which is the value predicted by SR, and which we admit agrees with the experimented value. But let us now compare (28) and (26), by putting in the first equation, as it would be quite "natural", s = c . Then, up to second order in b , the two equations appear to be identical! In conclusion, could we be quite sure that the "true" physical reason of the discussed phenomenon is not of the kind of the "moving cup" model, at least in absence of any evidence of symmetry, which would be essential for the relativistic explanation?
Coming back to the argument of different clocks, and in view of the
possible objection of relativity's supporters (if the proposed experiment
would fail their expectations), that the "failing" clocks are not "good"
ones, the question which must receive a clear answer is: but which is
a "good" clock for SR? (remember that at Einstein's times atomic clocks
were not available, not even in theoretical speculations). As a matter
of fact, the answer is not difficult, since the only one clock which is
good for relativity is the light-clock, which is described in the
following figure (which we take, with the description below, from Marinov's
book: Classical Physics, Part III, High-Velocity Mechanics, 1981,
p. 7):
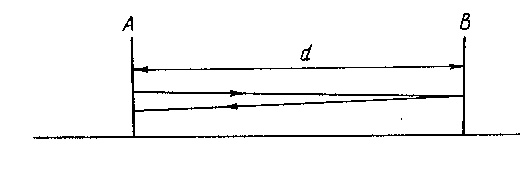
A short light pulse (i.e., a group of photons) is generated at a given initial moment. The pulse flies ... to mirror B, ... it returns to A, where it puts a counter ... showing the number "1" and generates (after amplification) a second pulse which flies to mirror B again; after the return of the second pulse the counter will show the number "2"...
It is rather clear why this the ideal, perfect clock in
SR, and it is curious to remark42 that even from an aether-theoretical
point of view a light-clock would experience some time dilation when in
(absolute) motion through the aether. If we suppose that the absolute velocity
is (v,0,0) along the horizontal arm of the clock43 (say that
its length is L , in such a way that the period of the clock44
is T = ![]() ), then the moving
period would be:
), then the moving
period would be:
(29) T(v) = ![]() +
+ ![]() =
= 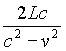 =
= 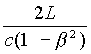 = T
= T  ,
,
which implies that, if one measures some time interval D
t as N = ![]() ticks
with respect to an aether-rest light-clock, then the same time interval
will be measured with N' ticks with respect to the (absolutely) moving
light-clock, in such a way that:
ticks
with respect to an aether-rest light-clock, then the same time interval
will be measured with N' ticks with respect to the (absolutely) moving
light-clock, in such a way that:
(30) N' = ![]() = N (1 -
b
2)
.
= N (1 -
b
2)
.
The previous formula can be interpreted as a time dilation effect due
to the absolute velocity v , and when compared with (26) one realizes that
only a factor ![]() is missing
(of course, the same is true for (29) and (28)). If one introduces a "real"
length contraction too, again due to a possible interaction with the aether,
then one would get exactly the same factor of the relativistic time
dilation. But since we do not have enough information whether this length
contraction must be conjectured or not (see in this same Episteme's
volume the first Larson's paper), we prefer to leave (30) as it is, because
it gives, after all, an instructive example of other possible time
dilations factors, not necessarily equal to the unique one predicted
by SR. In other words, if for instance from an aether-theoretical point
of view, the previous tea-cup model would be able to predict a time dilation
for moving atomic clocks equal to the relativistic time dilation, for light-clocks
this dilation could be different, and so on, so on...
is missing
(of course, the same is true for (29) and (28)). If one introduces a "real"
length contraction too, again due to a possible interaction with the aether,
then one would get exactly the same factor of the relativistic time
dilation. But since we do not have enough information whether this length
contraction must be conjectured or not (see in this same Episteme's
volume the first Larson's paper), we prefer to leave (30) as it is, because
it gives, after all, an instructive example of other possible time
dilations factors, not necessarily equal to the unique one predicted
by SR. In other words, if for instance from an aether-theoretical point
of view, the previous tea-cup model would be able to predict a time dilation
for moving atomic clocks equal to the relativistic time dilation, for light-clocks
this dilation could be different, and so on, so on...
In conclusion, let us repeat it, even if it was true - at least in some measure - that absolute speed effects are such that to imply a perfect quantitative identity with SR predictions, then all the same this would not mean that we are in front of identical physical theories (or of equivalent physical theories, as many physicists like to say), since the proper time should be interpreted, from the point of view of the aether physics, only as an apparent time, while the true time would always be only the coordinate time measured in an (absolute) aether-frame45.
4 - On Relativistic Light's Aberration
We end this paper by proposing at last an optical experiment, but not a test like the usual ones, aimed to measure speeds, or speeds' differences. Rather, we feel that a very important consequence of relativity is the so-called light's aberration, which could easily been explained as follows.
Think, in a coordinate system K of Minkowski space-time as above, of
a photon emitted at the time t = 0 along the y-axis by a light source S
standing still in K , say for instance at the point (0,L,0) . Then, at
the time ![]() , the photon
will arrive in the spatial "origin" of K , the point (0,0,0) . Suppose
instead that the source is moving with respect to K with some velocity
v
= (v,0,0) , and suppose to introduce a proper system K'(x',y',z',t') comoving
with S (with spatial axes "parallel" to x, y and z). Then the photon will
go along a straight line in K' , but not in K , which implies that, at
the time g
, the photon
will arrive in the spatial "origin" of K , the point (0,0,0) . Suppose
instead that the source is moving with respect to K with some velocity
v
= (v,0,0) , and suppose to introduce a proper system K'(x',y',z',t') comoving
with S (with spatial axes "parallel" to x, y and z). Then the photon will
go along a straight line in K' , but not in K , which implies that, at
the time g![]() (now it appears, as it must in SR, the time dilation factor!), the
photon will meet the x-axis in the point (b
g
L,0,0) , and not in the point (0,0,0) as before.
(now it appears, as it must in SR, the time dilation factor!), the
photon will meet the x-axis in the point (b
g
L,0,0) , and not in the point (0,0,0) as before.
So, the aberration angle q is given (in K ) by:
(31) tg(q ) = ![]() = b
g ,
= b
g ,
or even, up to second order in b :
(32) tg(q ) ~ b
= ![]() ,
,
which is the classical formula for astronomical aberration46.
A few mathematics would perhaps describe better the situation.
Motion's equations of the photon in K , when the source is still in K :
x = 0 , y = L - ct , z = 0 ; 3-velocity of the photon in K (0,-c,0) ; speed = c .
Motion's equations of the photon in K' , source moving in K :
x' = 0 , y = L - ct' , z' = 0 ; 3-velocity of the photon in K' (0,-c,0) ; speed = c .
Motion's equations of the photon in K , source moving in K :
x' = x - vt = 0 , y = L - c(t - g![]() )
, z = 0
)
, z = 0
x = vt , y = L - g ct + b
g
vt = L - g ct(1 - b
2)
= L - ct![]() , z = 0
, z = 0
arrival of the photon at y = 0 : L - ct![]() = 0 , t = g
= 0 , t = g![]()
3-velocity of the photon in K : (v,-c![]() ,0)
; speed2 = v2 + c2(1 - b
2)
= c2 .
,0)
; speed2 = v2 + c2(1 - b
2)
= c2 .
This relativistic analysis of aberration shows that, if it is true, according to SR, that the light's speed c does not depend from the source's motion (in our case from v ), then the light's vector velocity can depend from v . As a matter of fact, in the 3-velocity (in K ) of the photon the quantity v does appear explicitely, even if it disappears in the formula which gives the speed.
Well, from a possibly strict aether-theoretical point of view, when supposing the independence of light's propagation from the "source's movement", we could think that the whole vector velocity would not depend from the source, and not only the speed. That is to say, there is possibly in this point a divergence between aether-grounded previsions and the corresponding relativistic previsions. So, is it possible to compare relativistic predictions with analogous aether-theoretical ones, outside from the realm of astronomical observations? In other words, is it possible to test the relativistic aberration of light in an Earth's laboratory??
We suggest to use a circular platform P like in the following picture:
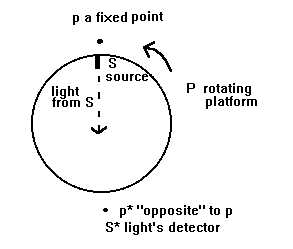
First suppose that P is at rest, and place a mono-directional (the most possible point-like!) photon's source S in the rim of the platform, near to a "fixed" point p in the laboratory. Direct the source towards the centre of P , in such a way that a "fixed" light's detector S* (once again, the most possible point-like), placed near the "antipodal" point p* of p , can detect the arrival of the photons emitted by S . Then, we can make the platform rotate, and arrange things in such a way that, in "stationary" conditions for the angular velocity of P , S does emit photons only when it is in front of p . The goal is to check whether S* will continue to detect these photons, as an aether theory would foresee, or not, as relativity would instead predict. That is to say, one could test whether light is really "dragged" by the velocity of the source, or not.
One could even think to take both detector S* and source S fixed in the laboratory, and to use as a moving source a mirror M (almost possibly point-like, as before!), placed in the rim of P . S does emit photons directed towards the centre A of P , and these photons are reflected only when M passes in front of A (that is to say, with a period equal to 2p R/v = 2p /w - of course, from relativity's point of view, one must specify that this is the period with respect to the laboratory coordinate system). The trace of the backwards photons can be detected by a fixed screen-detector S* .
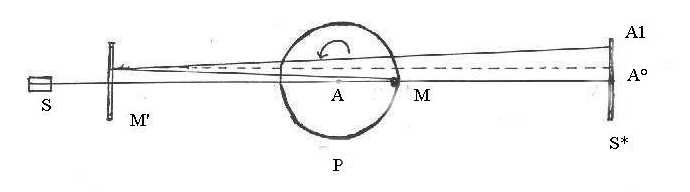
In order to avoid S and S* to be too much close one to the other, one
could think to place a semi-transparent mirror M' at some inessential distance
from S , orthogonal to the photon beam, and at a distance L1
from A , in such a way that the emitted photons can pass through M' . One
could then place S* at some distance L2 from A , in order to
detect the backwards photons reflected by the "other" face of M' , like
in the following picture:
One could even think to increase the expected effect by repeated reflections, introducing another "mirror" placed between the platform and the detector S* .
It is easy to give quantitative evaluations for this Gedankenexperiment. For a given radius R , and a given angular speed w , then the distance between the impact point A° of the inwards non-aberrated photons, and the impact point A1 of possibly aberrated backwards photons would be equal, in force of (32), to:
(33) d x = d x' + d x" = (L1+R)tg(q ) + (L1+L2)tg(q ) = (2L1+R+L2)tg(q ) ,
which is almost equal (up to second order in b ) to:
(34) d x ~ (2L1+R+L2)b
= (2L1+R+L2) ![]() .
.
This identity shows, first of all, that the described test would be called to measure a first order effect in b . For 1 meter radius, a distance L1 = L2 equal to 25 meters, an angular speed w once again corresponding to 50 Herz, then, according to SR, one should have a "shifting effect", after just one reflection, of:
76 x 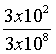 = 76 x 10-6
m ,
= 76 x 10-6
m ,
namely an effect of a few microns, which is perhaps not so small to start with. This effect could afterwards be emphasized - as we have suggested - and finally detected.
It would perhaps be even better, from practical purposes, to replace
the rotating platform with a "very sly" vertical spinning rotor
- as in the following picture - in order to get always an angle of 90°
between the inwards beam, and the reflecting mirror M :

In such a way, the proposed "experiment" would rather be similar to
the famous Fizeau cog-wheel experiment. Summing up, the light emitted
by S is periodically reflected by M . Then, after a new reflection by M'
, the beam hits the mirror-detector S* , from which it is once again reflected
to M' , and so on. If SR is correct, then one should be able to appreciate
an increasing displacement of the trace of the reflected photons,
compared with the original one, corresponding to photons which have not
been reflected (and hence are not aberrated). At the contrary, if the aether-theoretical
prevision is correct, then one should not observe any displacement.
The qualitative side of this last experiment could be perhaps one
of its most attractive features47.
Notes
1 - "Special" refers to the first 1905 Einstein's theory, which did not yet include a treatment of gravitation (Newtonian gravitation was irremiadably out of the requested relativistic "covariance"). After the building of general relativity (GR), we could say that SR is the theory of a flat space-time (a 4-dimensional connected time-oriented Lorentz manifold; in truth, to the property of flatness, one has to add simply connectedness and completeness in order to get the characteristic properties of Minkowski space-time), namely that part of relativity which does neglect gravitational effects due to the presence of the space-time curvature induced by matter. In this sense, SR deals only with electrodynamics in Minkowski's space-time.
2 - One should perhaps emphasize that any "relativistic space-time" in GR, must be be regarded as a purely logical admissible construction, whose only "fault" is that it does not describe the "space" and "time" thought-categories which are rooted in the human mind (a statement this one with which even relativity supporters generally agree). Hence one can just discuss whether these new space-time (or others, there is no limit to abstract mathematical constructions) do correspond in some extent to reality, or not. This remark implies that attempts to prove that relativity is "logically inconsistent" (contradictory in itself) are worst than useless as arguments against relativity (one case for all, the so-called Dingle syllogism, see section 5 in our "Most Common Misunderstandings...", quoted in footnote 18 in the quoted Letter...). This does not exclude, of course, that such attempts could teach, in any case, something interesting (see footnote 14 in that same Letter...).
3 - We say that in the conviction that some of the usual criticism against relativity is, unfortunately, ineffective (see the paper mentioned in the previous footnote).
4 - We must acknowledge that, during his many years of activity, Newton did not always push his criticism against Descartes up to the point to completely refuse the aether. Anyway, what does really matters in this discussion, is the manner in which Newton's ideas have been interpreted - and developed - by his followers, and not which was his original, authentic, thought about this, or others, argument (if there ever was such a "thought", since it could have changed from an age of life to the other, or could have been uncertain, undecided). The historical fact is that the hypothesis of the aether was dismissed after Newton in the conviction that the conception of a "plenum space" was incompatible with the gravitation's law which ruled the the movement of celestial bodies (see also footnote 10), and this is enough for our "judgement". Of course, the two conflicting options influenced the conjectures about the nature of the light too, which was thought of as made up of "corpuscules" in one case, or conceived as a "wave" (perturbation of the medium) in the other (Huyghens).
5 - Which grounds in something like an "antinomy of the pure reason". The conception of an empty space does in fact correspond to the mental space of euclidean-intuitive geometry, the "space" regarded as a "transcendental form" of the human intellect, and it should not by any means be confused with the space of physical reality.
6 - Besides, a rather old argument, expressed for instance almost in the same words by Nicholas of Cusa and Giordano Bruno (traces of its influence can be found even in Copernic). It was at that time needed in order to rebate the objection: "why the pretended Earth's movement around the Sun is not detected by Earth's inhabitants?". This shows that the chief argument which opposes relativity to the aether's physics was already fully active not only at the beginning of XVII Century, but at an earlier date too. As we shall see, the most popular experiments alleged in favour of relativity show only that this pretended movement (the famous aether's wind) cannot be detected in a terrestrial laboratory.
7 - By the way, there were already important studies about the question which gave only to him an unprecedented fame, see Bjerknes' book reviewed in this same volume.
8 - Which - and this could be thought of as a "paradox" - does not include Newton's gravitation's theory itself, since, as it is well known, this was the first victim of the requirement that all physics' laws should be expressed in a covariant form. Of course, people seeing this much beloved theory disappear, together with the "classical" space-time which Newton too used in his work (as everybody else until the beginning of XXth Century!), fall in the mental trap of identifying classical physics with Newtonian physics, and do not realize the importance of the fact that the conception of "physical space" is identical in Newton's and Einstein's approach.
9 - Even the introduction of the term "inertial" (by no means an easy concept to understand: Einstein in fact did not make any attempt of explanation, and just used the language of "ordinary" Newtonian mechanics), show the asserted conservative side of SR.
10 - We feel dutiful a reference to the "unknown" Italian physicist Marco Todeschini, who studied deeply this argument, and advanced the question to investigate Newton's objections to Descartes' "gravitational theory", in order to realize whether they are, at the light of advanced physical and mathematical knowledge, still well-founded or not. See for instance some information about this scientist in: http://www.dipmat.unipg.it/~bartocci/todes.html (in Italian only).
11 - And many other "implicit" assumptions, see footnote 9.
12 - This restriction to inertial observers appears indeed a conceptual weak point of SR, since a fully relativistic approach should perhaps make no difference at all between "states of motion" with respect to nothing (see even the footnote 18 mentioned in the previous footnote 2).
13 - One should not forget that, if Maxwell's theory is "correct" (an assertion, however, which should be investigated with more care: see for instance, both in this same volume, Galeczki's article, or the "Call for papers": Has the last word been said on classical electrodynamics?), then LSP would be a direct consequence of RP, since there is nothing in that theory which connects the speed of an electromagnetic wave to the speed of its source.
14 - Not to say of their "accuracy", either theoretical or instrumental. Flaws appear sometimes unintentional, sometimes more suspicious (see for instance Kelly's paper mentioned in section 3). One of the most interesting examples of this situation, is the analysis of Michelson-Morley's experiment made in: Marco Mamone Capria, Fernanda Pambianco, "On the Michelson-Morley Experiment" (Foundations of Physics, 24, 6, 1994), or the refusal of subsequent Miller's results - obtained during many repetitions of this same experiment - which is discussed in DeMeo's paper listed at the point N. 6 in the chapter dedicated to "Alternative Physics on Line" in this same volume of Episteme. We consider worth of attention under this point of view many papers by the (well known as a critic of relativity) Italian physicist Roberto Monti, in particular his "Theory of Relativity: A Critical Analysis", Physics Essays, Vol. 9, N. 2, 1996, pp. 238-260 (see also his papers published in Episteme N. 3 and N. 4).
15 - The Earth's revolution speed is about 30 km/sec , and it was not detected for instance by Michelson and Morley, Trouton and Noble (see section 2.C), and many others. The Earth's rotation speed in the 24 hours is a more likely candidate for this detection, and it is about 300 m/sec , so an hundred of times less than the previous one, which implies that, for experiments of-second order in b , the factor b 2 = v2/c2 becomes 10.000 times less. We believe that this could be the reason for the experimental "anomalies" pointed out for instance in Van Flandern's paper about GPS (see this same volume of Episteme), but the trouble is that the "detection" of this speed (already realized by Michelson-Gale's experiment, or by variations of Sagnac-kind experiments) would easily be considered uninfluential to our purposes by relativity's supporters, since it does concern non-uniform motions!
16 - See for instance Alessandro Moretti: "L'universo intellegibile, ovvero, la gravità descritta da Leibniz", in Episteme N. 3 (2001) (in Italian only).
17 - One of the very rare exceptions is the experiment
that the Dutch meteorologist Buys-Ballot (1817-1890)  conducted
in order to confirm the Doppler shift. "He put a group of musicians on
a train and took up his position on a station platform. He asked the train
driver to rush past him as fast as he could while the musicians played
and held a constant note, and was able to detect the Doppler shift (as
a change in pitch) as the train passed him (D. Filkin, S. Hawking: Stephen
Hawking's Universe: The Cosmos Explained, BasicBooks, New York:, 1997,
p. 65)". From: http://scienceworld.wolfram.com/physics/DopplerEffect.html
.
conducted
in order to confirm the Doppler shift. "He put a group of musicians on
a train and took up his position on a station platform. He asked the train
driver to rush past him as fast as he could while the musicians played
and held a constant note, and was able to detect the Doppler shift (as
a change in pitch) as the train passed him (D. Filkin, S. Hawking: Stephen
Hawking's Universe: The Cosmos Explained, BasicBooks, New York:, 1997,
p. 65)". From: http://scienceworld.wolfram.com/physics/DopplerEffect.html
.
18 - From the title of the chapter: "Special relativity: Beyond a Shadow of a Doubt", in: Clifford Will, Was Einstein right?, Oxford University Press, 1988 - quoted also in the Letter... which opens this volume.
19 - See for instance Pyenson's book, quoted in the aforesaid Letter... (previous footnote).
20 - We repeat that it seems necessary to accept as a fact the failure of too many experiments aimed to detect an "appreciable" aether's wind in a terrestrial laboratory, and so we confess to have some suspicion towards those people who claim for instance to have proven the existence of an Earth's absolute movement of almost the same amount of the famous speed with respect to the background radiation (and of course these numerical evaluations have been given only a posteriori).
21 - See for instance: Giuseppe Antoni, Umberto Bartocci, "A Simple 'Classical' Interpretation of Fizeau's Experiment", Apeiron, Vol. 8, N. 3, July 2001 (available on line at:
http://www.dipmat.unipg.it/~bartocci/fizhoek.html ).
22 - Robert Resnick, Introduction to Special Relativity, Wiley, New York, 1968.
23 - It is very famous the alleged Hilbert's remark: "Physics is too important to be left to physicists" (see for instance Pyenson's book quoted in footnote 19, p. 183). Unfortunately, from one side it is true that theoretical physics should always be carried on with all the logical exactitude which mathematicians display in their researches. For instance, it is surprising to see how often physicists assert that something cannot be done, giving as only proof the fact that they did not succeed in doing that, when it is well known that any assertion of this kind in mathematics is very difficult to prove (a good example: Paul Cohen's 1963 proof of the independence of the so-called "continuum's hypothesis" from the Zermelo-Fraenkel-Skolem axioms for a set theory; or perhaps, even better known, Galois' proof that it was not possible to give a "general" formula for the solutions of an algebraic equation with degree greater than 4, it would have been certainly not enough to claim this impossibility on the basis that mathematicians did try for some time to find this formula, and that they did not find it!). But from the other side, it is even true that mathematicians have in many recent circumstances shown themselves perhaps worst, with their propensity to aesthetical canons, formalistic abstractness, etc., and that these propensions are one of the not minor causes of the physical "philosophy" we are criticizing (see again Pyenson's book in footnote 19, or, of the present author: "'Cattivi maestri', ovvero, a proposito di un morbus mathematicorum (ma non solo!) recens", at the web page: http://www.dipmat.unipg.it/~bartocci/st/goedel6.htm - in Italian only).
24 - G. Cavalleri, L. Galgani, G. Spavieri, G. Spinelli, "Esperimenti di ottica classica ed etere - Experiments of classical optics and aether", Scientia, Vol. 111, 1976, pp. 667-673.
25 - We should perhaps explicitely remark that in this theory could even happen that observers in effective relative motion could be both in absolute rest, a situation which implies that all aether-frames, or rest-frames, should be considered only as local ones.
26 - "The special theory of relativity grew out of the Maxwell electromagnetic equations. So it came about that even in the derivation of the mechanical concepts and their relations the consideration of those of the electromagnetic field has played an essential role" (A. Einstein, "Elementary Derivation of the equivalence of Mass and Energy", Bulletin of the American Mathematical Society, 41, 1935). See the second Bjerknes' paper in this same volume of Episteme.
27 - "Symmetries and Asymmetries in Classical and Relativistic Electrodynamics", with Marco Mamone Capria, Foundations of Physics, 21, 7, 1991; availabe on line at: http://www.dipmat.unipg.it/~bartocci/symm.html .
28 - Einstein's source was very likely Alfred Föppl's: Einführung in die Maxwell'sche Theorie der Elektricität, 1894, but this case was well known to Maxwell himself (A Treatise on Electricity and Magnetism, 3rd edition, 1892, p. 601).
29 - See for instance: G. Cavalleri, G. Spavieri, G.Spinelli: "On the Action and Reaction Principle in Special Relativity", Nuovo Cimento B, 5, 1988; G. Spavieri: "Proposal for Experiments to Detect the Missing Torque in Special Relativity", Found. of Phys. Lett., 3, 1990.
30 - Some people question whether even Marinov did really perform all the experiments he claimed to have done, or whether they were "professionally" performed, which is perhaps true, at least to some extent. But this could be so only because Marinov, after his exile from Bulgaria, was a poor man, and did everything with his own money and enthusiasm, not having access to public funds, often not used in the best way by luckier establishment's physicists. As far as the strictly experimental situation is concerned, we should perhaps add that Marinov did not use an electric coil, or a magnetic needle, in order to try to detect the torque which was, at last, missing, and that he claims to have used an Hall detector.
31 - The solution below gives the "right" behaviour of fields E and B at infinity, and excludes the so-called advanced potentials as having no possible physical meaning. We could perhaps point out that Roberto Monti (see footnote 14) remarks that in equation (2) it should be added a term s 0E , where s 0 is the possible vacuum conductivity, and that the conventional present-day choice of putting s 0 = 0 is not experimentally so well established as it should be. Even if this observation, in case it was experimentally confirmed, would destroy all pretended covariance of Maxwell's electrodynamics, one must acknowledge that in non-cosmological contexts (such as the ones we shall be dealing with) s 0 seems to be really negligible. In other words, that this would be one of those possible violations of SR on a large scale which would not worry relativity's supporters (see also footnote 11 in the often mentioned Letter...).
32 - See for instance the celebrated Feynman Lectures
on Physics, Addison-Wesley Publ. Co., 1965, "Electromagnetism and Matter".
The author warns (21-5) that it is not so trivial to get (14) and (15)
from (11) and (12), since at first sight "almost everyone" would claim
that after integration it should appear, in the denominator of the fractions,
the retarded distance (namely, the distance from the point in which
the charge is seen at the time t), which is not the case. We could
perhaps emphasize that the distance which appears in (14) and (15), and
the "ordinary" distance ![]() , differ only up to second order in b
, but their difference - which a physicist willing to uncautiously approximate
computations since the beginning, and not only at the end,
would risk to neglect! - is essential to further developments.
, differ only up to second order in b
, but their difference - which a physicist willing to uncautiously approximate
computations since the beginning, and not only at the end,
would risk to neglect! - is essential to further developments.
33 - One should perhaps meditate about the circumstance that this possible factual divergence between classically interpreted and relativistic Maxwell's electrodynamics is in principle meaningful even for a small length of the rod, or for a "low" absolute speed v .
34 - But see also the analysis and the experimental results mentioned in the paper listed at the point N. 17 in the chapter dedicated to "Alternative Physics on Line" in this same volume of Episteme. As far as Trouton-Noble's type experiments is concerned, see also the paper by G. Spavieri, et al., again in this same volume.
35 - In the calculation which leads to formula (20) we did use the fact that F = 0 , and then Ñ F = 0 . This is the so-called Clausius' postulate: "For a circuit in which is flowing a stationary current, the charge density is zero" (another electromagnetic "principle" which is not explicitely stated in ME). Recent reports (for instance: O. Jefimenko, "Demonstration of the Electric Fields of Current-Carrying Conductors", Am. J. of Phys., 30, 1962; T. Ivezic, "The 'relativistic' electric fields produced by steady currents: comparison with experiments", Phys. Lett. A, 156, 1-2, 1991; A.K.T. Assis, W.A. Rodrigues, A.J. Mania, "The Electric Field Outside a Stationary Resistive Wire Carrying a Constant Current", Foundations of Physics, 29, 1999), both experimental and theoretical, have questioned its validity, but this would not change the essence of the present discussion. As a matter of fact, both classical and relativistic Maxwell's electrodynamics should take into account the same modification, and moreover a charge situated right in the centre of a circular circuit should not be affected by the force arising from this nonzero electric potential, apart from "asymmetries" in the circuit (not to say of the fact that the special features of the force (19) could be, at least in principle, allow its detection between other forces).
36 - It is perhaps useful to remark that the charge continuity equation does hold for these classical values of the density charge and of the density current, as well as it does hold for the corresponding relativistic values.
37 - By the way, as one should always expect: mathematics can never give explicitely at the end anything more than it had in itself implicitly, in the original assumptions one started from!
38 - Umberto Bartocci, Marco Mamone Capria, Luigi Mantovani; see Umberto Bartocci: "On a Possible Experimental Discrimination Between Classical and Relativistic Electrodynamics", Proceedings of the International Conference "What Physics for the Next Century?", Ischia, 1991, Ed. Andromeda, Bologna, pp. 88-94.
39 - Umberto Bartocci, Fabio Cardone, Roberto Mignani: "New electromagnetic test of breakdown of local Lorentz invariance: Theory and experimental results", Foundations of Physics, Vol. 14, N. 1, 2001 (see point N. 10 in: http://www.dipmat.unipg.it/~bartocci/listafis.htm, with figures).
40 - Tullio Regge, Cronache dell'Universo , Ed. Boringhieri, Torino, 1981.
41 - This is indeed a popular description of time dilation, but we find it misleading - that is to say, a source for possible misunderstandings - to speak of a "moving clock", since in Minkowski's space-time nothing is really "moving" (space and time are "tied" together, and can be untied only in particular coordinate systems), and so the period of a clock remains always unchanged.
42 - As it is curious to remark that the ideal clock of SR (which, as far as our actual knowledge, has never been realized in practice!) cannot be thought of as point-like, since a length is necessarily required (one could object that any real clock cannot be thought of as point-like, but here the question is different, since the light-clock has even a privileged direction). This shows that, at least in principle, it is not possible to think of a light-clock in an accelerated frame (for instance in the "rotating platform" of Sagnac's experiment: see section 3 in "Most Common Misunderstandings...", quoted in footnote 2), without meeting serious conceptual troubles. This observation refers for instance to the well known difficulties of SR when one wishes to introduce in it some "simple" physical concepts, like for instance the concept of rigid body.
43 - Not fortuitously we have decided to neglect to analyse any "transversal" motion of the light-clock's behaviour from the point of view of an aether theory! It is clear that to discuss this question would be exactly as to discuss the Michelson-Morley experiment, and we have serious doubts about the correctness of its usual theoretical descriptions (see for instance the paper by Mamone Capria and Pambianco quoted in footnote 14). It is obvious that, at least in the case of high absolute speeds, a light-clock should in general simply cease to work.
44 - This period of time is quite suggestive, since it would imply that, thought of a minimum possible length (an hypothesis rather natural in the fluid-dynamical conception of space), call it for instance a metron, then one would have as a consequence a minimum possible time, call it for instance a cronon: 1 cronon = 1 metron / c . Just to give an idea of the possible quantitative size of these units, if we conjecture that a metron has something to do with the so-called Planck length, whose magnitude is about 10-35 m , then the cronon would be about 10-43 sec .
45 - About the supposed equivalence of different physical theories (would the pretended equivalence mean that all possibly conceivable experiments should give the same result? Or that this would be true for only some of them??), it is rather instructive the reading of: Gianfranco Spavieri, "Non-equivalence of Ether Theories and Special Relativity", Physical Review A, 34, 1986.
46 - This light's relativistic aberration was studied by Einstein since his first 1905 paper, since he had to explain the known phenomenon of the annual stellar aberration, discovered by James Bradley in 1728. As a matter of fact, this phenomenon could have thought of, at first sight at least, a physical fact contrary to relativity's principle. We have to admit that Einstein seems to have succeeded in his purpose, and that annual stellar aberration has a good relativistic explanation too - that is to say, one must even admit that this phenomenon has - and it had before Einstein - other "classical" explanations. In truth, this is a rather controversial argument, and are numerous the Einstein's critics which assert instead that SR cannot provide a good explanation for astronomical aberration (see for instance: Thomas E. Phipps Jr., "Relativity and Aberration", Am. J. Phys., 57 (6), June 1989). The point is that, according to SR, only the relative speed between the Earth and the moving star should be the reason for the observed phenomenon, while all stars appear equipped with the same aberration, which does depend only from the Earth's revolution speed v around the Sun. This is of course wholly correct, but the point is that, always according to SR, the phenomenon does depend from a comparison between two positions of the same star in a 6 months interval, when the Earth should be thought of in an (approximatively) inertial frame K' different from the one K in which it was 6 months early ( K' is then moving with respect to K with a speed 2v ). If this argument appears able to "save" SR, at least on this question, and in general, one could object that the indispensable hypothesis for the relativistic explanation of stellar annual aberration is that the relative speed Earth-star does not change significatively in this 6 months time, and that this could not be always the case, for instance when dealing with binary stars, which have a revolution period comparable with that of the Earth, but show the same aberration of all other stars. At this point, relativity's supporters find another ad hoc explanation for these stars, etc., and the question does not appear settled once for all (but see the chapter dedicated to aberration in Reflections on Relativity, http://www.mathpages.com/rr/s2-05/2-05.htm).
47 - For instance one could think to invert the rotation
of the platform, or of the wheel, and to see what happens: that is to say,
whether there is "symmetry" in the observed patterns (the case in favour
of the aether hypothesis), or not (which would be the case in favour of
SR). Needless to say, one should discuss many more practical details
of this "experiment", such as the necessity to provide for a suitable photon
source, since a "real" laser beam is much more similar to a divergent
cone, rather than to a cylinder, as one should instead need
in the actual case. These practical imperfections notwithstanding, a SR
supporter should yet predict that one would truly find an asymmetry
in the trace of the photons in S* , depending on the direction of rotation.
- - - - -
[A presentation of the author can be found in Episteme N. 1]
bartocci@dipmat.unipg.it