Introduzione.

Ci proponiamo nel presente articolo di esporre la deduzione della legge di resistenza al moto dei corpi in un mezzo pulviscolare, basandoci sugli stessi schemi che furono già posti a fondamento di. talune sezioni di un nostro precedente lavoro⁽¹⁾.

Questioni relative alla teoria del moto in un mezzo resistente cominciano nuovamente a suscitare interesse fra gli studiosi che lavorano nel campo della cosmogonia ed in campi affini. Indichiamo ad esempio la serie dei lavori pubblicati dal prof. T. Levi-Civita⁽²⁾, i quali mirano tanto a dedurre la legge razionale di resistenza al moto, quanto a stabilire le equazioni differenziali del moto stesso, ed altresì la serie di studi di G.N. Duboscin (Russ. Astronomical Journal), dedicati principalmente all'analisi generale delle forme e delle proprietà del moto di un punto in un mezzo resistente ed in campi di forze centrali.

Il problema stesso può essere trattato da due punti di vista diversi: come problema di resistenza di un fluido compressibile o no al moto in seno di esso, oppure come problema di resistenza al moto di un mezzo composto di punti discreti, di molecole, l'azione reciproca. delle quali ha importanza e va presa in considerazione solamente per definire la struttura del mezzo nel suo insieme, mentre nell'interrelazione loro col corpo che subisce resistenza al suo moto, dette particelle reagiscono su di esso in modo affatto indipendente l'una dall'altra.

La prima questione, che rappresenta in sostanza un problema di idro od aerodinamica, può presentare interesse per l'astronomia solamente in relazione al moto in mezzi di densità sufficientemente grande, come per es. il passaggio di una meteora attraverso l'atmosfera di un pianeta ecc.

Il secondo problema per altro presenta per la cosmogonia un interesse considerevolmente maggiore, avendo esso da fare con mezzi molto rarefatti. Ed è per l'appunto questo secondo aspetto del problema che prendiamo di mira nel presente lavoro.

§ I. - Espressioni generali per la resistenza nel caso di flusso semplice.

Rappresentiamoci un corpo sferico S , di raggio D intorno al cui centro è descritta una sfera di raggio r , che divide il campo - in cui si può trascurare l'attrazione di questo corpo S - dal campo, interno per rapporto a questa "sfera d'azione", in cui il moto di un punto isolato viene retto unicamente dall'attrazione del corpo S . Rappresentiamo con x₀ il quoziente D/r .

Ammettiamo poi che lo spazio esterno alla sfera d'azione sia, con densità uguale, riempito di particelle materiali tanto piccole per dimensioni e per massa che si possa non tener conto della loro azione reciproca. Sia n il numero di particelle per unità di volume e m la massa di una particella isolata. Supponiamo, che tutte le particelle abbiano masse eguali.

Supponiamo poi che il corpo S si muova rispetto al "centro di moto"⁽³⁾ del complesso di particelle con una velocità r . Esaminiamo, nel paragrafo presente, il caso in cui le particelle non abbiano velocità proprie per rapporto al loro "centro di moto". Questo caso per l'appunto noi chiameremo caso di flusso semplice. Chiameremo asse del flusso la direzione della velocità del corpo per rapporto allo sciame di particelle.

La resistenza che le particelle offriranno al moto del corpo S consterà di due contributi diversi:

1. Resistenza delle particelle che passano attraverso la sfera d'azione senza urtare il corpo S ;

2. Resistenza di particelle urtanti il corpo. L'uno si considererà come assolutamente anelastico.

Applichiamoci a dedurre la formola che corrisponde alle particelle della prima specie.

Indichiamo, come si usa⁽⁴⁾, con a l'angolo fra la velocità di una particella e il raggio vettore nel momento d'entrata nella sfera d'azione; esso sarà anche eguale all'angolo del raggio vettore del punto d'entrata coll'asse del flusso. Siano poi R e N le coordinate polari, per le quali l'asse del flusso serve di asse polare, e finalmente N(r ) l'angolo N corrispondente al punto d'uscita dalla sfera d'azione.

Allora, la proiezione della velocità d'entrata sull'asse del flusso sarà

- r ,

e la proiezione della velocità d'uscita dello stesso punto:

r cos(N(r ) + a ) .

Perciò l'aumento di quantità di moto per il corpo S in direzione dell'asse del flusso in conseguenza dell'incontro con una particella sarà eguale a:

(1) - m r cos²[(N(r ) + a )/2] .

D'altra parte l'equazione della traiettoria di una particella entro la sfera d'azione può essere assunta sotto la forma:

(2) r² r sin2(a ) + (1 - r^2r )sin(a )sin(N) + cos(a )cos(N) - = 0 ,

donde ricaviamo:

(3) [(N(r ) + a )/2] = arctg[(1 - r^2r )tg(a )] .

Così l'espressione (1) si trascrive nel modo seguente:

(1.1) - 2 m r .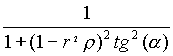

Perciò il completo aumento di quantità di moto del corpo in direzione dell'asse del flusso nell'intervallo di tempo d t provocato dall'incontro con particelle che non vengano ad urtare il corpo stesso sarà:

(4) M d t = - m n 4p r ² d t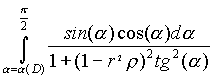

dove a (D) rappresenta il valore limite di a , che corrisponde al. caso in cui la particella viene a contatto col corpo S, cioè:

a (D) = arcsin ,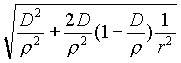

e M la massa del corpo S.

E così, finalmente, per la reazione cercata abbiamo l'espressione

(5) R₁ = M ()₁ =

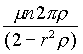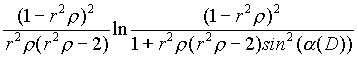= [ - 1 + sin²(a (D))] .

Occupiamoci ora della deduzione della seconda parte della reazione, dovuta all'urto con le particelle per le quali

a < a (D) .

E' facile vedere che se w _R è l'angolo del raggio vettore con la velocità, alla distanza R, e r_R la velocità alla stessa distanza, la componente della quantità di moto di una particella urtante il corpo S nel punto (N,D) lungo l'asse del flusso sarà:

(6) -m r_D cos(N - w _D ) .

Approfittando dell'equazione della traiettoria e della legge delle aree otteniamo:

(6.1) cos(N - w _D ) =

= .

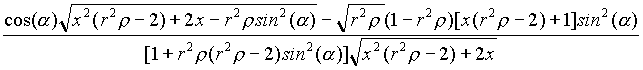Per trovare l'espressione spettante alla variazione di velocità del corpo S nel piccolo intervallo di tempo d t , in conseguenza dell'urto colle particelle del nostro sciame, possiamo procedere nel modo seguente:

Immaginiamoci un certo corpo P* , la cui massa m * sia eguale alla somma delle masse di tutte le particelle, che verranno ad urtarsi col corpo S durante l'intervallo di tempo d t , mentre la componente della quantità di moto rispetto al corpo S sia eguale alla somma delle componenti delle quantità di moto delle particelle medesime, cioè alla somma delle quantità (6). Essendo d t abbastanza piccolo, l'effetto dell'urto con questo corpo fittizio P* e l'effetto dell'urto con lo sciame delle particelle coincideranno fra loro. Così, l'aumento di velocità del corpo S si esprimerà con la formola seguente, derivante dalle legge di urto di corpi assolutamente anelastici:

(7) d r =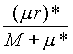

dove M e m * sono rispettivamente le masse dei corpi S e P* e (m r)* la componente delle quantità di moto del corpo P* rispetto a S . La formola (7) rimane naturalmente valida indipendentemente dalle velocità assolute dei corpi in questione, poiché in essa intervengono solo velocità relative.

Abbiamo poi:

(8) (m r)* = -m n 2p r ^{2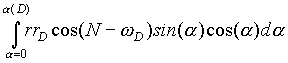 .} d t

e

(9) m * = m n 2p r ^{2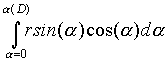 .} d t .

Perciò la reazione cercata sarà in questo caso semplicemente eguale a:

(10) R₂ = M ()₂ = - m n 2p r ² r r_D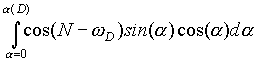

dove a cos(N - w _D) va sostituita la sua espressione (6.1).

Per r_D abbiamo la formola seguente:

(6.2) r_D = .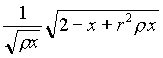

Riassumendo ciò che precede, perveniamo alla conclusione che la forza di resistenza offerta dal nostro mezzo al moto del corpo S sarà rappresentata dalla formola:

(11) R = R₁ + R₂ .

Quest'espressione - particolarmente per il secondo addendo - riesce abbastanza complicata. Non staremo perciò a trascrivere le espressioni complete per il caso generale, ma ci limiteremo all'analisi della legge trovata nelle sue caratteristiche essenziali. E per questo esamineremo in una prossima Nota i casi particolari più importanti.

(1) N. Moisseiev, Ueber einige Grundfragen der lheorie des Ursprungs der Kometen, Meteore und des kosmischen Staubes, I., II., III. Teil, "Publications de l'Institut Astrophysique", vol. V, fasc. I.

(2) T. Levi-Civita, Corpuscoli cosmici e distribuzione Maxwelliana, "Atti Acc. Pontificia", Anno LXXXIII (1930), pp. 176-189; Ancora sul moto di un corpo di massa variabile, questi "Rendiconti", vol. XI, 1930, pp. 626-632; ecc.

(3) Vedi Ueber einige Grundfragen ecc., I. Teil, $ 1.

(4) V. loc. cit.

- - - - -

Questo lavoro, presentato dal Socio Tullio Levi-Civita nella seduta del 3 gennaio 1932, è stato pubblicato nei Rendiconti della Reale Accademia dei Lincei, 1932, Vol. XV, pp. 135-139.