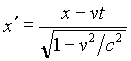
![]()
![]()
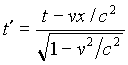 ; (1)
; (1)
(Vladimir Onoochin)
1. Introduction.
In this article, we intend to discuss one point of foundation of the relativistic theory, i.e. the transformational properties of the scalar potential of the uniformly moving charges. The relativistic theory has the pretension to play a role of an absolutely true theory and this fact seems to be undisputable to such extent that some questions laying in the basis of this theory are treated as postulates or as direct consequences of the postulates. However, the special relativity is based on some experimental facts which cannot be derived from the postulates of the theory. The subject of this article is the analysis of the consistency of the relativistic transformations of the potentials with the experimental facts.
Development of the classical electrodynamics at the end of XIX and beginning of XX century went in a way when the main attention was focused on seeking the transformations for the EM field while going from a frame at a rest to the moving frame. However, the expressions for transformed EM fields have not been studied with necessary thoroughness, namely, only the expressions for the fields created by single point charge were analyzed. But even while analysing these simple expressions some points are overlooked; by the way, these points form the basis of the special relativity. We will show that these 'holes' in basement of the special relativity make the latter to be incorrect. We start from well known Lorentz transformations.
It is known from the special relativity that the coordinates in the laboratory frame and uniformly moving frame are connected by the Lorentz transformations:
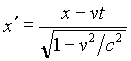
![]()
![]()
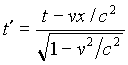 ; (1)
; (1)
and, correspondingly, the charge density and the scalar potential must
transform as:
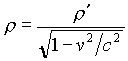 ; (2a)
; (2a)
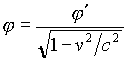 . (2b)
. (2b)
In Eqs. (2), the quantities ![]() and
and ![]() are defined in co-moving frame where the charge is at rest so the quantities
are defined in co-moving frame where the charge is at rest so the quantities ![]() and
and ![]() are equal to zero.
are equal to zero.
If the above equations are fulfilled, then the electrodynamical quantities provide invariance of the physical laws in both inertial frames. We emphasize that, despite of widespread belief, these equations are not postulates1, but they either must be proven or derived from the experimental data.
The first of equations (2) can be easily proven.
Since the charge density of the elementary charge is described by the Dirac
delta function, for uniformly moving charge the proof goes as follows:
![]()
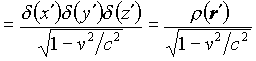 ; (3)
; (3)
which agrees with the law of conservation of the total charge:
 . (4)
. (4)
Validity of Eq. (2b) has been proven by Lorentz who solved the wave equation for the j potential with its rhs describing uniformly moving elementary charge:
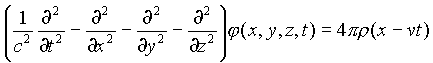 (5)
(5)
in relativistic approach (here, r (x – vt) is the density of the uniformly moving charge).
Finally, we must show that solution of Eq. (5) has the following properties:
- It describes the Liénard-Wiechert and Coulomb potentials of
the uniformly moving charge in co-moving frame and the laboratory frame
respectively.
Before starting the procedure of resolution, it must be noted that the wave equation with the extended source in its rhs cannot be treated as a well defined partial differential equation, because some physics is hidden there. This physics is that one cannot calculate the total potential created by the source as the integral of the potentials created by every moving infinitesimal element of the source. The reason of such a limitation in calculating the sum is that calculating the sum means collecting some information at the only point. But the speed of propagation of information is limited by the speed of light c. So during the process of collection of the whole information about the source, this source displaces itself and actually we cannot determine from what element of the source information comes at a given instant of time.
This problem does not exist in pre-relativistic theories because according to them, the characteristics of the source do not change while going to another frame. But in special relativity all characteristics of the source, except for the value of the charge, do change. Formally we could make some suggestions regarding the changes of the parameters, however, when verifying the foundation of the special relativity, we have to use only quantities which can be measured directly. Taking into account the problem caused by the finiteness of the speed of propagation of information, we conclude that we must use the only way to find the solution in relativistic approach, i.e. we must go to co-moving frame where the source is at rest. In this frame, collecting information from all elements of the source becomes independent on the speed of propagation of information, because the problem reduces to the electrostatic task of finding the j potential created by some extended charge. Then one returns to the original frame so expression for the j potential is transformed too. This expression must describe the j potential in the original frame. We should expect that all transformations during this procedure must satisfy to the requirements of relativistic invariance (covariance). Below we realize this procedure.
According to the arguments given above, we go from
the laboratory frame to the co-moving frame for the charge where the charge
is at rest, so:
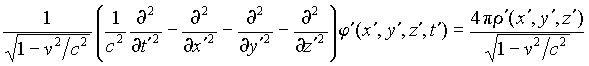 . (6)
. (6)
In opposition to most papers on transformation properties
of the electrodynamical quantities, we keep the factor ![]() in both sides of Eq. (6), in order to show that the wave equations in two
inertial frames differ one from another only by the constant factor.
So the "principle of invariance" is fulfilled for Eqs. (5) and (6).
in both sides of Eq. (6), in order to show that the wave equations in two
inertial frames differ one from another only by the constant factor.
So the "principle of invariance" is fulfilled for Eqs. (5) and (6).
Because the rhs of Eq. (6) does not depend
on the time variable, the lhs should not depend on t' variable
too so this equation reduces to Poisson-like equation (we now omit the
factor ![]() ):
):
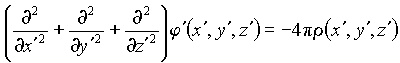 . (7)
. (7)
Solution of Eq. (7) is known. It is the Coulomb potential
created by the charge being at rest:
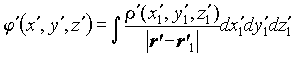 . (8)
. (8)
The final step is to return to the laboratory frame.
By means of Eq. (2b), the scalar potential takes the form:
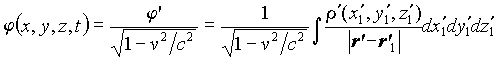 ; (9)
; (9)
where the rhs of Eq. (9) should be expressed via the original
variables ![]() after calculating
the integral.
after calculating
the integral.
But if we analyze the above procedure for the resolution
of the wave equation, we find one strange point. For better understanding,
we write step by step the above procedure in symbolic form. So these steps
from Eq. (5) to Eq. (7) can be written as (we re-write Eqs. (2a) and (2b)
as ![]() and
and ![]() ):
):
![]() ; (10)
; (10)
where W is the operator of the wave equation, sign ![]() means "the Lorentz transformations of the variables (and functions of these
variables)" and sign
means "the Lorentz transformations of the variables (and functions of these
variables)" and sign ![]() means
"which is equivalent to". The second equation in this chain is equivalent
to the third equation, since the "wave operator"
means
"which is equivalent to". The second equation in this chain is equivalent
to the third equation, since the "wave operator" 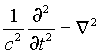 is invariant under the Lorentz transformations, i.e. W' = W
.
is invariant under the Lorentz transformations, i.e. W' = W
.
The inverse procedure, i.e. transformation of the
solution, to the original frame, should be written in symbolic form as:
![]() ; (11)
; (11)
where W-1 is the inverse wave operator. The
chain (11) is correct if the "inverse wave operator" is transformed, under
the inverse Lorentz transformations of the coordinates, as:
![]() . (12)
. (12)
But Eq. (12) is incorrect because the integral operator:
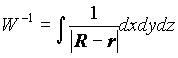 ; (13)
; (13)
is not Lorentz-invariant. So we obtain a strange result, i.e. if one makes inverse Lorentz transformations of Eq. (8), in analogy with the transformations of Eq. (5), one finds that the solution for the j potential via the charge density r does not maintain its original form when transforming from one frame to the other. In different words, despite the form of the wave equation, which is covariant, the solution of this wave equation is not covariant.
The problem can be stated in another way. One is
able to calculate the value of the scalar potential in the laboratory frame
by two methods. First, by treating the rhs of Eq. (8) as some mathematical
expression, one can make the inverse Lorentz transformations of both integrand,
taking into account transformation (2) , and the element of volume dV'
, and then calculate the integral. The second way is to calculate the integral
in the rhs of Eq. (8), i.e. to calculate j
as a function of ![]() , and
then to make inverse Lorentz transformation to the variables
, and
then to make inverse Lorentz transformation to the variables ![]() ,
taking into account that the quantity j transforms
according to Eq. (2b) too.
,
taking into account that the quantity j transforms
according to Eq. (2b) too.
The final results obtained by these two methods are different and this difference is caused by difference in sequence of mathematical operations used while calculating the potential. But because the final result cannot depend on the sequence of mathematical operations (namely, transformation of variables and calculation of the integral), some error must be hidden in the proof of the covariance of the scalar potential.
This difference actually exists. For example, it
is known that the Coulomb potential ![]() cannot
be transformed into the Liénard-Wiechert potential by using the
first method, because, when transforming the charge q', which is
invariant (q' = q), and denominator, one obtains:
cannot
be transformed into the Liénard-Wiechert potential by using the
first method, because, when transforming the charge q', which is
invariant (q' = q), and denominator, one obtains:
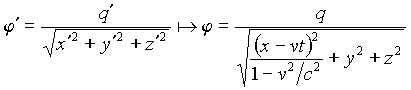 ; (14)
; (14)
and the potential given by Eq. (14) is no the Liénard-Wiechert potential of the uniformly moving charge2.
So, as we have seen above, there is some problem
when trying to prove the covariance of the scalar potential of the single
uniformly moving charge. But Lorentz used another method in proving the
covariance of the j potential3. He
compared the relativistic solution (Eq. (9)) with the solution of the wave
equation (5) obtained by the method of directly solving the wave equation
[3] (Ch. 18.3), and he showed identity of both expressions. Below we analyze
the method of Lorentz, and prove why these expressions are not identical.
3. Direct solution of the wave equation.
In this Chapter, we consider why Lorentz obtained
the relativistic properties for the Liénard-Wiechert and Coulomb
potentials. The solution of Eq. (9), for a charge with spherical shape
in a frame where the charge is at rest, is given by the formula:
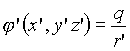 .
(15)
.
(15)
This solution is derived by expansion of the denominator
in a series of spherical harmonic functions (Eq. (3.70) of [1]) in a region
r > r0 , where r0 is effective
radius of the charge. Since the charge has spherical shape, then all terms
of the expansion, except the zero term, are equal to zero, and so we obtain
(15). Inverse transformation of the potential (Eq. (2)) gives:
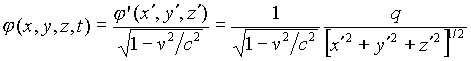 ; (16)
; (16)
and after the Lorentz transformation of the coordinates we have:
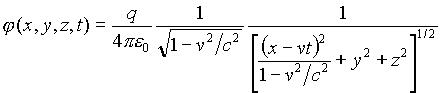 ; (17)
; (17)
or
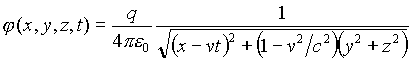 . (18)
. (18)
The above expression is the well known expression
for the LW potential of the uniformly moving charge. Thus, at least in
one case, the relativistic approach gives the correct result, despite of
the breakdown of the Lorentz invariance of the operator (13). Below we
analyze why this is possible. In order to do it, we consider derivation
of Eq. (5) by a method of "direct solution of the wave equations" ([3],
Ch. 18.3). In this method, one does not use Lorentz transformation of the
coordinates, but one introduces some physically reasonable assumptions
while solving the wave equation with the source corresponding to uniformly
moving charge. Obviously, the field created by such a source must follow
this charge. Therefore, the partial spatial and time derivative are not
independent one of another, but they are linked by the relation:
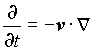 .
(19)
.
(19)
This relation means that any parameter of the field
changes, during the time interval dt, at the same value as while
displacing to the distance –vdt along the direction of motion of
the charge. Taking into account Eq. (19), we are able to transform the
wave equation (5) to:
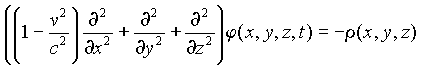 . (20)
. (20)
One can see that dependence of the potential on the
time disappears in the rhs of Eq. (20) so actually Eq. (19) corresponds
to the Galilean transformation of the coordinates:
![]() .
(21)
.
(21)
By change of variables:
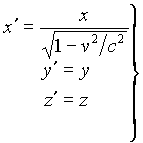 ; (22)
; (22)
Eq. (20) can be reduced to the ordinary electrostatic
Poisson equation:
![]() ; (23)
; (23)
whose solution is:
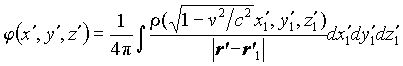 . (24)
. (24)
We have in the lhs of Eq. (24) the scalar
potential in the laboratory frame which, however, is still expressed via
quantities defined in the co-moving frame. Inverse transition is made by
changing the variables:
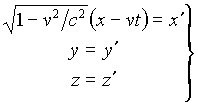 . (25)
. (25)
So finally, we have for the scalar potential in the
laboratory frame two solutions obtained in relativistic approach and by
direct solving the wave equation. For better understanding, we re-write
Eqs. (9) and (24):
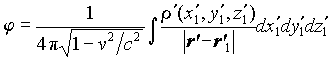 ; (26a)
; (26a)
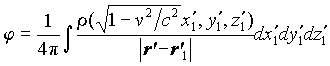 . (26b)
. (26b)
Because both the above equations are written for
the same potential, we must have:
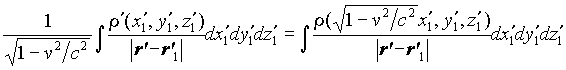 . (27)
. (27)
This will be the basic equation of our further
analysis.
4. Analysis of the function describing the charge density.
This equation can be treated as some integral equation
for the functions ![]() and
and ![]() .
Unfortunately, because these functions belong to different frames we are
not able to compare them4. However, we can get some information
about these functions. Since
.
Unfortunately, because these functions belong to different frames we are
not able to compare them4. However, we can get some information
about these functions. Since ![]() describes a single charge being at rest, it must be represented by some
function with spherical symmetry. By the way, the function
describes a single charge being at rest, it must be represented by some
function with spherical symmetry. By the way, the function ![]() has not such a symmetry5. But in order to satisfy Eq. (27) for
any
has not such a symmetry5. But in order to satisfy Eq. (27) for
any ![]() , i.e. in such
a way that the method of direct solution gives the same results as the
relativistic approach, then it is necessary that the function
, i.e. in such
a way that the method of direct solution gives the same results as the
relativistic approach, then it is necessary that the function ![]() can be transformed to the form which has spherical symmetry. This can be
easily proven by simple consideration. Actually, in order to satisfy Eq.
(27), one can evaluate only the values of the function
can be transformed to the form which has spherical symmetry. This can be
easily proven by simple consideration. Actually, in order to satisfy Eq.
(27), one can evaluate only the values of the function ![]() defined in a limited region of the space, i.e. where the charge
is located. Formally, the function
defined in a limited region of the space, i.e. where the charge
is located. Formally, the function ![]() is defined in the whole space, however, for calculation of the integrals,
only values of this function defined in limited region are essential. In
opposition to this region of internal variables, the region where
is defined in the whole space, however, for calculation of the integrals,
only values of this function defined in limited region are essential. In
opposition to this region of internal variables, the region where ![]() is defined, and it is essential for the calculation of the integral, is
much greater, since it must be the whole space. So the only possibility
to choose the true form of the function
is defined, and it is essential for the calculation of the integral, is
much greater, since it must be the whole space. So the only possibility
to choose the true form of the function ![]() is
to assume that this function can be transformed (in the integrand of Eq.
(27)) into a symmetric one on the variables
is
to assume that this function can be transformed (in the integrand of Eq.
(27)) into a symmetric one on the variables ![]() .
Since when v = 0 the function
.
Since when v = 0 the function ![]() must degenerate into the function having spherical symmetry for the variables
must degenerate into the function having spherical symmetry for the variables ![]() ,
finally we have the functional equation for this function (we omit the
signs "prime"):
,
finally we have the functional equation for this function (we omit the
signs "prime"):
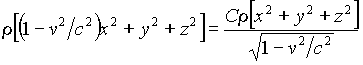 . (28)
. (28)
It can be shown that this functional equation has
two only solutions, i.e.:
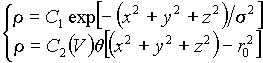 . (29)
. (29)
In the previous formulae C and C1 are some constants, the constant C2(V) does depend on the volume V of the charge, r0 is the radius of the charge, and q is the Heaviside step function. A parameter s in the first solution of (29) corresponds to some "effective radius" of the charge. The second solution in Eq. (29) does describe the model of the electron used by Lorentz, where the charge is represented as a particle with the radius r0 and a uniform charge distribution inside. When this charge moves, its size does contract in the direction of the motion, and, since the volume of the charge contracts too, the value of the charge density arises proportionally. After integration over internal variables, this solution yields Eq. (15).
But it is a well established point in classical electrodynamics [3] (Ch. 18.1) that the only known parameter of the electron is its total charge equal to e, and any calculation of the EM fields and potentials based on some specific charge distribution inside the electron cannot be physically meaningful. So one of the fundamental points of the special relativity, i.e. the proof of the covariance of the scalar potential, is derived by using questionable assumptions. Actually, both charge distributions (29), necessary for the covariance of the scalar potential, are forbidden by quantum mechanics. As a matter of fact, quantum mechanics does not allow the existence of singular distributions (second distribution in Eq. (29) is singular on the boundary of the electron). But the first distribution in Eq. (29) must be caused by some potential of oscillatory type. However, it is not physically sound to suggest that the internal force (Poincaré tension) arises proportionally with the distance (in this case, the internal force would yield the potential of oscillatory type).
We should remark at last that in classical electrodynamics, the elementary charge is described by some singular distribution, i.e. by the Dirac d-function. It is known that this distribution has some representation, and despite the multitude of these representations, the final result cannot depend on the specific representation chosen to describe the elementary charge. However, we have that only the two specific representations (29) do satisfy the condition which is required on the shape of the charge in order that the scalar potential created by the charge of a given shape is relativistically covariant. So the existence of only two specific representations for the d-function, instead of the existence of the whole multiplicity of them, in order to provide for the covariance of the expression for the scalar potential, must be mathematically incorrect.
In conclusion, we obtain that the only relativistically
correct method of establishing the connection between the LW and Coulomb
potentials is relativistically non-invariant itself. Therefore, the relativistic
connection (2b) between these potentials derived by Lorentz looks like
an artefact, which is conditioned by applying the point like approximation
(29b) of the elementary charge. But if we consider the connection between
the LW and Coulomb potentials in a strictly mathematical way, and at very
small distance, we obtain that Eq. (2b) is wrong. Therefore, the scalar
potential cannot be treated as the zero-component of a relativistic four-vector.
Notes
1 Despite of this, in most textbooks on classical electrodynamics, relativistic covariance of the scalar potential is treated as a fact which does not need any proof. For example, in [1] (Ch. 11.9) it is noted that covariance of the vector and scalar potential follows from the covariance (invariance) requirements to all electrodynamical quantities. In [2] (Sec. 16), it is written without any explanations that the vector and scalar potentials form relativistic four-vector.
2 The derivation of the LW potential from the Coulomb potential given in [2] (Sec. 63) is incorrect. Actually, while applying the Lorentz transformation to the lhs of chain (14), it is illegal to change the spatial quantity R' by c(t' - t1'). As a matter of fact, R' = c(t' - t1') is some equation, but not an identity.
3 Actually, Lorentz operated with the fields but not with the potentials, however, the method is the same.
4 It is the main trouble of the special relativity that it is impossible to compare quantities which belong to different frames.
5 This function must describe the charge contracted
in the direction of the motion.
References
[1] - J. D. Jackson, Classical Electrodynamics, 2nd edn (New York: Wiley, 1975).
[2] - L.D. Landau and E.M. Lifshitz, The Classical Theory of Field, (Pergamon, Oxford, 1975).
[3] - W. K. H. Panofsky and M. Phillips, Classical Electricity and
Magnetism, (NY, 1955).
- - - - -
Vladimir Onoochin was born in Gorgii region, Russia, in 1953. In 1990 he took a PhD degree in Physics at Ioffe insititue, St. Petersburg. He is actually the manager of radiophysics (spectrometers) project at Sirius Ltd, Moscow. His main areas of interest are: Electrodynamics of short ultrawideband (UWB) current and EM pulses; Development of the measurement equipment and measurement of the powerful EM pulses in 1 to 150 GHz frequency range; Pulsed power devices. Special points of interest are even some problems in classical electrodynamics usually omitted by mainstream physics, such as penetration of the EM fields through metallic shields, longitudinal EM waves and properties of the EM potentials in different gauges, etc.. To these topics the author has dedicated many research papers.
"Vladimir Onoochin" <a33am@dol.ru>