(Tom Van Flandern)
Abstract. In the GPS, all atomic clocks in all reference
frames (in orbit and on the ground) are set once and stay synchronized.
We can use this same trick to place a GPS-type clock aboard the spacecraft
of a traveling twin. That clock will stay synchronized with Earth clocks,
allowing a clear resolution of the twin's paradox in special relativity
- why the traveler expects to come back younger, and why the stay-at-home
twin is not entitled to the same expectation.
Background
In a previous article [1], I described how the Global Positioning System (GPS) is a marvelous laboratory for testing relativity because the orbiting and ground atomic clocks have differing gravitational potentials and high relative speeds. Their precision is such that the predicted relativistic clock corrections are confirmed to within a fraction of a percent. However, initial expectations based on special relativity were that clocks in different reference frames should have different readings and rates. Yet the Global Positioning System is designed in such a way that, after the individual clock rates are adjusted once pre-launch for the predicted relativity effects, all satellite clocks in all orbits remain in synchronization with one another and with all ground clocks without need for further consideration of relativity corrections, with the exception of one small correction needed for the slight non-circularity of the orbits. The previous article concluded with a discussion of what this means for Einstein's special relativity (SR), and for the competing Lorentzian relativity (LR) theory. The comparison favors LR as the simpler theory describing the relativity of motion.
As history buffs may know, the Lorentz Ether Theory (LET) [2] appeared a year before Einstein's 1905 publication of SR. Of course, LET incorporated both the relativity principle (taken from Poincare, but it was first formulated about a generation earlier) and the Lorentz transformations that bear his name. The essential new element introduced by Einstein the following year was the equivalence of all inertial frames, thereby eliminating the need for the luminiferous ether. This first postulate of SR makes the Lorentz transformations reciprocal; i.e., they work equally well from any inertial frame to any other, then back again; so it has no meaning to ask which of two identical clocks in different frames is ticking slower in any absolute sense. The second postulate of SR makes the speed of light independent of not only the speed of the source (which is also true generally for waves in any medium, including luminiferous ether), but also independent of the speed of the observer (which is a feature unique to SR).
Today, many physicists and students of physics have acquired the impression that these two postulates have been confirmed by observations. However, that is not the case. In fact, none of the eleven independent experiments verifying some aspect of SR [1] is able to verify either postulate. It is now widely believed that no experiment is capable of verifying these postulates even in principle [3], because they become automatically true by convention if one adopts the Einstein clock-synchronization method, and they become just as automatically false if one adopts a different synchronization convention such as the "universal time" postulate of Lorentz. Of interest here is the point that the GPS uses the latter synchronization convention for pragmatic reasons, as I will shortly explain.
So is the difference between SR and LET then purely cosmetic? No, it
is not cosmetic at all. It is true that both SR and LET explain all existing
electromagnetic-based experiments and, in that sense, would remain viable
theories of the relativity of motion. But the difference between them is
much more than aesthetic. In addition to a great difference in practicality
for use in systems such as the GPS (in favor of LET), the two theories
differ about whether or not material bodies can exceed the speed of light
in forward time. In SR, that is proved impossible because time ceases to
advance for any entity traveling at the speed of light. By contrast, in
LR, no speed limit for material bodies exists. It is true that speed relative
to the preferred frame causes electromagnetic-type clocks (which include
all ordinary mechanical, biological, and atomic clocks) to slow, meter
sticks to contract, and the momentum of bodies to be increased by the relativistic
factor ![]() just as in SR.
But in LR, time, space, and the matter content themselves are not affected.
(Here,
just as in SR.
But in LR, time, space, and the matter content themselves are not affected.
(Here, ![]() is the speed of
the body and
is the speed of
the body and ![]() is the speed
of light.) So the question of which theory better represents nature is
of major importance to the future of physics, which is presently invested
in the belief that speeds faster than light in forward time are not possible.
is the speed
of light.) So the question of which theory better represents nature is
of major importance to the future of physics, which is presently invested
in the belief that speeds faster than light in forward time are not possible.
Today, our concepts of the "luminiferous ether" are considerably different than they were in Lorentz's day. It is now widely recognized that the local gravity field serves as the "preferred frame" of LET. With this alteration from Lorentz's original concept but without any change in the math or structure of the theory, LET has now become known simply as "Lorentzian relativity" (LR). Although LR has no intrinsic speed limit, it recognizes the innate difficulty of material bodies composed in part of electrons, while propagating in luminiferous ether, being able to exceed the wave speed of that ether, the speed of light. LR treats this as analogous to a propeller-driven aircraft exceeding the speed of sound without any outside assists, such as from gravity. A force that cannot itself propagate faster than light cannot propel material bodies faster than light.
Of critical importance to choosing the model that best represents nature, none of the eleven independent experiments testing SR verify frame reciprocity or distinguish SR from LR. In fact, historically, de Sitter, Sagnac, Michelson, and Ives concluded from their respective experiments that SR was falsified in favor of the Lorentz theory.1 Indeed, the GPS itself is a practical realization of Lorentz's "universal time", wherein all clocks remain synchronized despite being in many different frames with high relative speeds. However, subsequent re-interpretation of SR allowed that theory to survive these objections.
This "magic" is envisioned to happen by virtue of each clock in the system being synchronized to an imaginary clock in the Earth-centered inertial (ECI) frame, instantaneously co-located with the moving clock, and assumed to be in a gravitational potential equal to that at sea level at Earth's poles. (Note the "coincidence" that the magic makes use of the Lorentzian preferred frame, the local gravity field.) This trick makes the clock rates all the same as they would have been if they were at rest in the ECI frame and in a constant potential field. This is all very nice, but hardly what Einstein envisioned when speaking of two clocks in relative motion, one at a station and one on a passing train. How simple special relativity would have become all these years if physicists had realized that all they had to do was reset the clock rates so they all ticked at the same rate as the reference clock in the local gravity field!
The converse is also true. Suppose we did not change the clock rates before launch, but instead let them tick at their design rates in accord with whatever speed and potential they experienced in orbit. Now, suppose we tried to Einstein-synchronize the system of clocks. Satellite and ground clocks would tick at different rates. And if we tried to work in any local, instantaneously co-moving inertial frame, the corrections needed to synchronize with each orbiting clock would be unique to that observer's frame and different from moment to moment because both clocks are accelerating. The practical difficulties of operating the system would be virtually insurmountable. What we would gain by doing that is constancy of the measured speed of light in all inertial frames. But because all clocks are now re-synchronized to just the ECI frame in the GPS, the speed of light is constant in that one frame, and the invariance of the speed of light in other inertial frames is of no practical value.
In a recent article, Ashby [4] claimed that the clock-epoch correction
term (also called "time slippage" term) in the Lorentz transformations, ![]() (see Eq. below), can be dropped even when its value is large, but he is
very vague about why. However, this particular term is the only difference
of consequence between Einstein synchronization of clocks in different
inertial frames and Lorentz synchronization of clocks to an underlying
"universal time". And the GPS system has been designed to use Lorentz synchronization,
for which one frame, the local gravity field or ECI, is special; not Einstein
synchronization, wherein clocks tick at their natural rates and all inertial
frames are equivalent. By itself, this does not prove LR "right" or SR
"wrong". But the practical difficulties for GPS of not changing the natural
rates of clocks pre-launch, or with the use of SR for any frame but the
Lorentzian preferred frame, are very great. If a ring of satellites (A,
B, C, …, Y, Z) circled the Earth in a common orbit, and each satellite
tried to Einstein synchronize with the next in sequence, then when Z tried
to complete the circuit by Einstein-synchronizing with A, the corrections
required would lead to time readings for A different from the starting
readings, making closure impossible.
(see Eq. below), can be dropped even when its value is large, but he is
very vague about why. However, this particular term is the only difference
of consequence between Einstein synchronization of clocks in different
inertial frames and Lorentz synchronization of clocks to an underlying
"universal time". And the GPS system has been designed to use Lorentz synchronization,
for which one frame, the local gravity field or ECI, is special; not Einstein
synchronization, wherein clocks tick at their natural rates and all inertial
frames are equivalent. By itself, this does not prove LR "right" or SR
"wrong". But the practical difficulties for GPS of not changing the natural
rates of clocks pre-launch, or with the use of SR for any frame but the
Lorentzian preferred frame, are very great. If a ring of satellites (A,
B, C, …, Y, Z) circled the Earth in a common orbit, and each satellite
tried to Einstein synchronize with the next in sequence, then when Z tried
to complete the circuit by Einstein-synchronizing with A, the corrections
required would lead to time readings for A different from the starting
readings, making closure impossible.
Introducing the twins
The "twin's paradox" is an illustration of the complexity of SR's interpretations
of nature. Suppose two identical twins start out at some common instant.
One remains on Earth. The other (the "traveler") is on a spacecraft headed
for Alpha Centauri (AC) four light-years away at 99% of the speed of light,
for which speed the time dilation factor is ![]() .
(We choose a large value of
.
(We choose a large value of ![]() so that the effects of the relativity of motion will be large and obvious,
not subtle.) Upon arrival at AC, the traveler turns back to Earth at the
same speed (or is replaced by a traveler already headed toward Earth of
identical biological age at the moment they pass, to avoid need for an
acceleration). The round trip requires slightly over 8 years Earth time;
let's say 98 months to be specific. This is path 1 in Figure 1. When the
twins are reunited, the Earth-bound twin is 98 months old, and the traveler
is 14 months old (a factor of 7 less).
so that the effects of the relativity of motion will be large and obvious,
not subtle.) Upon arrival at AC, the traveler turns back to Earth at the
same speed (or is replaced by a traveler already headed toward Earth of
identical biological age at the moment they pass, to avoid need for an
acceleration). The round trip requires slightly over 8 years Earth time;
let's say 98 months to be specific. This is path 1 in Figure 1. When the
twins are reunited, the Earth-bound twin is 98 months old, and the traveler
is 14 months old (a factor of 7 less).
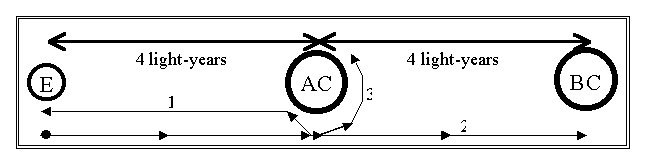
Figure 1.
The traveling twin's journey to Alpha Centauri (AC) begins at Earth
(E).
Upon arrival, the traveler can return to Earth by any path (1),
continue on to Beta Centauri (2), or circle Alpha Centauri (3).
That much is a clear prediction of SR. Note especially that no accelerations
need actually occur at the beginning or end of the journey, nor even in
the middle if we do the "twin replacement" trick. That is consistent with
cyclotron experiments showing that accelerations as such, even as great
as 1019![]() (where
(where ![]() is the acceleration of gravity at sea level), have no effect on clocks
[5]. At each stage of the journey where an event occurs, comparisons can
be made without ambiguity between adjacent points, one in each of the inertial
frames containing the clocks or twins to be compared. Despite the fact
that many textbooks discussing the twin's paradox treat accelerations as
essential, that is illusory. Accelerations are unbounded in size, and in
principle can be done in an instant, allowing no local time to elapse in
any relevant frame. Accelerations (as distinct from velocities) and forces
(as distinct from potentials) do not change local clocks, clock rates,
or biological aging.
is the acceleration of gravity at sea level), have no effect on clocks
[5]. At each stage of the journey where an event occurs, comparisons can
be made without ambiguity between adjacent points, one in each of the inertial
frames containing the clocks or twins to be compared. Despite the fact
that many textbooks discussing the twin's paradox treat accelerations as
essential, that is illusory. Accelerations are unbounded in size, and in
principle can be done in an instant, allowing no local time to elapse in
any relevant frame. Accelerations (as distinct from velocities) and forces
(as distinct from potentials) do not change local clocks, clock rates,
or biological aging.
Now we come to the paradox part: Why isn't the traveler entitled to
claim that the spacecraft remained at rest and the Earth traveled away
at 99% of the speed of light, then turned around and came back? From that
perspective, the original traveler would argue that the Earth-bound twin
should be the younger one. We will examine the rather different answers
to that question offered by SR and by LR.
The traveler takes along a GPS clock
Let's more closely follow what is happening to our two twins. Imagine
that the inertial frame of reference containing Earth and AC is filled
everywhere with synchronized clocks at rest, so that any traveler can always
look out a window and read what time Earth-frame people think it is. See
Figure 2. And let the traveler take a "GPS clock" along on his journey,
along with an unadjusted "normal" clock. The GPS clock is preset in rate
before the journey so that, once placed aboard the spacecraft, it will
remain synchronized in epoch and rate with clocks on Earth, just as real
GPS clocks do. Then the on-board GPS clock will always give readings identical
to the nearest Earth-frame clock visible outside the spacecraft window.
This instant ability to compare traveler's time in his own frame with time
everywhere in the Earth-AC frame will prevent paradoxes from arising.

Figure 2.
From the Earth-frame, all stationary clocks are synchronized,
and all clocks moving with the spacecraft are not. From the spacecraft,
the situation is reciprocal. However, the on-board GPS clock always agrees
with the Earth-frame clock immediately outside the spacecraft window. ©
Now let's examine the journey details. When the traveler's journey begins, the on-board native clock ticks slower than the GPS clock by a factor of seven. But isn't that already an asymmetry present at a stage where there is simply a relative motion, and no way to decide which twin should be aging slower? LR answers simply "yes" because the frame of the local gravity field is the preferred frame in which clocks tick fastest, and time in all other relatively moving frames passes more slowly. But SR offers the opposite answer. And understanding that answer is the key to understanding SR.
SR is a mathematical theory built around the Lorentz transformations.
Let the time ![]() be the reading
on a clock fixed in the Earth frame; and let
be the reading
on a clock fixed in the Earth frame; and let ![]() be the relative location in the Earth frame of a clock fixed in the spacecraft
frame moving at speed
be the relative location in the Earth frame of a clock fixed in the spacecraft
frame moving at speed ![]() relative to the Earth frame. Let
relative to the Earth frame. Let ![]() be the time reading on the natural clock in the traveling spacecraft, and
be the time reading on the natural clock in the traveling spacecraft, and ![]() be the relative location of Earth in the spacecraft's frame. In that frame,
Earth passes the spacecraft with a speed
be the relative location of Earth in the spacecraft's frame. In that frame,
Earth passes the spacecraft with a speed ![]() .
As before, the Lorentz time dilation/length contraction parameter is
.
As before, the Lorentz time dilation/length contraction parameter is ![]() ,
having a value of 7 when
,
having a value of 7 when ![]() . So in general, the relation between the Earth-frame clock and the spacecraft-frame
clock is:
. So in general, the relation between the Earth-frame clock and the spacecraft-frame
clock is:
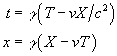 [1]
[1]
Because the relationships are reciprocal (all inertial frames are equivalent
in SR), the inverse relations (with ![]() ) must also hold:
) must also hold:
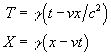 [2]
[2]
Now let's compare time in the two frames. First, let an observer at
a clock fixed on Earth watch time on the spacecraft clock. Then the observer
is looking at a point![]() . Substituting
that into eq. , we get the unsurprising result that
. Substituting
that into eq. , we get the unsurprising result that ![]() ,
meaning that the spacecraft clock remains fixed at the origin of its own
coordinate system. And from the time transformation, using the definition
of
,
meaning that the spacecraft clock remains fixed at the origin of its own
coordinate system. And from the time transformation, using the definition
of ![]() , we get
, we get ![]() ,
which restates the well-known prediction of SR we cited above that the
spacecraft clock will appear to the Earth observer to be ticking
,
which restates the well-known prediction of SR we cited above that the
spacecraft clock will appear to the Earth observer to be ticking ![]() times slower than the Earth-fixed clock.
times slower than the Earth-fixed clock.
That much is routine. But before we leave the Earth frame, let's do
one more calculation. Suppose the spacecraft frame is likewise filled with
clocks everywhere, Einstein-synchronized with each other. Because all such
clocks are at rest relative to one another, they can simply exchange light
signals and assume that the light takes equal time for the uplink and downlink
portions of its round trip. Then the average of the transmission and reception
times on one clock must agree with the signal reflection time on the other
clock by definition of "Einstein synchronization". Now, from the Earth
frame, let's peer into the spacecraft frame at the point ![]() ,
the fixed location of the Earth observer. From Eq. , we now have
,
the fixed location of the Earth observer. From Eq. , we now have ![]() .
The meaning of this relation is that the Earth observer sees a succession
of spacecraft-frame clocks parading by, and time on the succession of clocks
goes by
.
The meaning of this relation is that the Earth observer sees a succession
of spacecraft-frame clocks parading by, and time on the succession of clocks
goes by ![]() times faster
than Earth time.
times faster
than Earth time.
You read that right. According to SR, at the same time that each and
every clock in the spacecraft frame is seen by the Earth frame to tick ![]() times
slower,
time in the spacecraft frame on a succession of passing clocks is passing
by
times
slower,
time in the spacecraft frame on a succession of passing clocks is passing
by ![]() times
faster
than Earth time. To repeat this essential point, in any inertial frame
with a relative motion, all individual clocks tick slower but overall frame
time moves forward at a faster rate. Such is the effect of the
times
faster
than Earth time. To repeat this essential point, in any inertial frame
with a relative motion, all individual clocks tick slower but overall frame
time moves forward at a faster rate. Such is the effect of the ![]() term in the transformation. The time difference between clocks in different
frames is a function of the different rates they tick at and of
the "time slippage" effect, whereby time is a function of location in any
relatively moving frame. In SR, this would remain true even if we used
the GPS trick and eliminated the rate differences between clocks. In general,
the time slippage effect dominates the effect of a changed clock rate for
any clock in a frame with relative motion. (N.B. Time is everywhere the
same when viewed from within an inertial frame. But it is everywhere different
in that same frame from the perspective of any other frame with a relative
motion because of time slippage.)
term in the transformation. The time difference between clocks in different
frames is a function of the different rates they tick at and of
the "time slippage" effect, whereby time is a function of location in any
relatively moving frame. In SR, this would remain true even if we used
the GPS trick and eliminated the rate differences between clocks. In general,
the time slippage effect dominates the effect of a changed clock rate for
any clock in a frame with relative motion. (N.B. Time is everywhere the
same when viewed from within an inertial frame. But it is everywhere different
in that same frame from the perspective of any other frame with a relative
motion because of time slippage.)
It is worth studying the points in the preceding two paragraphs because,
while mathematically permissible, they defy our intuitions and are what
makes relativity such an unintuitive theory.
The traveler looks back at the Earth twin
Now let's switch to the spacecraft frame and look back at the Earth-frame
clock at ![]() using Eq. . Then
we get
using Eq. . Then
we get ![]() and
and ![]() .
So the spacecraft clock sees the Earth clock ticking
.
So the spacecraft clock sees the Earth clock ticking ![]() times
slower than itself. Substituting
times
slower than itself. Substituting![]() ,
we get
,
we get ![]() : the spacecraft
twin sees Earth-frame clocks streaming by outside his window with time
elapsing on a succession of them at
: the spacecraft
twin sees Earth-frame clocks streaming by outside his window with time
elapsing on a succession of them at ![]() time
faster. So both effects, relative clock rates and frame time from time
slippage, are reciprocal and symmetric between the two frames.
time
faster. So both effects, relative clock rates and frame time from time
slippage, are reciprocal and symmetric between the two frames.
And that is SR's answer to the symmetry challenge we posed at the outset of the spacecraft's journey. Both LR and SR predict that the spacecraft's clocks will appear to tick slower than all Earth-frame clocks as viewed by Earth-frame observers. But SR (only) predicts that the situation looks reciprocal and symmetric for observers in the spacecraft frame looking at clocks in the Earth frame. The traveler is therefore not surprised by the behavior of the GPS clock on board, which correctly records a combination slower clock rate plus a fast time slippage for the Earth frame, and stays in agreement with the Earth-frame clocks passing by just outside the spacecraft window.
Now consider the traveler's arrival at AC, when the spacecraft turns around or is replaced by a spacecraft heading Earthward at the same speed. Neither the natural clock nor the on-board GPS clock changes rate or reading significantly during the turn-around. However, before the turn-around, the Earth-frame clocks say four years (actually, 49 months) of Earth time have elapsed since the journey began, and the spacecraft natural clock says seven months of spacecraft time have elapsed. But the spacecraft infers that only a single month has elapsed back on Earth because a single clock in another frame is affected only by clock slowing, not time slippage; whereas the spacecraft agrees that 49 total months have elapsed at AC because the journey began with a 48-month time slippage for AC and added one more month during the journey. As usual, time slippage corrections (where applicable) dominate clock readings in other frames.
We now come to the crux of the resolution of the paradox, which seems paradoxical only in SR. The traveler has inferred that only one month has elapsed back on Earth since his journey began, so by spacecraft-frame reckoning, Earth time is just one month later than the actual departure time. For example, if the journey commenced in 2000 January, when the traveler arrives at AC, the on-board GPS clock reads 2004 February; but the traveler infers that Earth clocks still read 2000 February. Because of the finite speed of light, the traveler can see Earth only as it was, not as it is now, and therefore cannot check this inference by direct observation. According to SR, all these clock-reading inferences are not just illusions, but reflect the real, physical time for each frame involved. So at the same time and place that an AC resident infers that Earth time is 2004 February, the spacecraft traveler infers it is 2000 February - a four-year difference; and both are correct for their respective frames.
Then the spacecraft turns around. Nothing changes locally. But inferences about remote time change greatly because of time slippage, which now has the opposite sign. Now the traveler infers that Earth time is 2008 February - four years into the future instead of the past. As a consequence, the traveler will again infer that only one month of Earth time will elapse during the return journey, and all participants agree that Earth time upon the traveler's return will be 2008 March. The traveler arrives back younger (14 months old) than the stay-at-home twin (98 months - over 8 years old). According to LR, this is because the traveler had a high speed relative to the preferred frame, the local gravity field; and there never was any symmetry between the two frames. But according to SR, the elapsed time is a combination of slowed aging and time slippage effects, the latter changing discontinuously when the direction of the traveler changes.2
The Earth twin thinks the traveler should naturally age slower because
his clocks run slower. And the traveler thinks the Earth twin should naturally
age faster because the time slippage effect dominated the slowed aging
effect when that twin turned around. Note that the traveler could have
taken any path whatever as long as the spacecraft speed relative to the
Earth frame remained 0.99 c . Then at every instant along the journey,
the traveler's biological age will be a factor![]() less
than the elapsed time on the on-board GPS clock, which will agree with
the Earth clocks upon return.
less
than the elapsed time on the on-board GPS clock, which will agree with
the Earth clocks upon return.
Indeed, the spacecraft could have simply continued in a straight line past AC and on to Beta Centauri (BC), say (for purposes of this example only), 8 light-years from Earth. Then there was no turn-around event, but the traveler is still just 14 months old on arrival, and twins born on BC at the same time the Earth twin was born (according to Earth-frame clocks) will still be 98 months old. And the traveler will infer that the BC twins started out 96 months old at the journey's beginning, and aged just two months during the journey. So clearly, neither the turn-around event nor any acceleration is essential to the result; and the SR resolution of the paradox retains its symmetry and the equivalence of all frames.
Hence, from the traveler's perspective, wherever the spacecraft goes
in any direction without changing speed relative to the Earth frame, it
will encounter Earth frame clocks with more elapsed time than on
the natural clock aboard the spacecraft (but with the same elapsed time
as for the on-board GPS clock). But the traveler will infer that all clocks
in the Earth frame are always ticking slower than the natural spacecraft
clock, and beings in the Earth frame are always aging more slowly than
the traveler. Everything encountered can be explained by a combination
of clock rate changes and time slippage. The traveler cannot infer that
the Earth-bound twin will be the younger one upon the spacecraft's return
because Earth experienced a time slippage event (whether sudden or gradual),
rapidly aging everyone on Earth during the traveler's journey. That time
slippage event is no different in character than the one that a hypothetical
twin on Beta Centauri would experience if the traveler continued on past
AC without a turn-around event.
The traveler takes different paths
What we have just described are careful and correct inferences of SR as applied to the twin's paradox. This also shows the essentially mathematical nature of the theory, because it does violence to what we fondly call "common sense". The most important point to note carefully is that the theory is internally consistent, and no mathematical contradictions can be found no matter how the transformation equations are manipulated, or how many frames or twins are introduced. The next important point to note is that SR makes demands on our credulity that LR does not. Let's examine why.
At the point of turn-around on the original journey from Earth to AC, the traveler's inferences about time on Earth changed suddenly. Instead of the physically unrealistic instant turn-around, let's assume the spacecraft "orbits" around AC to perform the turn-around. (To stay at a safe distance from the star at the same speed, this would require propulsion, not just gravity.) This can still take a time short enough to be neglected, especially at such a high relative speed. So the traveler's spacecraft changes from headed away from Earth and inferring the Earth year is 2000, to traveling toward Earth and inferring the Earth year is 2008. Again, SR says this is real, physical time, and not an illusion.
So before commencing a journey back to Earth, let's suppose the traveler
orbits AC several times. Then each time the traveler heads away from Earth
in that orbit, Earth time drops back to 2000; and each time the traveler
heads toward Earth, inferred Earth time becomes 2008. The Earth-year is
intermediate for intermediate orbital positions. Now the significance of
repeating this situation several times is that, as Earth time goes to 2008,
many people will have died and others will be born. And on each occasion
that Earth time reverts to 2000, some of the dead will be resurrected and
some living young children in 2008 will cease to exist in 2000. Note that
while all this is happening according to SR, the on-board GPS clock representing
LR's "universal time" continues to insist that Earth time is the same as
spacecraft time and AC time: 2004 everywhere. In SR, effects of this type
are never observable because they "lie outside the observer's light cone",
hidden from direct view by the finite speed of light. Nonetheless, SR insists
that such changes affect real, physical time and are not mere illusions,
because the viewpoint of each inertial frame is just as valid as that from
any other frame.
Conclusions
In LR, one reference frame (the local gravity field) is preferred; and speed cannot affect time, but only the rate of ticking of mechanical, electromagnetic, or biological clocks. However, just as we do not assume that time has been affected when the temperature rises and causes a pendulum clock to slow down, LR says that changes in clock rates are changes in the rates of physical processes, and do not affect space or time. So by carrying an on-board GPS clock on the spacecraft, we are offered a clear choice between models: Earth time can be what SR infers it is, or it can be what the GPS clock says it is. In the former case, SR works, but leads to heavy-duty complexities and fantastic inferences about the nature of time at remote locations. Moreover, the proof that nothing can travel faster than light in forward time stands intact. In the latter case, LR works with great simplicity and in full accord with our intuitions about the universality of the instant "now". And the speed of light is no longer a universal speed limit because time itself is never affected either by motion or by gravity.
Aside from these practical difficulties with the use of SR in the GPS,
Einstein's special relativity is also under challenge in a more serious
way from the "speed of gravity" issue, because the proven existence of
anything propagating faster than light in forward time (as all experiments
indicate is the case for gravity) would falsify SR outright [6, 7]. So
it is entirely possible that reality is Lorentzian, not Einsteinian, with
respect to the relativity of motion. In that case, physics may have no
speed limit when the driving forces are gravitational or electrodynamic
rather than electromagnetic in nature. And that may be the most important
thing that the GPS has helped us to appreciate.
Notes
[1] T. Van Flandern, "What the Global Positioning System tells us about relativity", in Open Questions in Relativistic Physics, F. Selleri, ed., Apeiron, Montreal, 81-90 (1998). Also available on-line at <http://metaresearch.org>, "cosmology" tab, "gravity" sub-tab.
[2] H.A. Lorentz, Lectures on Theoretical Physics, Vol. III, "The principle of relativity for uniform translations", Macmillan & Co., London, 208-211 (1931). Contains summary of and citation to original 1904 paper.
[3] H. Erlichson, "The rod contraction-clock retardation ether theory and the special theory of relativity", AJP 41, 1068-1077 (1973).
[4] N. Ashby, "Relativity and the Global Positioning System", Phys.Today May, 41-47 (2002).
[5] Bailey, J., Borer, K., Combley, F., et al., "Measurements of relativistic time dilation for positive and negative muons in a circular orbit", Nature 268, 301-305 (1997).
[6] T. Van Flandern, "The speed of gravity - What the experiments say", Phys.Lett. A 250, 1-11 (1998).
[7] T. Van Flandern and J.P. Vigier, "Experimental repeal of the speed limit for gravitational, electrodynamic, and quantum field interactions", Found.Phys. 32(#7), 1031-1068 (2002).
1 De Sitter argued that the forward displacement of starlight (aberration) depended on absolute, not relative, speeds because both components of a double star, each with some unique velocity, had the same aberration. Sagnac argued that the fringe shifts expected but not seen in the Michelson-Morley experiment are seen if the experiment is done on a rotating platform. Michelson argued in the 1925 Michelson-Gale experiment that the Earth was just such a rotating platform. Ives argued that ions radiated at frequencies determined by absolute, not relative, motion because they had to pick a specific frequency to radiate at. In each case, a complex-but-now-familiar SR explanation could account for the same observed results.
2 We note in passing that the effect that SR expects accelerations
or frame changes to have on remote clocks would constitute an instantaneous
action at a distance, a violation of the causality principle.
Acknowledgments
The author thanks the Meta Research Board and members for financial support, with a special thanks to Tim Seward. The artwork in Figure 2 is Copyright (2002) by Boris Starosta, <http://starosta.com>.
- - - - -
Tom Van Flandern received his Ph.D. degree in
Astronomy, specializing in celestial mechanics, from Yale University in
1969. He spent 20 years at the U.S. Naval Observatory, where he became
the Chief of the Celestial Mechanics Branch. In 1991, Tom formed a Washington,
DC-based organization, Meta Research, to foster research into ideas not
otherwise supported solely because they conflict with mainstream theories
in Astronomy. Tom is editor of the Meta Research Bulletin, which
specializes in reporting anomalies and evidence that does not fit with
standard theories in the field. During the past few years, he has also
been a Research Associate at the University of Maryland Physics Department
in College Park, MD, and a consultant to the Army Research Laboratory in
Adelphi, MD, working on improving the accuracy of the Global Positioning
System (GPS). North Atlantic Books is the publisher of Tom's 1993 book,
Dark Matter, Missing Planets and New Comets. A second edition was
published in 1999. As with his research papers, the book is critical of
many standard models in astronomy, such as the Oort Cloud, the Dirty Snowball,
and the Big Bang theory. Tom also organizes the Eclipse Edge Expeditions
to optimal solar eclipse viewing sites. During his career as a professional
research astronomer, Tom has been honored by a prize from the Gravity Research
Foundation; served on the Council of American Astronomical Society's Division
on Dynamical Astronomy; taught astronomy at the University of South Florida
and to Navy Department employees; been a consultant to NASA's Jet Propulsion
Lab; and done several spots for the "Project Universe" series that continues
to air occasionally on public TV.
Meta Research <tomvf@metaresearch.org>
http://metaresearch.org/