Physics Essay volume 10, number 1, 1997

Physics advances by the recognition of simple patterns. The simplicity in the pattern is usually evidence of an underlying simplicity in nature. By using the simplest possible underlying model, we are able to understand things more quickly, allowing us to probe to deeper depths of understanding while not requiring us to dwell on the many tedious details of a cumbersome and highly parameterized model.

The present Standard Model^(1–10) for elementary particles and interactions works very well, but there are at present a rather large number of "elementary" particles thought to compose nature. This paper will identify a new simple pattern, which will be shown to dovetail with the Standard Model but which uses far fewer constituents. This single paper cannot, of course, replicate all of the tremendous success of the Standard Model and its thousands of man-years of effort. There are no dynamics presented here - only the exposition of a simple pattern in nature. Despite the lack of dynamics, the numerology alone can be used to make one clear experimental prediction: a 69-GeV Z-like peak in colliding beam experiments should exist if the pattern presented here is representative of nature.

The basis set of particles comprising the Standard Model is usually advertised to consist of six quarks and six leptons. But the advertised basis set represents only a portion of the picture. For every particle in the advertised basis set there is also a corresponding antiparticle. A further complication arises with the Standard Model of strong interactions, which associates one of three colors to each quark and one of three complementary colors to each antiquark. The Standard Model requires any bound state of quarks to be color-neutral. (Anti)Baryons arrange color neutrality by being composed of three (anti)quarks, one (anti)quark for each (complementary) color, while mesons arrange color neutrality by being composed of one quark and one antiquark, with the quark having a specific color and the antiquark having the associated complementary color.

Thus, rather than the simple six quarks and six leptons usually associated with the Standard Model, there are actually six quarks for each of three colors, six antiquarks for each of three complementary colors, six leptons and six antileptons, for a total of 48 "elementary" particles for the Standard Model. It is therefore desirous to look for a simpler model for elementary particle physics, since one would hope nature employs far fewer than 48 elementary particles.

The fact that the three massive leptons are identical in many ways leads one to the speculation that they may be different states of a single entity. One possibility is that the massive leptons are themselves composed of substituent particles. Such a speculation is supported by an analogy to atomic structure. When a muon decays the decay products are

that is, a muon decays into an electron and two neutrinos. In the atomic physics realm it is relevant to note that the 2s state of hydrogen decays via

that is, the 2s state of hydrogen decays into the 1s state of hydrogen and two photons. The hydrogen atom is modelled very well as consisting of two substructure particles, a proton and an electron, bound by a force carried by a photon,

which by analogy leads to the possibility that the leptons consist of two substructure particles A and B, bound by a force carried by a neutrino,

Here L can be any lepton, and the analogy to atomic states suggests that the electron is the 1s state of the system, the muon the 2s state, and the tauon the 3s state. Continuing the atomic analogy, other states of the system are of course possible. But should p states exist, dipole radiation would be allowed. States that can decay via dipole radiation are much shorter-lived than the metastable 2s state. The short lifetime and the associated broad energy resonance would make such states too difficult to detect. Also, if the 3p state exists below the 4s, the 4s would also decay too rapidly for detection. Thus it may be that only the 1s, 2s, and 3s states exist long enough for detection.

While it is known that neutrinos do not interact strongly with matter, it is still possible that they are the carriers of the intranuclear and intraleptonic force. Again appealing to the atomic analogy, it is known that many frequencies of light readily go through substances such as diamond, where the electric charge carriers are in bound energy states far from the continuum, while in metals, where the energy states are nearly a continuum, electrons readily scatter light. If the neutrinos bind substituents very strongly, the bound state energy will be very far removed from neighboring energy states, and very little interaction between neutrinos and matter is expected.

The binding energy associated with an interaction is related to the coupling constant. For the neutrino to carry the force responsible for binding preons into leptons and hadrons, which involves a binding energy in the giga-electron-volt range, this coupling constant must be large in comparison to the coupling between the photon and the electric charge. But there is no reason why such a strong coupling cannot exist.

Measurements to date have not found any substructure of leptons, but the probes used to detect substructure look for electrodynamic coupling to the purported components. If one of the substructure particles carries no electric charge, no such substructure will be indicated. Therefore, if we assign A as the chargeless substituent, and realizing that the neutrino carries no electric charge, we see that the charge carried by B must equal the charge carried by the lepton, -1:

A = A⁰; B = B^-1. (5)

it is equally true that the same family can be constructed in the this way,

provided we assign electric charge as

C = C⁺²; D = D^-1; E = E⁰. (8)

[Both Eqs. (6) and (7) have an ad hoc origin. They are axiomatic proposals to be tested.]

p⁺¹ = C⁺²-E⁰-E⁰-D^-1; n⁰ = C⁺²-E⁰-D^-1-D^-1. (9)

Equation (11) allows the process of beta decay to be understood as a process whereby a B^-1 undergoes a quantum tunnelling to escape from its potential well within the neutron. This virtually free B^-1 can then react with particles that are pair-produced from a vacuum:

n⁰ = (C⁺²A⁰B^-1B^-1)

It is well known that a vast array of particle physics can be easily modelled using quarks as the substituents of matter. It is possible to recover the quark model from the model proposed herein if another analogy with atomic physics is made. In the lithium atom there exists (we believe) a nucleus of electric charge (e-charge) +3 and three electrons each of e-charge -1. In the ground state two of these electrons are in the 1s state, and the remaining electron is in the 2s state. If one of the 1s electrons is promoted to the 2s state, the lithium atom will acquire a new energy and therefore a new mass. If the 2s electron is promoted to the 3s state, the lithium atom will acquire another mass. By analogy, C⁺² should be assigned a neutrinic charge (n-charge) of +3, the A⁰ an n-charge of -1, and the B^-1 an n-charge of -1. The analogy between baryons and the lithium atom breaks down a bit when it comes to assigning quantum state levels to the system, since in the case of baryons the A⁰ and B^-1 are not identical particles (they have different e-charge), and they may be bosons, whereas in the lithium atom all electrons are identical fermions. Therefore, it is possible in the baryons for all the substituents to be in 1s states for the ground state of the system. When a substituent B^-1 is in a 1s state, the baryon will have its lowest energy. Promotion of the substituent B^-1 to the 2s state will result in a baryon with greater mass, but otherwise identical to the original. Promotion of the substituent B^-1 to a still higher excited state will result in an even higher mass of the baryon. This picture is entirely consistent with the present quark picture if we label the baryon with a d quark when a B^-1 is in the 1s state, label the baryon with an s quark when a B^-1 is in the 2s state, and label the baryon with a b quark when a B^-1 is in the third state.

Similarly, if an A⁰ is in the 1s state, it is equivalent to a baryon that is labelled with a u quark, if an A⁰ is in the 2s state, it is equivalent to a baryon that is labelled with a c quark, and if an A⁰ is in the third state, it is equivalent to a baryon that is labelled with a t quark. However, if the 2p state for the A system lies below the 3s, there will be no sufficiently long-lived t quark to observe.

Generally, for every particle that exists in nature an antiparticle also exists with equal and opposite quantum numbers. Thus six particles are proposed here to compose all matter and antimatter:

The elementary particles:

e-charge (quantum number of electric charge) 0 -1 +2

n-charge (quantum number of neutrinic charge) -1 -1 +3

Estimated mass (GeV/c²) 45.5 34.5 69.0

In Eq. (13), and for the remainder of this paper, I will use the convention that the n-charge is a superscript preceding the indicative letter, and the e-charge is a superscript anteceding the indicative letter. The leptons and antileptons are then the zero total n-charge composite particles possible without a C substituent:

(14)

In Eq. (14) it is recalled from Eq. (4) that the force holding the massive leptons together, now realized as the neutrino-motive force, is carried by the neutrino, and further, that it is assumed that a quantum of the force carrier (one neutrino) is bound within the massive leptons. [Again, the (anti)electron is presumed to be the ground state of the system proposed in Eq. (14), the (anti)muon the first excited state, and the (anti)tauon the second excited state.]

With the same n-charge responsible for holding together the hadrons, and including a bound neutrino for each of the three binding relationships within the baryons, the baryons and antibaryons are the zero total n-charge composite particles containing one C:

(15)

In Eq. (15) any ^-1Y^e is either a ^-1B^-1 or an ^-1A⁰, dependent upon the baryon of choice, and any ⁺¹X^e is either a ⁺¹B⁺¹ or an ⁺¹A⁰, dependent upon the antibaryon of choice. If the (anti)baryon contains an (anti)down quark, this is equivalent to the (⁺¹X^e)^-1Y^e in the (anti)baryon being a (⁺¹B⁺¹)^-1B^-1 in the ground state. If the (anti)baryon contains an (anti)strange quark, a (⁺¹X^e)^-1Y^e in the (anti)baryon is a (⁺¹B⁺¹)^-1B^-1 in the first excited state. If the (anti)baryon contains an (anti)bottom quark, a (⁺¹X^e)^-1Y^e in the (anti)baryon is a (⁺¹B⁺¹)^-1B^-1 in the second excited state. If the (anti)baryon contains an (anti)up quark, a (⁺¹X^e)^-1Y^e in the (anti)baryon is an (⁺¹A⁰)^-1A⁰ in the ground state. (Anti)charm quarks correspond to an (⁺¹A⁰)^-1A⁰ in the first excited state.

There are two more simple ways to make composite particles having zero total n-charge. The first way is through binding of particles with antiparticles:

Particle–antiparticle:

the other is through a combination which includes two C’s, recognizable as mesons:

Mesons of a particular quark flavor correspond to the ^-1Y^e or ⁺¹X^e being a B or A in a ground or excited state in the same way as in baryons.

In Eqs. (16) and (17) the number of neutrinos used in the bonding corresponds to the number of n-charges neutralized by the bonding. Note that since baryons and leptons contain an odd number of neutrinos, they are fermions (spin n/2 with n an odd integer), and that since mesons contain an even number of neutrinos they are bosons, in agreement with experiment. (All particles contain an even number of A-B-C particles, so the A, B, and Cs may either be all fermions or all baryons.)

Next, the topic of colliding beam physics must be addressed. In the case of proton–antiproton colliders we have p⁺¹ + p^-1 ® stuff, or

At appropriate collision energies single pairs of A’s, B’s, and C’s can be resonantly produced. Producing a B pair would require annihilation of the C’s, A’s, and two neutrino–antineutrino pairs, and since many annihilations are required, it is likely that the cross section for this annihilation will be low. In any event, hadron colliders typically operate at center-of-mass energy well above that necessary for resonant production. At these higher energies a multitude of other reactions is possible.

For instance, it is possible that a hard collision might knock a ^-1A⁰ off a proton and a ⁺¹B⁺¹ off an antiproton. The rest of the proton and antiproton would go into a hadronic shower. The antineutrino of a vacuum-produced neutrino–antineutrino pair would combine with the ^-1A⁰ and ⁺¹B⁺¹ to produce a positron, with the remaining neutrino of the pair indicating a "missing" energy upon event detection. It is just such a signature that has been identified with the detection of the W in hadron colliders. The center-of-mass energy for this event, under the model proposed here, is M_Bc² + M_Ac², where M_Bc² and M_Ac² are the rest mass energies of the B and A, respectively. From experimental data, then,⁽¹¹⁾

M_Bc² + M_Ac² = 80 GeV. (19)

(Note that particles of large rest mass, the A’s, B’s, and C’s, combine to form particles with very low rest mass, the hadrons and leptons. This implies that the binding energies of the composites are on the order of the rest mass energies of the sum of the constituents.)

2M_Ac² = 91 GeV Þ M_Ac² = 45.5 GeV. (20)

Using Eq. (19),

M_Bc² = 80 GeV - M_Ac² = 34.5 GeV. (21)

Therefore, the model proposed here predicts that a signature should be observed as the result of B pair formation at an energy of 2M_Bc² = 69 GeV. The signature should be very similar to that observed at 91 GeV for A pair production.

If the probability for knocking an A off a proton during a collision is P_A(E) (which is energy-dependent), and the probability for knocking an A off an antiproton is also P_A(E), the probability for A pair production is

P_AA(E) = P_A(E)P_A(E) = [P_A(E)]². (22)

Similarly, the probability for B pair production is

P_BB(E) = P_B(E)P_B(E) = [P_B(E)]². (23)

The simplest guess of the production probabilities for A’s and B’s is P_A(E) = 2P_B(E), since there are twice as many A’s in a proton (antiproton) as B’s. In that case, the strength of the 69-GeV signal should be 1/4 of that seen at 91 GeV. The lack of observation of a 69-GeV "Z-like" signal must be admitted as being contraindicative of the model proposed herein. However, it is possible that P_BB(E)/P_AA(E) is in actuality low enough that the 69-GeV signal is either lost in the background or is small enough that it has escaped detection up to now. The estimated 1/4 signal strength is only a very naive guess based on an assumption that it is equally likely for a B to be knocked out of an (anti)proton as it is for an A. But the B is different than the A. It has a different mass and possesses e-charge. The excited states of the B are bound to the C more tightly than are the A counterparts, as is evidenced by the lower mass of the down family of quarks. So it may be harder to knock out a B. Nonetheless, some signal at 69 GeV is expected.

For electron–positron colliders we have e⁺¹ + e^-1 ® stuff, or

One of the "great successes" of the Standard Model is the prediction of R, the ratio of hadron production to muon production in electron–positron colliders. Via the Standard Model, R is proposed to be given by

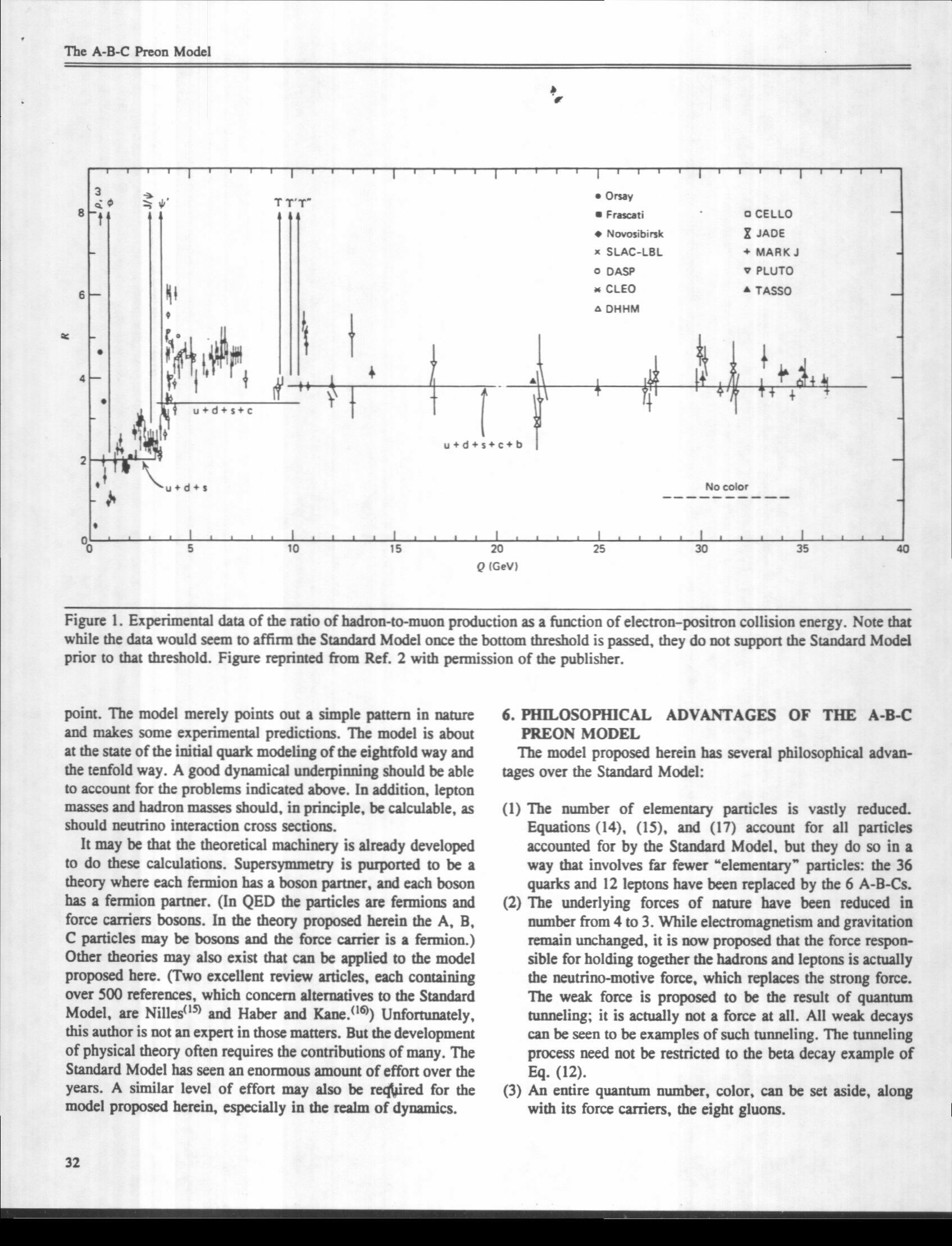
But when one looks at the R data, the Standard Model is not that definitive. Figure 1 shows the experimental data as they relate to hadron and muon production.⁽¹³⁾ While the data do fit the Standard Model prediction for energies above bottom production, they do not fit well for energies between charm production and bottom production. By the Standard Model R should go up once bottom production is allowed, experimentally R goes down. To make a claim that the R data prove that the Standard Model is correct and that therefore color exists is a big stretch of the experimental realities.

3. Deep Inelastic Scattering

Use of deep inelastic scattering data can be used to arrive at an estimate for the mass of the C particle. If we assign M_Cc² = 2M_Bc² = 69 GeV and assume that the momentum fraction carried by a parton is proportional to its mass, the proton's massive partons, the C, B, and 2 A’s, carry 35%, 18%, and 47% of the proton momentum, respectively. [M_Cc²/(M_Cc² + M_Bc² + 2M_Ac²) = 35%, etc.] The quark model predicts that about 35% of the momentum is carried by u partons, 18% by d partons, and 47% by uncharged (gluon) partons, where the u parton has -2 times the electric charge of the d. In the model proposed herein the C has -2 times the e-charge of the B, and the A’s are uncharged. Therefore, both the quark model and the model proposed herein predict that the positive partons will carry 35% of the momentum, the negative partons 18%, and the neutral partons 47%, in full agreement with experiment.

The model presented here leads to some predictions for future results in high-energy physics experiments. First, "neutrino oscillations" should be seen at some level. For the model proposed here to be as simple as possible, once helicity is accounted for, all neutrinos should otherwise be the same, although scattering cross sections and the excitation of an electron into a muon may have radically different cross sections. Second, in addition to the 69-GeV peak in lepton colliders, a 138-GeV peak should also exist, since two A’s could resonantly annihilate into two B’s. This would result in four B’s, which will decay as either four jets, two jets and two leptons, or four leptons. Recent results at LEP may have seen just such a signal.⁽¹⁴⁾ Lastly, production of single C’s at hadron colliders should result in the production of same-sign lepton pairs along with missing energy.

Present dogma may lead one to predict that the vertex diagrams and loops associated with a quantum neutrino dynamics (QND) calculation would violate spin conservation at the vertex. The problem with this prediction is that it assumes that QND must take the same form as quantum electrodynamics (QED). But worse, this prediction assumes that conservation rules must hold at every order in the perturbative expansion series, rather than only holding for the Hamiltonian as a whole. Applying rules that hold for one branch of physics (QED) to another (QND) is not really relevant. What is needed is a new dynamics for QND.

The 69-GeV resonance predicted herein will not affect calculations of experiments done at lower energy. Low-energy experiments are sensitive to the charged and neutral weak currents. In the Standard Model these weak currents correspond to the exchange of a W or a Z, and only one Z (and Z peak) is permitted. In the model proposed here, two "Z-like" peaks are predicted in high-energy experiments, along with the observation of "W-like" events. But the underlying A-B-C model still only uses A and B as the entities that tunnel out during weak decays, with A tunnelling being associated with weak neutral currents and B tunnelling being associated with weak charged currents. There are still only two types of weak decays to influence low-energy experiments, and the masses associated with the tunnelling, twice the mass of the B for weak charged currents and twice the mass of the A for weak neutral currents, are within the error bars originally expected for the discovery of the W and the Z.

It is clear that any physical model should have calculational ability. The model proposed herein is not yet developed to that point. The model merely points out a simple pattern in nature and makes some experimental predictions. The model is about at the state of the initial quark modelling of the eightfold way and the tenfold way. A good dynamical underpinning should be able to account for the problems indicated above. In addition, lepton masses and hadron masses should, in principle, be calculable, as should neutrino interaction cross sections.

It may be that the theoretical machinery is already developed to do these calculations. Supersymmetry is purported to be a theory where each fermion has a boson partner, and each boson has a fermion partner. (In QED the particles are fermions and force carriers bosons. In the theory proposed herein the A, B, C particles may be bosons and the force carrier is a fermion.) Other theories may also exist that can be applied to the model proposed here. (Two excellent review articles, each containing over 500 references, which concern alternatives to the Standard Model, are Nilles⁽¹⁵⁾ and Haber and Kane.⁽¹⁶⁾) Unfortunately, this author is not an expert in those matters. But the development of physical theory often requires the contributions of many. The Standard Model has seen an enormous amount of effort over the years. A similar level of effort may also be required for the model proposed herein, especially in the realm of dynamics.

The model proposed herein has several philosophical advantages over the Standard Model:

(1)The number of elementary particles is vastly reduced. Equations (14), (15), and (17) account for all particles accounted for by the Standard Model, but they do so in a way that involves far fewer "elementary" particles: the 36 quarks and 12 leptons have been replaced by the 6 A-B-Cs.

(2)The underlying forces of nature have been reduced in number from 4 to 3. While electromagnetism and gravitation remain unchanged, it is now proposed that the force responsible for holding together the hadrons and leptons is actually the neutrino-motive force, which replaces the strong force. The weak force is proposed to be the result of quantum tunnelling; it is actually not a force at all. All weak decays can be seen to be examples of such tunnelling. The tunnelling process need not be restricted to the beta decay example of Eq. (12).

(3)An entire quantum number, color, can be set aside, along with its force carriers, the eight gluons.

(4)All observed massive particles of nature, baryons, mesons, and the massive leptons, can be described with a united, rather than a disjointed, set of elementary constitutive particles.

(5)There is a symmetry (possibly supersymmetry) in treatment between atomic physics, which is the science of how nature binds fermions with a force carried by a massless boson, and elementary particle physics, which is here proposed as a science of how nature binds A-B-Cs (which are possibly bosons) with a force carried by a massless fermion.

(6)A clear dichotomy is established between particles, which are all massive, and force carriers, which are all massless.

(7)The existence of the A-B-Cs as "elementary" particles is much clearer than in the case of quarks, since A and B have been shown to be (via W and Z events), and C is predicted to be, experimentally isolatable, while the Standard Model predicts that quarks can never be isolated.

A not-so-Standard Model for elementary particles has been proposed that obtains great improvements in the underlying simplicity of our view of nature over the view held by the Standard Model. The number of elementary particles is reduced from 48 in the Standard Model to 6. The number of forces of nature is reduced from 4 in the Standard Model to 3. A quantum number, color, can be eliminated. Since the massive leptons are constructed by the new elementary particles, and since the labelling of hadrons via quarks can be recovered, the model proposed herein can be used to construct all known massive particles. The existence of new particles, the A, B, and C particles, is postulated, and the underlying model predicts a new phenomenon not predicted by the Standard Model, that is, a 69-GeV "B resonance" should be observable in hadron and lepton colliders.

This work has benefited from numerous discussions with many individuals over the years. The early formation of the not-so-Standard Model was aided by discussions with many of my fellow graduate students at the University of Wisconsin during the years 1982 to 1985: Dan Gee, Gerry Bauer, Mike Procario, and Al Gara all provided useful commentary. Professor Francis Halzen also kindly responded to my questions. In 1994 the model benefited from comments of Narayan Mahale, Fred Gilman, Ted Garavaglia, David Johnson, Ron Schailey, Victor Yarba, Jay Jayakumar, and Ken McFarlane. The help of all the aforementioned has been especially useful in that they do not typically share this author's views. I would also like to thank the anonymous reviewers of Physical Review Letters for their comments, which clarified some of the opposition this model will face. I value the help of François Ostiguy in his translation of the abstract into French. Lastly, I greatly appreciate the efforts of the editor and reviewers of Physics Essays, since these efforts led to the production of an improved version of this work.

Received 22 August 1994.

1. S. Bludman, Nuovo Cimento 9, 433 (1958).

2. S.L. Glashow, Nucl. Phys. 22, 579 (1961).

3. M. Gell–Mann, Phys. Lett. 3, 214 (1964).

4. A. Salam and J.C. Ward, Phys. Lett. 13, 168 (1964).

5. S. Weinberg, Phys. Rev. Lett. 19, 1264 (1967).

6. A. Salam, Proceedings of the 8th Nobel Symposium Stockholm 1968, edited by N. Svartholm (Almqvist and Wiksells, Stockholm, 1968), p. 367.

7. S. Glashow, J. Iliopoulos, and L. Maiani, Phys. Rev. D 2, 1285 (1970).

8. M. Kobayashi and M. Maskawa, Prog. Theor. Phys. 49, 652 (1973).

9. H.D. Politzer, Phys. Rep. 14, 129 (1974).

10. W. Marciano and H. Pagels, Phys. Rep. 36, 137 (1978).

11. G. Arnison et al. (The UA1 Collaboration), Phys. Lett. B 122, 103 (1983).

12. P. Bagnaia et al. (The UA2 Collaboration), Phys. Lett. 129, 130 (1983).

13. F. Halzen and A.D. Martin, Quarks & Leptons: An Introductory Course in Modern Particle Physics (John Wiley & Sons, NY, 1984).

14. G. Taubes (news article), Science 272, 474 (1996).

15. H.P. Nilles, Phys. Rep. 110, 1 (1984).

16. H.E. Haber and G.L. Kane, Phys. Rep. 117, 75 (1985).

Superconducting Super Collider Laboratory^a

MS 1040

2550 Beckleymeade Ave.

Dallas, Texas 75237 U.S.A.