Let us consider a Minkowski 2-dimensional space time, in which there we introduce TWO inertial coordinates, x and t, which, according to relativistic physics, should be considered almost "of the same nature" (we suppose to use geometrical unities, namely that c = 1). An "equation of motion" of a "material point" (or "particle") in M is something of the kind:

x = x(u), t = t(u)

with the requirements that:

1 - the functions involved are "regular" for any value of the real parameter u;

2 - the derivative vector (x'(u),t'(u)) has ds² equal to -1, namely, the following identity x'(u)² - t'(u)² = -1 holds (the parameter u, unique up to translation, is called a proper time of the particle);

3 - this "curve" is "future-pointing", in the given "time-orientation" of M.

Having thus precisely DEFINED what a motion is in Special Relativity, one discovers that the expression (x'(u),t'(u)) is really a 2-vector of M, which is called the 2-velocity of the point. By this we mean that if one does compute this velocity with other different coordinates, then one gets always the same geometrical vector, of which the two numbers (x'(u),t'(u)) are just the coordinates, which are possibly varying from one system to another.

Let us now remark that the first of the aforesaid conditions implies that t'(u) can never vanish, as a matter of fact, it is always a positive quantity:

t'(u)² = 1 + x'(u)². This implies, in force of the well known implicit function theorem, that one can write (first LOCALLY, but then GLOBALLY, since we are in the case of one variable!) the inverse of the function t = t(u) as u = u(t), and then express x as x = x(u) = x(u(t)) = some function of t, say x = f(t).

So the first point which we have reached is that an equation of motion can be expressed in the coordinates (x,t) as an usual classical motion law x = f(t), but its velocity has not an "absolute" meaning in M, only a "relative" one (that is to say, relative to the system (x,t)).

Well, one could say that these are just pedantic mathematical sophistications, with no "physical meaning", but these arguments become important when one asks to pass from a given equation of motion in the simple form x = f(t) in some given coordinate system (x,t) (let us maintain the hypothesis that these are inertial, or Lorentzian, coordinates) to the new equation which does represent the same motion in a new coordinate system (x',t'), connected to (x,t) by the Lorentz equations: x' = (x-vt)g , t' = (t-vx)g , where as usual g = .

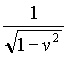Remark. Beware of the fact that the apices in x' and t' do not actually mean derivatives!

As one can immediately see, by means of the equation x = f(t), one gets:

x' = (f(t)-vt)g , t' = (t-vf(t))g , which is not a good representation of the motion which we are aiming for, since in them appears a dependence from the "old" coordinate time, and neither from the "new" coordinate time t', nor from the canonical parameter which satisfies the aforesaid condition:

ds²(derivative vector) = -1.

In other words, the problem is to get from the two previous equations (which, we repeat, are correct, but are not the ones one wishes to find) the new simple equation of the motion in the form x' = g(t') (as a matter of fact, there will appear a new function g of t' different from the old function f of t).

Well, when one computes dt'/dt from the second of the previous equations, then one gets (1-vf'(t))g , which shows that this derivative is always different from zero, AS IT MUST BE, if and only if the product of the two "velocities" v and f'(t) is different from 1, which is indeed one of the requirements of Special Relativity (both the absolute values of v and f'(t) cannot exceed 1, and cannot be both equal to 1; more precisely, the absolute value of v is less than 1, and the absolute value of f'(t) is less or equal to 1)! Since this product is different from zero, then one can write as before the inverse function of t' = (t-vf(t))g , let it be t = h(t') , and then one gets at last:

x' = [f(h(t'))-vh(t')]g = g(t'), as we required.

A good example of this procedure gives the famous formula for the relativistic composition of velocities. Let us start from a simple linear motion's equation of the kind x = wt, whose relative velocity is obviously w, and let us ask which is the velocity of the same motion in the coordinates (x',t'). Well, first of all one gets the equations x' = (wt-vt)g = (w-v)tg , t' = (t-vwt)g = (1-vw)tg , and then one must take the inverse of the second one: t = 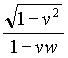t'. One must substitute this value in the first equation, thus getting: x' = (w-v)g 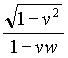t' = 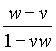t', and from this equation one gets: = 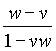, which is indeed the famous formula we wished to obtain (and if w = 1, namely if we have a "photon" travelling in the system (x,t), then we get = = 1, that is a say a photon which is travelling with the same speed 1 in the coordinate system (x',t'), this is in any case good mathematics).