Our aim is to discuss the following "ideal" situation:

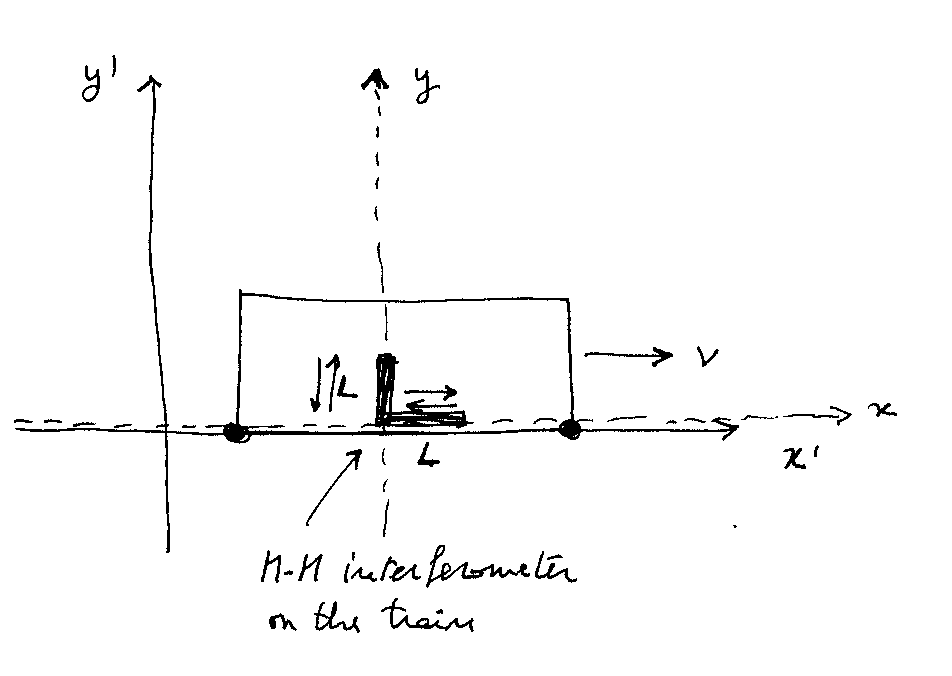
- An "inertial observer" A (this word has a precise geometrical* meaning in Minkowski space-time M) is inside a "train", performing a M-M experiment, in the following simple case:

- another inertial observer A' is "standing" near the railway's track, and he is watching the train - which goes with some uniform speed v > 0 with respect to A' - from outside.

Since we are doing a relativistic discussion, we have obviously supposed that both A and A' are "equipped" with Lorentzian space-time coordinates, (x,y,t) for the first, (x',y',t') for the second, and that the following well known Lorentz transformation does connect the two coordinate systems, let us call them K and K':

x' = (x+vt)g ; y' = y ; t' = (t+b x/c)g ,

(please, remark that we have exchanged the indices with respect to the more familiar set-up) ; in these formulae, as usual: b = v/c , g = 1/sqr(1-b ²) .

When A makes a light's beam b^h goes from left to right, and backwards, "horizontally" in our previous sketch, then b^h comes back to A indeed after a time (which is called a "proper" time, namely a time in the "life" of A):

t^h = t₁ + t₂ = L/c + L/c = 2L/c

(where L is the length of the "travel" of b^h in K , namely the proper length of the interferometer's horizontal arm).

When instead another light's beam b^v , even in some other moment, comes back to A after making a "vertical" travel, up and down, then b^v's travel obviously takes the same time as before:

t^v = t₃ + t₄ = L/c + L/c = 2L/c ,

so we can at last write the identities:

t₁ = t₂ = t₃ = t₄ ; t^h = t^v .

We repeat that this is quite "true" in M if we suppose not only that A is an "inertial observer", as we have said above, but even that A makes use of a GOOD "coordinate system" K , that is to say, of Lorentzian coordinates in M (and so the "measures" of light's speed give always the same result c , either one-way or two-ways - do not forget that we are speaking only "in principle", namely in a THEORETICAL framework).

So far, so good, we would daresay, things appear quite understandable (no contrast at all with "ordinary intuition"), but let us see now how the whole situation would "appear" to A' according with Special Relativity (SR). We start with the simplest case, the vertical travel. When looking at the vertical travel of b^v , then A' sees that b^v follows one "diagonal" path, which is drawn in the following sketch:

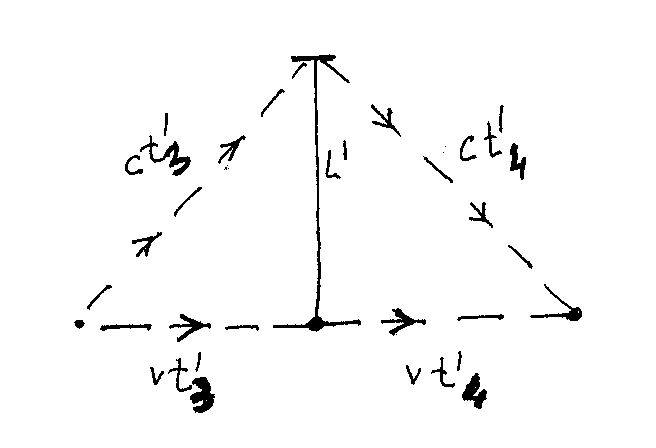
and since b^v travels with the same speed c even with respect to A' (once again according with SR's assumptions: light's speed does not depend from the speed of the light's source), then A' can "measure" - with its analogous GOOD coordinates - the two times t'₃ and t'₄ for the two corresponding parts of light's travel (up and down), by means of the following well known argument.

First of all A' can write:

(ct'₃)² = L'² + (vt'₃)² ,

(remember that v is the scalar velocity - speed - of the "train" with respect to A', while we call now L' the length of the vertical arm of the M-M interferometer RELATIVE TO K'; since in SR BOTH spaces and times are "relative" to the "observers" - or coordinate systems - we must A PRIORI suppose that this value could be different from L).

From the previous identity A' gets:

(c²-v²)t'₃² = L'²

t'₃ = L'/sqr(c²-v²) = g L'/c .

In a quite "symmetrical" way, A' finds:

t'₄ = L'/sqr(c²-v²) = g L'/c ,

and then summing up:

t'₃ = t'₄ ; t'^v = t'₃ + t'₄ = 2g L'/c .

Remark - It is rather curious the fact that the previous "diagonal sketch" appears in all theoretical descriptions of the "expectation" of M-M experiment, even if this must be thought of in principle WITHOUT RELATIVITY. As a matter of fact, the sketch takes into account relativity, since its introduction does suppose that the classical laws of the Optics hold in the Earth's frame - possibly moving in the ether, as the experiment aimed to prove at the time in which was performed - while these laws would instead hold a priori only in a frame at rest in the aether! That is to say, some kind of implicit and wrong assumptions are at the ground of most discussions of this famous experiment, and moreover an hypothesis about the "nature of light" is necessary since the beginning. Waves or photons? For a good analysis of which would have to be a right expectation of the experiment, from a classical wave-theoretical point of view, see M. Mamone Capria & F. Pambianco, "On the Michelson-Morley Experiment", Foundations of Physics, 24, 6, 1994.

In order to know exactly which is this time for A' (and please remark that it is by no means a "proper" time, namely a time in the life of A' , but only a COORDINATE TIME with respect to the coordinate system K' associated to A'), and to compare it with the previous value t^v , we must know which is the value of L' . Well, taking into account - AS WE MUST! - the Lorentz transformation above, we can say that:

L' = L ,

(that is to say, in more "physical" words, there is not "length contraction" for "vertical" lengths), and so in conclusion:

t'^v = 2g L/c = g t^v .

That is to say, a time which is equal to the previous t^v = 2L/c multiplied by the factor g .

The previous one is the famous formula of the TIME DILATION, which expresses a PROPER TIME (a proper time of A's life) by means of a COORDINATE TIME (in general, any coordinate time).

Now we come to the horizontal beam b^h AS SEEN BY A' , or better by K' . We could immediately say that A PRIORI we must expect for this time t'^h the SAME time t'^v we have just computed above. As a matter of fact, this cannot be but so, since we did agree at the beginning that the two light's beams b^v and b^h come back simultaneously to A if they start simultaneously from A, and so A' (K') must obviously "witness" the same thing.

The times of the travels are different in K or in K' , namely when evaluated from the point of view either of A (K) or A' (K'), but if t^v = t^h , as we already know, then it must be even true - we repeat it, A PRIORI, not performing any particular computations - that:

t'^h = t'^v .

But we can immediately PROVE - for the skeptics! - that it is indeed so by analysing the horizontal total time in more detail.

Well, according to A', this time t'^h is equal to the sum of two times t'₁ and t'₂ , corresponding to the two previous times t₁ and t₂ . But let us remark at once that it would be a MISTAKE to expect that in SR, according with the time dilation formula, it "should" then be:

t'₁ = g t₁ ; t'₂ = g t₂ .

As a matter of fact, from these two WRONG identities, we would get indeed

t'^h = t'₁ + t'₂ = g (t₁ + t₂) = g t^h ,

which is the CORRECT identity, but we must find this right formula by using the right procedure.

The time dilation formula CANNOT be applied in this case, since it can be applied only to the case of ONE clock, for instance in our case A's clock, as this clock is "seen" in two different "places" in K' (remember, the coordinate system associated to A'). This is so not only because, AS ALWAYS in this kind of situations, A is in front of A' only ONCE, and then A' must "ask" to his other associated "coordinate" observers what is happening to A's clock when A is far away from A' , but principally because t₁ and t₂ , in the same way as t'₁ and t'₂ (but also t₃, t₄, t'₃, t'₄!), ARE NOT time's values shown in the clock of A , or of A' , or of any other observer (either "standing" in K or in K')! All these values are the result of TIME DIFFERENCES of time values shown by different clocks: t₁ and t₂ are the result of TIME DIFFERENCES measured in K, while t'₁ and t'₂ are the result of TIME DIFFERENCES measured in K' . I say it again, they are not simple values directly shown in only one clock! This has the consequence that we cannot apply the time dilation formula to "corresponding" times, and if we wish to know these values, then we must do a direct computation.

As far as t'₁ is concerned, we can write:

L'' + vt'₁ = ct'₁ ,

where L'' is now the length of the horizontal arm of the Michelson-Morley interferometer we are talking about with respect to K' , a value which could in principle be different both from L and from L' .

From the previous identity we get:

t'₁ = L''/(c-v) ,

while in an obvious "symmetrical" way we get:

t'₂ = L''/(c+v) .

From these identities we get:

t'₁ different from t'₂ ,

t'^h = t'₁ + t'₂ = (L''c+L''v+L''c-L''v)/(c²-v²) = 2g ²L''/c .

As before, we have now to face the question which is the right value for L'' . We meet the famous horizontal "length contraction" formula, which connects in our simple case horizontal space measures in K (the system of A) and horizontal space measures in K'. Once again, this is a consequence of the Lorentz trasformation connecting space-time coordinates in K and in K'. This formula is the well known:

L'' = L/g ,

and it implies that in the actual situation the previous expression of t'^h becomes:

t'^h = 2(g ²L/g )/c = 2g L/c = g t^h = g t^v = t'^v ,

exactly as we said that one HAD TO EXPECT A PRIORI.

We remark once again that the time dilation formula could have been instead immediately applied to the SUM of the two times t'₁ and t'₂, which is a value relative to a time interval shown in A's clock as seen by K' in two different places (but remember that in M there are not "real" times or places, only EVENTS), even if it cannot be applied to the two addenda separately. As a matter of fact, the value:

t'₁ = L/g (c-v) = L/(cg (1-b )) = t₁/g (1-b )

is indeed different from g t₁ (correspondingly, t'₂ is different from g t₂ ).

This gives a complete account of the situation we wished to discuss from a relativistic point of view, and one should indeed appreciate how time dilation and space contraction "combine" together in order to give the expected "logical" result - as always in SR - and how things are perfectly "symmetrical", by interchanging the roles of A and of A' (a M-M interferometer is now in the "ground", and travelling observers in the train watch what is happening in the railway's track).

We shall discuss now a more general case of this situation, namely a M-M interferometer which is again aboard into the train, but with its arms oriented in any direction. However, we wish first to emphasize one CURIOUS feature of this "exercise", which many people seem not to realize. The observer A performs indeed a M-M test, and he finds (at least Einstein says so) that the two light's beams come back simultaneously to him. If A' performs an analogous M-M test, then he must get the same result, in agreement with the so called "relativity's principle", a principle which is perhaps not true in Nature. Do we really have enough experimental information about this "truth", as for instance this physicist recently wrote in a discussion group:

> The principle of relativity asserts that the laws of physics are always the same independent of the speed of the reference frame: the experimental evidence confirming this principle is actually overwhelming, in the sense that in no field has one ever discovered any dependence of the forms of the laws of physics on the velocity of the reference frame.

Comment: First of all, this is not really true, for instance in classical Maxwell electromagnetism (see http://www.dipmat.unipg.it/~bartocci/symm.html); second, not to have ever discovered "any dependence etc." cannot be said an "overwhelming experimental evidence", since human beings until now never really made experiments in different reference frames, moving one with respect to another. So all we have is just indirect evidence, or even theoretical evidence, which could just mean that our actual "theories" are not good enough...

Well, coming back to our discussion, when A' (or better, K'!) watches what A is doing, then he cannot but witness that the test which A has performed has given the result we have just described, even if A' should indeed acknowledge that a M-M test with a moving M-M interferometer CANNOT give the result that the two light's beams come back simultaneously where they started from, exactly for the same reasons we have discussed before: "horizontal" and "vertical" times should in this case be different for A' . How is all this logically possible, and not a contradiction? According to A' , a M-M test IN MOTION does or does not give a "null result"? How is it possible that A , as A' , witness for instance a null result in the train, but A' "knows" that a M-M experiment in the train must not give a null result?

The answer is very simple: this is so because the M-M interferometer of A DOES NOT appear a moving M-M interferometer to A' (K'), since it appears as to have unequal arms! Quite symmetrically, a M-M interferometer of A' does not appear a M-M interferometer to A (K). When A' does see a "good" M-M interferometer WITH EQUAL ARMS in the train, moving with some speed v , then he must foresee, according to his "physical laws" (relativistic "physical laws"), that this interferometer would NOT give a null result. If one imagines an observer A standing still on this instrument, then A himself must agree that the test does not give a null result, but in this case the explanation for A is simple: this is due to the fact that this interferometer is not a good one for him, namely that it does have unequal arms. That is to say it once again, if a M-M interferometer is standing with A and it is really good for A, then it gives indeed a null result, but this instrument is not good for A' , and for this reason it gives a null result which should not be expected instead from the point of view of A by a "good" moving interferometer! We have emphasized this point because many people believe that, according with SR, a M-M test ALWAYS gives a null result with respect to any inertial observer X, either if the interferometer is moving with respect to X or not, but this is quite FALSE!

* We use this specification because we wish to remark that it would be difficult to explain what the word "inertial" would really mean from a "physical" point of view, or how to physically establish behind the shadow of a doubt when any given "real" observer X is inertial or not (or worst, to discuss whether real inertial observers exist or not, and whether and to what extent the fact that an observer is not "totally inertial" - as for instance an observer on Earth's surface - would affect the result of his experiments, and force him to a "correction" of the strict relativistic "previsions"...).