* * * * *

"During October, 1971, four cesium atomic beam clocks were flown on regularly scheduled commercial jet flights around the world twice, once eastward and once westward, to test Einstein's theory of relativity with macroscopic clocks. From the actual flight paths of each trip, the theory predicted that the flyng clocks, compared with reference clocks at the U.S. Naval Observatory, should have lost 40+/-23 nanoseconds during the eastward trip and should have gained 275+/-21 nanoseconds during the westward trip ... Relative to the atomic time scale of the U.S. Naval Observatory, the flying clocks lost 59+/-10 nanoseconds during the eastward trip and gained 273+/-7 nanosecond during the westward trip, where the errors are the corresponding standard deviations. These results provide an unambiguous empirical resolution of the famous clock "paradox" with macroscopic clocks."

J.C. Hafele and R. E. Keating, Science 177, 166 (1972)

Description of experiment

Index

HyperPhysics***** Relativity

Go Back

* * * * *

In 1971, experimenters from the U.S. Naval Observatory undertook an experiment to test time dilation . They made airline flights around the world in both directions, each circuit taking about three days. They carried with them four cesium beam atomic clocks. When they returned and compared their clocks with the clock of the Observatory in Washington, D.C., they had gained about 0.15 microseconds compared to the ground based clock.

Eastward Journey Westward Journey

Predicted

-40 +/- 23 ns + 275 +/- 21 ns

Measured

-59 +/- 10 ns + 273 +/- 7 ns

Quote from original paper

More detail

Index

References

HyperPhysics***** Relativity

Go Back

* * * * *

In October 1971, Hafele and Keating flew cesium beam atomic clocks around the world twice on regularly scheduled commercial airline flights, once to the East and once to the West. In this experiment, both gravitational time dilation and kinematic time dilation are significant - and are in fact of comparable magnitude. Their predicted and measured time dilation effects were as follows:

Predicted: Time difference in ns

Eastward Westward

Gravitational

144 +/- 14 179 +/- 18

Kinematic

-184 +/- 18 96 +/- 10

Net effect

-40 +/- 23 275 +/- 21

Observed:

-59 +/- 10 273 +/- 21

Gravitational calculation

Kinematic calculation

Index

HyperPhysics***** Relativity

Go Back

* * * * *

For small changes in gravitational field associated with changes in altitude above the earth, the approximate time dilation expression is

if a comparison is made between a clock on the Earth's surface and one at height h above the surface. Hafele and Keating predicted a time difference of 144 ns on an eastward flight around the world for which the flight time was 41.2 hours. This corresponds to an average height of 8900 m, a reasonable flight altitude for a commercial airline. The time shift is positive (aging faster) for both eastward and westward flights. The predicted value of 179 ns for the westward flight of 48.6 hours duration corresponds to an average altitude of about 9400 meters.

Index

HyperPhysics***** Relativity

Go Back

* * * * *

If the kinematic time dilation expression

is expanded in a binomial expansion, then for small velocities it becomes

For a point on the equator and an aircraft flying over the equator at speed v, the expression becomes

and for the aircraft

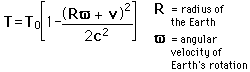
The difference for the airborne clock is then

Application

Index

HyperPhysics***** Relativity

Go Back

* * * * *

For an aircraft flying over the equator, its clocks will show a time shift relative to a fixed surface clock according to the expression

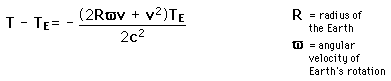
For travel eastward, v has a positive sign and the shift will be negative (aging more slowly). But for a westward flight the time shift is positive (aging faster). Hafele and Keating predicted time shifts of -184 ns for an eastward flight around the world and a shift of +96 for a westward flight.

Index

HyperPhysics***** Relativity

Go Back

* * * * *

RodNave@gsu.edu

Sorry for disturbing, but I had the chance to read your presentation of the Hafele-Keating experiment, and I feel the duty to point out some possible mistakes which appear, in my opinion, in the table "Kinematic Time Shift Calculation". If I am wrong, I would be happy to know your reply.

1 - The first formula, T = T0/sqr(1-v^2/c^2), is intended to give the kinematic time dilation, but it is not made clear what T and T0 mean (as it should be done in a mostly possible self-contained presentation of any argument). The formula would be correct indeed if T0 is a proper time, and T a coordinate time (in the present case, some kind of an "absolute" time, relative to an inertial reference frame in which the Earth does rotate - for instance, a Sun-centered coordinate system).

2 - Formula 2 is surely wrong, or, to say the least, incompatible with the previous formula 1, which would imply a plus sign, instead than a minus. If we want to use formula 2 in the following, it would be better then to EXCHANGE the meaning of the symbols, T is now the proper time, and T0 the "absolute" time, introduced in point 1.

3 - Two expressions follow, giving the dependence of a parameter T from a parameter T0, but in the fifth and last formula, the parameter T0 has suddenly disappeared, while a new parameter TE appears, which has not been before defined, or specified. The only sensible way to give meaning to all this procedure, is:

- write in the third formula TE instead than T, and so this formula would give the correct kinematic time dilation of the proper time measured on the Earth's surface with respect to the aforesaid absolute time T0;

- leave the fourth formula as it is, since it is quite correct, as the formula expressing the same kinematic time dilation of the proper time measured by the aircraft, with respect to the same time T0;

- deduce the fifth formula for the difference T-TE, which is numerically correct, but then replace in the Right Hand Side TE with T0, that is to say, express the difference T-TE in terms of the absolute time of the travel, T0 .

4 - Now I discuss the next Table, Aircraft Time Dilation. Only one formula appears, which is the fifth formula of the previous table, and it should then be corrected, according to my previous remarks, as T-TE as a function of T0. Well, the first assertion after the formula, "For travel eastward, v has a positive sign and the shift will be negative", is correct, but it would be rather misleading with respect to what follows. As a matter of fact, you claim thereafter: "But for a westward flight the time shift is positive", WITH NO PROOF, and then the reader would ask: WHY? At this point, the simplest thing to do for him, is to repeat the previous argument, namely to think: "For travel westward, v has a negative sign...", which is true, but the fact is that from this assumption IT DOES NOT FOLLOW THAT THE WESTWARD TIME SHIFT IS POSITIVE IN ALL CASES! As a matter of fact, the expression -(2Rwv+v^2) [I write w for omega], when v is negative, can be either positive, as you stated, or even negative! It does depend from the sign of the expression 2Rw+v: if this is positive, that is to say, if the absolute value of the eastward speed is LESS than 2Rw (which is the double of the "absolute" Earth's rotation speed - this is perhaps a sensible assumption for an aircraft's speed, a speed relative to the Earth's surface, BUT THE INTRODUCTION OF THIS ADDITIONAL HYPOTHESIS SHOULD BE SPECIFIED), then your conclusion is correct. But for speeds v greater of this value, then EVEN THE WESTWARD (KINEMATIC) TIME SHIFT WOULD BE NEGATIVE!

Thanks for your attention,

Umberto Bartocci

P.S. At the end of the previous point 3, I forgot to point out that, of course, in the discussed fifth formula for the difference T-TE [which I said had to be corrected replacing in the Right Hand Side TE with T0], one could indeed leave in this RHS the Earth's proper time TE, instead than the "absolute time" T0, because, together with the approximation:

TE ~ (1-w^2*R^2/2c^2)T0

one can introduce even its inverse:

T0 ~ (1+w^2*R^2/2c^2)TE ,

which, after substitution of T0, allows to find an approximated expression of T-TE as a function of TE which is exactly identical to the one in which appears T0, and to the one which appears in your table.

That is to say, at this point I indicated just some "imperfection" in the procedure (source of possible misunderstandings for the readers), and NOT a numerical mistake...

Thanks once again for your attention,

Umberto Bartocci