Physics Essays volume 11, number 4, 1998
A Derivation of Maxwell
s Equations from a Simple Two-Component Solid-Mechanical AetherD.J. Larson
Abstract
Maxwell
s equations are derived from a postulated, mechanical,two-component aether.Key words:
Maxwells equations, luminiferous aether, electricity, magnetism, Lorentz, Einsteins special relativity
1. INTRODUCTION
The classical physicists believed that an understanding of nature should enable physical laws to be stated in words as well as mathematics, and that an underlying physical model for the mathematics was crucial to that understanding. Waves were believed to be the result of a substance in motion. In the case of light this required the existence of a new substance, the aether. The purely mechanical approach to physics was altered by Maxwell and others to incorporate a view wherein both mechanical and mathematical models were deemed valuable in our efforts to understand nature. For this reason Maxwell devoted a good portion of his life to the search for a mechanical model that would lead to his famous equations. More recently Mach developed a positivist approach wherein mathematics is all. Relativity abandoned the aether as superfluous.(l) However, due to the persistence of some troubling questions of modern physics (such as the infinities associated with point charges, radiation by point particles, and EPR phenomena(2)), there may be some profit in returning to the classical approach of natural philosophy. If we assign the quantum-mechanical wave-function to the square root of the density of the particle (rather than to a probability of where the particle is), our concept of point particles gives way to one of finitely distributed particles, and the problems associated with point like entities disappear.
Proposing a classical aether and a finite particle size leads to a confrontation with special relativity. It is well appreciated, even celebrated, that relativity correctly predicts experimental results. What is less appreciated is that the predecessor of relativity, Lorentz
s theory of electrons(3) (based on work done by Lorentz, Poincaré, Fitzgerald, and Larmor) equally well predicts the results of experiments.Whether Einstein or Lorentz is correct is still an open question. No experiment has ever been conducted that would indicate that Lorentz was wrong. There is even some experimental evidence supportive of Lorentz over Einstein. Both the two-slit experiment and Aspect et al.
s results(2) of tests of Bells theorem(4) are simple to understand if one views quantum mechanics as a description of real diffuse objects instantaneously collapsing. The nonlocal nature of these experimental results is much more difficult to reconcile with special relativitys insistence on universal point-like interactions and causality only within a light cone.If the Lorentzian classical view of nature is correct, there remains the historical problem of a derivation of Maxwell
s equations from a classical aether. This article presents a very simple, classical, solid-mechanical aether model that is shown to lead to Maxwells equations.2. AXIOMS
This article will assume that F = dp/dt. (Momentum is defined as p = βγmc, where γ = (1 - β2)-1/2, β = v/c, v is the distance traveled per unit time, and c is the speed of light.) For this article, the classical Galilean relativity is also assumed. (Note that Lorentz also assumed Galilean relativity in his derivation of the Lorentz kinematic equations.(3))
This article is meant to serve as a model for an underlying mechanism leading to the classical electrodynamics equations, and therefore does not address quantum-mechanical concerns.
It is assumed that in the absence of sources and waves, a homogeneous, isotropic, solid incompressible aether occupies all space.
From the fact that electrostatics and the theory of atomic dislocations in a uniform solid state lattice are both governed by Poissons equation, it follows that the scalar potential may result from the dislocation of one thing with respect to another. Hence, it is here postulated that the aether is made up of two components. One component is dubbed the firmament, the other component the elasticus.
The postulate of two new substances requires that these substances be named. I have chosen the terms firmament and elasticus to reinforce two notions about the assumed aether. The first name, firmament, comes from the ancient Greek, defined as "the whole vault of the sky". Aether science generally, and the derivation herein particularly, assumes that the aether occupies all space. The second name, elasticus, is herein coined to reinforce the notion of a substance that is solid, and attached with a restoring force to its equilibrium point.
For the model proposed here it will be assumed that in the absence of sources and sinks each small volume of the elasticus is attached to an equally small volume of the firmament. In the theory of condensed matter dislocations the presence of a source (sink) is evidence of some extra (missing) substance disturbing the otherwise homogeneous material. Sources and sinks are therefore proposed to be regions wherein some small volume of firmament has become detached from its counterpart volume of elasticus. As a result of the incompressibility axiom, this detached firmament will push the adjacent attached firmament away from the elasticus to which it is attached. Since the source term in Maxwells use of the Poisson equation is identified as electric charge, detached firmament can now be identified as electric charge. Similarly detached elasticus can be identified as negative electric charge. This model then readily leads to an understanding of the law of electric charge conservation. Whenever a given volume of attached firmament becomes detached (and positive charge is formed), an equal amount of elasticus becomes detached (and an equal amount of negative charge is formed).
From Maxwells equations it is known that a current (flowing charge) acts as a source term. Therefore, flows of detached firmament or elasticus should lead to forces. For the remainder of this work the following simple flow force law is postulated.
Flow Force Law:
When firmament moves with respect to attached firmament (elasticus), a force is generated on the attached firmament (elasticus) that is proportional to the rate of firmament flow, and the direction of the force is in the same (opposite) direction as the flow.A similar law is proposed for the elasticus. When elasticus moves with respect to the attached elasticus (firmament) a force is generated on the attached elasticus (firmament) that is proportional to the rate of elasticus flow, and the direction of the force is in the same (opposite) direction as the flow.
(Note that since the force generated by a moving chargedetached firmamenton the attached elasticus is in the opposite direction as the force generated on the attached firmament, the net reaction force back on the charged particle is zero, and there is no drag force felt by moving charges as they move through the aether.)
We know from experimental evidence that light exhibits transverse polarization. Further, we know that waves in a solid are observed to exhibit transverse polarization, whereas waves in a fluid are not. Nature provides us with many fluidswater and air being the most commonplacebut there are literally thousands of different gases and liquids known to man. These gases and liquids are made up of a vast array of different particles, some with large dipole moments, some not, some spherical, some of vastly distorted shapes. In not a single case do we see transverse polarized waves supported in those fluidic media. Yet solids exhibit such waves all the time. This fact about ordinary materials lends itself to the conclusion that the aether must be a solid. In spite of this fact, many recent authors have proposed aetherial models based on fluidic aethers, with Menos work(5,6) and others referred to therein being examples. While one can never rule out any particular model, and it is possible that the aether is a fluid considerably different than those we now know of, fluidic aether models do have difficulty explaining waves of transverse polarization.
In order to support undamped waves of transverse polarization, the medium must be connected from one small volume to the next. A transverse wave is, after all, a transverse displacement of a portion of the medium with respect to neighboring regions, with that disturbance propagating in a direction perpendicular to that displacement. For this transverse disturbance to be propagated into neighboring regions, a force must exist between the displaced portion and its neighbors. This force is a shear force that can only exist in a solid. Fluids are free to flow in the transverse direction, with no restoring force. There can be a viscous force, but this is frictional and will quickly lead to a damped motion, not an oscillatory one. The viscous force is also proportional to velocity, not displacement, and therefore leads to different physical effects. A small region of water or air moving with respect to its surrounding stationary counterparts sets up graded flows between itself and the nearest stationary boundary condition (the wall). It does not lead to waves of transverse polarization. In order to support light, which is a transversely polarized wave, the aether most likely is in the solid state.
The ideal solid state is a state of utmost simplicity. It can be envisioned either as a continuous block of matter or as atomic in its constituency. In the continuous assumption, a solid is divisible into ever smaller portions, with no change in properties as one goes to smaller and smaller volumes. In the atomic assumption, a solid has a fundamental building block, and is made up of a large number of such building blocks. Mankinds evolution of knowledge of materials in the solid state has evolved to where the atomic view is presently paramount, but many useful investigations were made with the continuous assumption. For the aether proposed herein, the simpler, continuous assumption is all that is required.
Many in todays scientific community might object to the concept of a solid aether. Such a concept is somewhat at odds with what one might assume for a substance in which planets, stars, and elementary particles freely flow. Yet if the laws of nature lead to a condition where elementary particles freely flow through that solid aether, then all bodies will freely flow through the aether, even those as massive as stars.
In dealing with theories of the aether, it is further relevant to note that mankinds experimental data set is quite limited. We perform our experiments on one planet out of nine nearby. The one planet we are on surrounds one star out of billions in one galaxy, and that one galaxy that it is in is again one of billions. And there may be much more that we are unaware of completely. So even though it will be shown herein that the aether locally has the properties of an incompressible two-component solid, it remains quite possible that the aether as a whole is not just a single solid block. It is possible that distant aether has flows and density variations. (Glaciers exhibit flows even though ice is predominantly a solid.) It is possible that in some parts of the universe the aether is no longer solid. (The aether could undergo a phase transition to a fluidic state depending on local conditions.)
Unlimited possibilities exist for those portions of the universe not accessible to our experimentation. All we can do then is to attempt to model that portion of the aether for which we have experimental data. While this data can extend to distant galaxies in the light we receive from them, it is nonetheless possible that the wave disturbance (the light) changes its form during its passage to us. All this article attempts is to model aether that is local, as it is this aether that gives us the laws for electromagnetism in our local laboratories. Conclusions about the form of the aether in the entire universe are not within the bounds of our ability to make local experimental determination, and are well beyond the scope of this article.
It must be the role of theoretical science to propose several different models for nature, and to arrange for definitive tests to determine which model most closely represents nature. Therefore, despite the positive evidence supporting a solid aether propounded herein, other aether models (including the fluidic aether models) must also be seriously considered. Even relativitys absurd ramblings must be given the benefit of scrutiny and test. Only by the experimental testing of all competitors can science advance. In the end, experimental tests can be the only judge of which theory best represents truth.
Waves on a solid string exhibit many of the properties of light. Waves on a string exhibit transverse polarization. The underlying medium, the string, is a solid under tension. For this reason the two aetherial components assumed herein are each proposed to be a solid under tension. The tension is herein postulated to obey the following simple force law.
Tension Force Law:
When a small cube of firmament (elasticus) is deformed, the magnitude of the tension perpendicular to each of any two originally parallel faces is proportional to the separation of those two faces, T = k1L.3. AETHER DISPLACEMENTS
It is postulated above that in the absence of disturbances the aether is homogeneous, isotropic, and incompressible. In this rest condition it is possible to divide the aether into small volume elements (cubes) and label each cube with the coordinates of its center, x = (x, y, z). (Here boldface represents the vector quantity, with normal weight given to scalars.) In general, the volume element can undergo displacement from this equilibrium position. We define f(x, y, z, t) here as the displacement of the attached firmament and e(x, y, z, t) as the displacement of the attached elasticus. (An element of firmament originally at the rest position x is displaced to x + f. An element of the elasticus originally at x is displaced to x + e.)
3.1 Ramifications of Incompressibility
As a first step in analyzing aether motions it is necessary to review the role of incompressibility. Consider a volume element having equilibrium size Δx by Δy by Δz. In its equilibrium state the attached firmament will have a density of ρ0, and the equilibrium amount of firmament in the volume element will be ρ0ΔxΔyΔz. If this same volume element is now distorted so that its size becomes Δx + δx by Δy + δy by Δz + δz, the attached firmament density, ρaf, will become
ρ
af = [ρ0 DxDyDz]/[(Dx + dx)(Dy + dy)(Dz + dz)] » ρ0[ 1 - dx/Dx - dy/Dy - dz/Dz]Now recall that, for a small cube of the firmament, the z-displacement of the xy-face at z is fz(x, y, z, t) and the z-displacement of the xy-face at z +
Δz is fz(x, y, z + Δz, t). Therefore, the amount that the volume element is stretched in the z-direction is δz = fz(x, y, z + Δz, t) - fz(x, y, z, t), and δz/Δz = ¶ fz/¶ z in the limit Δz ® 0. Thus, ρaf = ρo[1 - Ñ × f] for the firmament, and a similar analysis yields ρae = ρo[1 - Ñ × e] for the elasticus. Since the firmament (elasticus) is postulated to be incompressible, the density of the attached firmament (elasticus) plus the density of the detached firmament, ρdf (detached elasticus, ρde) must always remain constant (ρaf + ρdf = ρae + ρde = ρo). Thus,Ñ
× f = (ρo - ρaf)/ρo = ρdf/ρo , Ñ × e = (ρo - ρae)/ρo = ρde/ρo . (1)Any vector field f can be decomposed into its longitudinal (fL) and transverse (fT) components, f = fL + fT, where Ñ ´ fL = 0 and Ñ × fT = 0. This allows fL (and eL) to be expressed as the gradient of a scalar potential:
fL = Ñ Yf and eL = Ñ Ye . (2)
Since Ñ × fT = 0, Ñ × f = Ñ × fL.Combining this with (1) and (2) leaves
Ñ
2Yf = ρdf/ρo (3a)and, similarly,
Ñ
2Ye = ρde/ρo . (3b)3.2 Tension Force Resulting from Firmament Displacements
Consider the tension forces per unit area T present on two parallel faces of a small volume element of the firmament, which result from its displacement. Since it is postulated that the firmament is connected, the direction of the tension force must be along the line joining the center of adjacent cubes. A cube with equilibrium position centered at x = xi + yj + zk is displaced to x + f(x, y, z, t) as discussed in section 3, while a cube originally centered at x¢ = xi + yj + (z+
Dz)k is displaced to x¢ + f(x, y, z+Dz, t). The line joining these two cubes is in the direction D = x¢ + f(x, y, z + Δz, t) - x - f(x, y, z, t) = Δzk + f(x, y, z + Δz, t) - f(x, y, z, t). It will be assumed here that the change in f over the distance Δz is small in comparison with Δz, and that only the first-order terms in a Taylor series expansion of f are important in determining the evolution of f. (It is assumed here that the oscillations of the firmament are small, {f(x, y, z + Δz, t) - f(x, y, z, t)}/Δz << 1). Dividing D by the scalar quantity Δz and taking the limit Δz ® 0 leaves the direction of the tension vector asd = [lim
Δz ® 0](D/Δz) = k + ¶ f/¶ z = k + (¶ fx/¶ z)i + (¶ fy/¶ z)j + (¶ fz/¶ z)k.A unit vector in the direction of d is of course u = d/½ d½ . Now
½
d½ = [(1 + ¶ fz/¶ z)2 + (¶ fy/¶ z)2 + (¶ fx/¶ z)2]1/2 = 1 + ¶ fz/¶ z,where the last equality omits terms higher than first order in small quantities. Thus
u = d/½ d½ = {k + (¶ fx/¶ z)i + (¶ fy/¶ z)j + (¶ fz/¶ z)k
}/{1+¶ fz/¶ z} = k + (¶ fx/¶ z)i + (¶ fy/¶ z)j,where again the last equality is obtained by omitting all terms larger than first order in small quantities. The tension is of course the magnitude of the tension multiplied by a unit vector in the direction of the tension, T = Tu.
Now consider the force on a small cube of firmament. To first order in small quantities the tension on the right xy-face of the cube is
T(x, y, z +
Δz, t) =T(x, y, z + Δz, t){k + (¶ fx(x, y, z + Δz, t)/¶ z)i + (¶ fy(x, y, z + Δz, t)/¶ z)j}.
On the left xy-face,
T(x, y, z, t) =
-T(x, y, z, t){k + (¶ fx(x, y, z, t)/¶ z)i + ¶ fy(x, y, z, t)/¶ z)j}.
The force on a side of the cube is equal to the tension per unit area multiplied by the area of the side (ΔxΔy), so the force on the cube due to the tension on the xy-faces is
F
Txy(x,y,z,t) = ΔxΔyΔz{T0(¶ 2fx/¶ z2)i + T0(¶ 2fy/¶ z2)j + (¶ T/¶ z)k} . (4)In (4) all the derivatives are to be evaluated at the point (x, y, z, t). It is assumed that T(x, y, z +
Δz, t) = T(x, y, z, t) + (¶ T/¶ z)Δz, and the limit Δz ® 0 is again taken. It is assumed that the tension magnitude is generally equal to some constant T0 plus some small variable quantity. Again terms are only kept to the first nonvanishing order in small quantities. It remains to evaluate the last term in (4). The proposed tension force law of Section 2 states that T = k1L, where L is the separation of the two faces and k1 is the arbitrary proportionality constant. If the equilibrium tension magnitude T(f = 0) is T0, this corresponds to the situation where the left xy-face of our chosen cube is at z and the parallel right face is at z + Δz, and the separation of the two faces is Δz. For this equilibrium case T = T0 = k1Δz, which implies k1 = T0/Δz. If f is nonzero, the left face is at z + fz(x, y, z), while the right face is at z + Δz + fz(x, y, z + Δz). For this case the separation of the two parallel faces is Δz + fz(x, y, z + Δz) - fz(x, y, z). In this general caseT = k1[Δz + fz(x, y, z + Δz) - fz(x, y, z)] = T0[Δz + fz(x, y, z + Δz) - fz(x, y, z)]/Δz.
Taking the limit Δz ® 0 leaves T = T0[1 + ¶ fz/¶ z] Þ ¶ T/¶ z = T0¶ 2fz/¶ z2 and this leaves (4) as FTxy(x, y, z, t) = T0ΔxΔyΔz{(¶ 2fx/¶ z2)i + (¶ 2fy/¶ z2)j +(¶ 2fz/¶ z2)k}. Now the force on the cube due to tension on the yz- (xz-) face can be analyzed in an identical fashion by replacing z by x (y) in the above analysis. Summing the forces on all faces, the force on the cube due to displacement-related tension is
FT = T0 ΔxΔyΔzÑ 2f . (5)
3.3 Flow Forces Resulting from Firmament and Elasticus Motion
The flow force law postulates that motion of the elasticus through the firmament results in a force proportional to the flow. There are two ways to realize such a flow. Detached elasticus can flow, with the rate of flow equal to ρde(vde - ¶ f/¶ t), where vde is the velocity of the moving detached elasticus, and ¶ f/¶ t is the velocity of the firmament. (It is the relative velocity that is relevant to the flow of the elasticus through the firmament. If both move with the same velocity there is no flow of one substance through another.) Or the attached elasticus can flow, with the rate of flow equal to (ρo-ρde)(¶ e/¶ t-¶ f/¶ t).
(Note that the total flow of the attached elasticus through a small cube of the firmament actually involves the total derivative de/dt = ¶ e/¶ t + [¶ f/¶ t] × Ñ e, where the velocity of the firmament cube is ¶ f/¶ t. However, it is postulated throughout this work that aethereal oscillations are small:
¶ e/¶ x » ¶ e/¶ y » ¶ e/¶ z » e << 1 .
Thus we have de/dt = ¶ e/¶ t +
ε[¶ f/¶ t], and to the dominant order in ε, ¶ e/¶ t » de/dt. Similarly, the firmament flow terms also involve the total derivative, but again ¶ f/¶ t » df/dt in the dominant order, so only the partial derivatives need to be kept in this analysis.)It is also possible for the detached firmament to flow through the attached firmament with rate of flow proportional to
ρdf(vdf - ¶ f/¶ t). Thus, including the signs specified by the flow force law, and including the fact that the flow is proportional to the volume of the cube, the force due to flows through the cube, FF, isFF = k2ΔxΔyΔz { -ρde(vde - ¶ e/¶ t) - ρ0(¶ e/¶ t - ¶ f/¶ t) + ρdf(vdf - ¶ f/¶ t) } , (6)
where k2 is the arbitrary proportionality constant.
3.4 The Firmament Equation of Motion
It is assumed throughout this work that the displacements of the aether are small: Ñ × e » ε. It will be shown later that light waves are associated with the transverse component of aetherial displacements. (Light waves are derived from the vector potential.) Thus, the transverse displacement of the aether, e (or f), in the case of light is a sine wave, where the maximum displacement is of order ε compared to the wavelength. The maximum velocity of the aether in such a motion is therefore of order ε as compared to c. (The transverse velocity of the medium (ve) divided by the longitudinal velocity of the wave (c) is equal to the distance traveled by the medium in one oscillation (2emax) divided by the distance traveled by the wave crest in one oscillation (λ): v/c = 2emax/l » e.) Therefore, the motion of the attached aether is nonrelativistic, and the equation F = ma can be applied. Assuming that the firmament has a mass per unit volume of μfρo, the mass of the cube is μfρoΔxΔyΔz. Thus, with the forces on the cube given by (5) and (6), we have
F
= ma = μfρoΔxΔyΔz ¶ 2f/¶ t2 = FT + FF == T0
ΔxΔyΔzÑ 2f + k2ΔxΔyΔz { -ρde(vde - ¶ e/¶ t) - ρ0(¶ e/¶ t - ¶ f/¶ t) + ρdf(vdf - ¶ f/¶ t) } ,or
μ
f ρo¶ 2f/¶ t2 = T0Ñ 2f + k2{ -ρde(vde - ¶ e/¶ t) - ρ0(¶ e/¶ t - ¶ f/¶ t) + ρdf(vdf - ¶ f/¶ t) } . (7)Defining c = [T0/
μf ρo]1/2 and choosing k2 = 4πa2To/c leavesÑ 2f - (1/c2)¶ 2f/¶ t2 = (4πa2/c)[ρdevde + ρ0(¶ e/¶ t - ¶ f/¶ t) - ρdfvdf } . (8)
In arriving at (8), the terms
ρde¶ e/¶ t and ρdf¶ f/¶ t have been dropped as they are of second order in small quantities: By (1), ρde << ρ0 and ρdf << ρ0 and, as pointed out above, ¶ e/¶ t = ve » εc.3.5 The Elasticus Equation of Motion
The equation of motion for the elasticus can be derived similarly to the above derivation by replacing f by e, ρdf by ρde, T0 by T0¢ , μf by μe, and vdf by vde. This leaves
(T0¢ /T0)Ñ 2e (μe/μf)(1/c2)¶ 2e/¶ t2 = -(4πa2/c)[ρdevde + ρ0(¶ e/¶ t - ¶ f/¶ t) - ρdfvdf } . (9)
3.6 Maxwell
s EquationsMaking the identifications fL - eL = Ñ ψf - Ñ ψe = -Ñ φ/(4πρ0), J = ρdfvdf - ρdevde, and ρd = ρdf - ρde leaves (8) and (3) as
Ñ 2f - (1/c2)¶ 2f/¶ t2 = -(4πa2/c)J + (a2/c)(¶ /¶ t)Ñ φ + (4πa2ρ0/c)(¶ eT/¶ t - ¶ fT/¶ t) . (10)
and
Ñ
2φ = -4πρd . (11)Equation (10) can be divided into its transverse and longitudinal components:
Ñ 2fT - (1/c2)¶ 2fT/¶ t2 = -(4πa2/c)JT + (4πa2ρ0/c)(¶ eT/¶ t - ¶ fT/¶ t) . (12)
and
Ñ 2fL - (1/c2)¶ 2fL/¶ t2 = -(4πa2/c)JL + (a2/c)(¶ /¶ t)Ñ φ . (13)
Now by the continuity equation, ¶
ρd/¶ t = -Ñ × J = -Ñ × JL. By (11), 4π(¶ ρd/¶ t) = -(¶ /¶ t)Ñ 2φ. Thus, both the scalar and vector products of the gradient operator with the right-hand side of (13) are zero, so the right-hand side can be chosen to be zero by proper choice of JL and JT. Now it can be seen by (8) and (9) that if [T0¢ /T0] = μe/μf = -1, eT and fT satisfy the same equation, eT = fT. In that case, and identifying a2A = eT = fT, (10) becomesÑ 2A - (1/c2)¶ 2A/¶ t2 = -(4π/c)J + (1/c)(¶ /¶ t)Ñ φ . (14)
Since Ñ × fT = 0 and since a2A = fT, we have Ñ × A = 0 in this development. Thus, (11) and (14) are recognized as the Gaussian unit Maxwell
s equations in the Coulomb gauge.4. DISCUSSION
The physical model of the aether proposed here leads to physical models for other quantities as well. It is seen that with the assignment above of a2A = eT = fT, the electromagnetic vector potential is simply proportional to the transverse component of the vectorial displacement of the aether from its equilibrium position. (And, of course, light is simply a mechanical oscillation of the aether.) With the other assignment above of fL - eL = f - e = -Ñ
φ/(4πρo), the gradient of the scalar potential is simply seen to be proportional to the vector separation between the two aether components. The electric field is expressed as E = -(1/c)¶ A/¶ t - Ñ φ. For static fields then the separation of the attached aetherial components, f - e, is proportional to the electric field. Figure 1 shows a pictorial example of the electric field of a cylinder of charge resulting from the mechanical solid aether model proposed here. Note the simple underlying mechanical model for what the electric field "is."As mentioned above, electric charge is physically some amount of detached firmament or elasticus, and electric currents are merely the motion of that detached firmament or elasticus. But note that the displacement current is now identified as a motion of attached firmament or elasticus. This unifies the underlying physical model for these two previously different types of currents. (Both moving charge and the displacement current are simply motions of the firmament or elasticus. Since detached firmament is positive charge and detached elasticus is negative charge, positive currents are flowing firmament, and negative currents are flowing elasticus.)
The model presented here allows for a ready explanation for the absence of magnetic monopoles. The model points to the Coulomb gauge as the gauge that is physically relevant, and in the Coulomb gauge there is a single scalar source term. Electric sources are detached elasticus and firmament; there is no counterpart for magnetic sources.
The requirement of [μe/μf] = -1 means that one component of the aether has negative mass. Here negative mass simply means that if one applies a force to the negative mass component it is accelerated in the direction opposite to the applied force. Whether negative mass attracts or repels positive mass gravitationally is a question not addressed here, but the issue is certainly relevant to large-scale gravitational phenomena, as the massive aether could contribute to the mass density of the universe.
Experimental verification of the theory proposed herein may be possible. In an aether-based theory time dilation results from the motion of bodies through the aether. In the model proposed herein electromagnetic waves are simply motion of the aether. Since motion of a clock through the aether results in time dilation, it should also be true that motion of the aether past the clock will result in time dilation. Thus, if a clock is placed within an oscillating electromagnetic field, time dilation should be evidenced. The magnitude of this effect will be proportional to the magnitude of the aether motion, and it may require large fields (and accompanying nonlinear electromagnetic oscillations) before such an affect is strongly evident, but some small effect might be noticeable by placing an atomic clock in a strong RF cavity field. Eventual control over time dilation would of course be of considerable advantage to mankind.
The scope of this article has been limited to a derivation of Maxwells Equations from a postulated solid aether, and to the direct ramifications of that derivation. There are other questions we should ask about such a solid aether however. Once one has defined a solid aether that results in a model for charges (the detached firmament and elasticus) and fields (which result from displacements of the attached firmament and elasticus), those fields must act back upon the charges to produce accelerations in accordance with the Lorentz force equation. Investigations can also be made into the mass density of the firmament and elasticus, and also into the magnitude of the tension and flow forces existing in the aether. Further studies along these lines should lead to further refinement of the properties of a solid aether, and possibly lead to important new tests of the theory.
Acknowledgment
I wish to thank Samir Dutt, Jay Jayakumar, and Ron Schailey, all of the late SSC laboratory, for their reviews and comments. I also wish to thank Chalmers Sherwin for some clarifying comments. I wish to thank an anonymous conscientious reviewer from Physical Review Letters, who pointed out the absence of a2 in a previous submission of this work. And I wish to thank the editor and anonymous reviewers of Physics Essays for their careful work on this document. The clarity of presentation has definitely been improved by all of the aforementioned.
Lastly I wish to note that an anonymous reviewer has indicated that MacCullagh has done work considering a solid material aether. Unfortunately my effort at obtaining more information about the work of MacCullagh was not successful within the time constraints desired for publication of the work herein, and so a comparison of my work and that of MacCullagh must be postponed. The kind reviewer notes that references to MacCullaghs work can be found in A. Sommerfeld, Lectures on Theoretical Physics, Vol. 2, page 108, and also in E.T. Whittaker, Aether and Electricity, but unfortunately the reviewer did not have a direct reference to MacCullaghs work.
Received 8 July 1997.
Résumé
Les
équations de Maxwell sont dérivées en postulant lexistence dun éther mécanique à deux composantes.
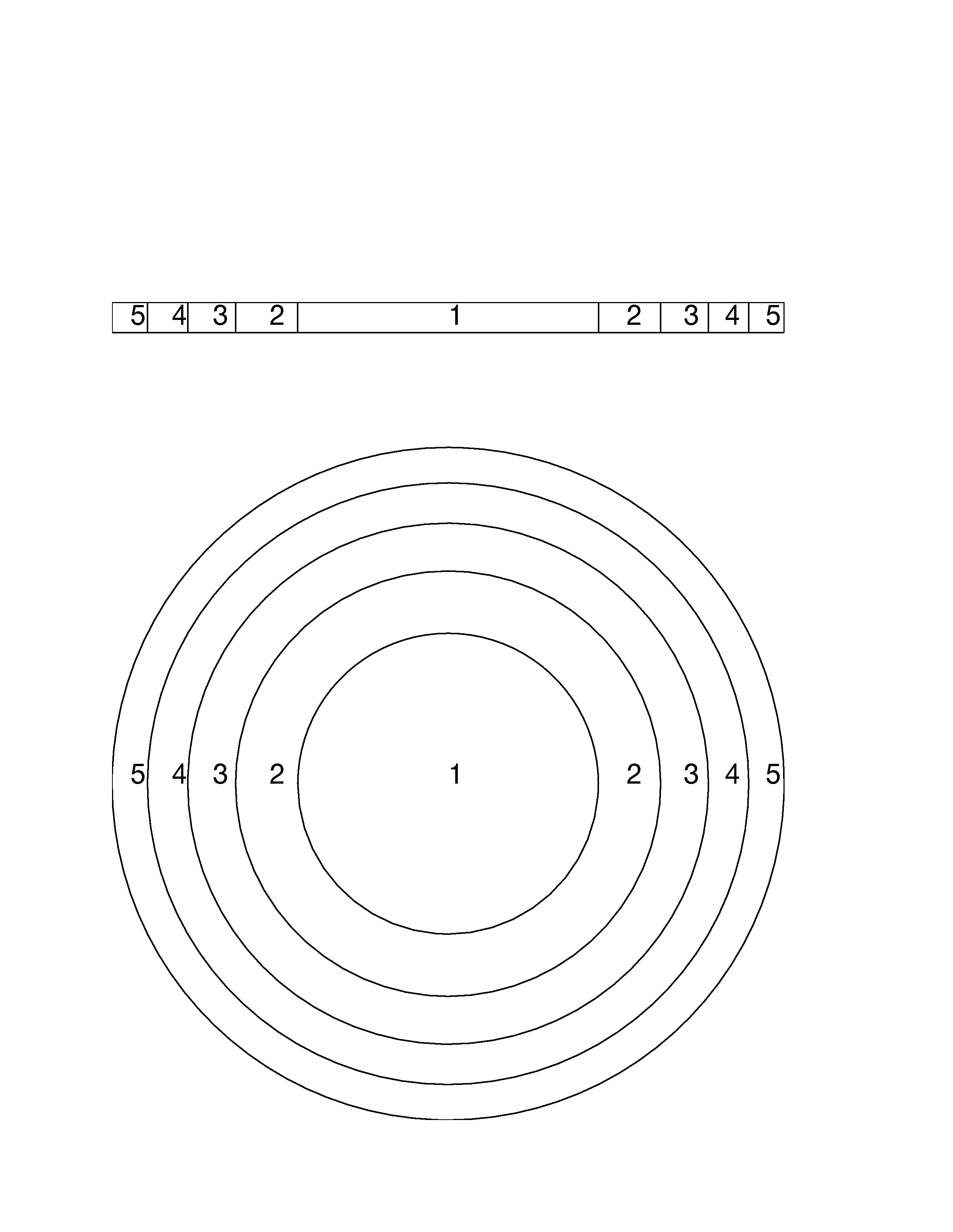
Figure 1. Both the firmament and elasticus can be divided into arbitrary volume elements for analysis. The figure shows the division into infinite concentric cylinders. Bottom: View looking down the symmetry axis. Top: View of a thin slice as seen from a perpendicular angle with respect to the symmetry axis. Case 1: Without any detached elasticus or firmament present the concentric regions will overlap. The firmament of cylinder 1 will occupy the same space as, and be attached to, the elasticus of cylinder 1. Case 2: If a volume of detached firmament occupies the center cylinder, it will push the attached firmament radially outward, due to the incompressibility of the firmament. This leads to a condition where the attached firmament originally occupying cylinder n now occupies cylinder n + 1, but is still attached to the elasticus of the now adjacent cylinder n. Since all cylinders have the same volume, then 2
πrdr = K for each cylinder, where r is the distance between the cylinder and the symmetry axis and dr is the thickness of the cylinder. The separation of adjacent cylinders is thus equal to dr = K/(2πr). The separation of the attached firmament from its attached elasticus therefore drops off as 1/r, and the separation is purely longitudinal (zero curl). The longitudinal component of the separation is shown herein to be proportional to the gradient of the scalar potential. Physically, Case 2 corresponds to an infinitely long cylinder of charge (the detached central firmament), causing a static electric field (the static longitudinal separation of the attached elasticus from its attached firmament), which drops off as 1/r.
End Notes
1
Please note that this work, which is based on classical physics, intends to use the classical definitions of various terms. In the original definition, "time dilation" meant "clock retardation" and the term had nothing to do with the hocus pocus of special relativitys "relative time." Also, in their original definitions, the terms "mankind" and, contextually, "man" were understood to include people of either gender, and that is the intent herein. I regret that in the politics of our time a movement has arisen (political correctness) that makes the latter comment necessary.
D.J. Larson
861 Raintree Lane
DeSoto, Texas 75115 U.S.A.
e-mail: Delbert7@aol.com
References