ovvero, alla ricerca di soluzioni "possibili"...
(Umberto Bartocci* e Maria Cristina Vipera*)

(Umberto Bartocci* e Maria Cristina Vipera*)

I
Fu nel 1773 che il filologo tedesco Gotthold Ephraim Lessing (1729-1781) rinvenne, tra i manoscritti della biblioteca "Herzog August" di Wolfenbüttel, un'edizione dell'Antologia greca, raccolta composta da Metrodoro di Bisanzio, un "grammatico" (la specificazione è importante per quel che segue!) vissuto tra la fine del V e il principio del VI secolo DC, cioè nell'oscuro periodo della storia della scienza che viene comunemente detto "dei commentatori". In essa figurava un epigramma, non contenuto nelle altre edizioni conosciute dell'Antologia, esprimente il celebre problema dei buoi di Archimede, di cui era rimasta la sola eco in poche altre fonti del mondo antico (se ne fa cenno in Gemino, in due passi di Cicerone, e in uno scolio pervenutoci del Carmide di Platone, di mano ed epoca ignote). La provenienza autenticamente archimedea del problema è stata bensì messa in discussione, ma inserito poi tale brevissimo testo nell'edizione delle opere del grande siracusano curata dal matematico danese Johan Ludwig Heiberg (1853-1928; Opera omnia, cum commentariis Eutocii e codice Florentino recensuit, Latine vertit notisque illustravit J. L. Heiberg, Lipsiae, In aedibus B. G. Teubneri, 1880-81), "ad esso è stato impresso come un sigillo di autenticità" (dalla presentazione di Attilio Frajese alle Opere di Archimede pubblicate dalla UTET nel 1974), e sull'aspetto storico della questione tanto basti. [A proposito di "autenticità", si distingua opportunamente tra il testo in sé, che non appare certamente opera di Archimede - come si evince attraverso considerazioni filologiche - e il suo contenuto.]
Dei versi in parola presentiamo il testo originale, seguito
subito dopo dalla traduzione italiana, che appare fedele, riportata da
Gino Loria (Storia delle matematiche - Dall'alba della civiltà
al tramonto del secolo XIX, 3 voll., Torino, 1929-33, riediti in un
unico volume da Cisaplino-Goliardica, 1982).

"Ma il più bello e difficile dei problemi inseriti nella citata collezione (tanto difficile, non solo a risolversi, ma ad intendersi, che fu escluso dai primi editori di essa) è quello che viene attribuito ad Archimede, il quale l'avrebbe inviato al suo fedele amico Eratostene da Cirene. Crediamo stretto obbligo nostro riferirne qui l'enunciato: "Calcola, o amico, il numero dei buoi del Sole, operando con cura, tu che possiedi molta scienza; calcola in quale numero pascolavano un giorno sulle pianure dell'isola sicula Trinacria, distribuiti in quattro gruppi di vario colore: uno di aspetto bianco latteo, il secondo splendente di color nero, il terzo poi di un bruno dorato ed il quarto screziato. In ogni gregge i tori erano in quantità considerevole, distribuiti secondo i rapporti seguenti: ritieni i bianchi come eguali alla metà ed alla terza parte di tutti i neri ed ai bruni; i neri poi eguali alla quarta parte ed alla quinta degli screziati e a tutti i bruni; i restanti screziati considerali poi come eguali alla sesta ed alla settima parte dei tori bianchi e di nuovo a tutti i bruni. Le giovenche invece erano distribuite nei rapporti seguenti: le bianche erano eguali precisamente alla terza e quarta parte di tutto il gregge nero; le nere alla quarta parte insieme alla quinta delle screziate prese assieme ai tori; le screziate erano precisamente eguali alla quinta parte ed alla sesta di tutti gli animali del gregge bruno; le brune poi vennero valutate eguali alla metà della terza parte ed alla settima parte del gregge bianco. Quando, o amico, avrai determinato esattamente quanti erano i buoi del Sole, avrai distinto quanti erano di ciascun colore, non ti si chiamerà certamente ignorante nè inabile nei numeri, però non ti si ascriverà peranco fra i sapienti. Ma ora bada bene a questi altri rapporti fra i buoi del Sole. Quando i tori bianchi mescolavansi ai neri formavano una figura equilatera, le vaste pianure della Trinacria erano allora tutte piene di buoi; invece i bruni e gli screziati costituivano una figura triangolare. Quando avrai trovato tutto questo e l'avrai esposto sotto forma intelligibile e avrai anche trovato il numero totale dei buoi, allora, o amico, va superbo per quanto hai fatto come un vincitore e sta sicuro di venire considerato come ricco di quella scienza"".
II
Ciò premesso, diamo la formulazione precisa del problema così come esso viene generalmente formalizzato (con linguaggio e simbolismo "moderno"). Con A, B, C, D indichiamo il numero dei tori dei rispettivi 4 colori, bianco, nero, fulvo, pezzato. Con a, b, c, d il numero delle giovenche dei rispettivi sopraddetti colori (sicché A+a = totale degli animali costituenti la mandria bianca, etc.).
(Sistema 1, "ortodosso")
A = (![]() +
+![]() )B
+ C
)B
+ C
B = (![]() +
+![]() )D
+ C
)D
+ C
D = (![]() +
+![]() )A
+ C
)A
+ C
a = (![]() +
+![]() )(B+b)
)(B+b)
b = (![]() +
+![]() )(D+d)
)(D+d)
d = (![]() +
+![]() )(C+c)
)(C+c)
c = (![]() +
+![]() )(A+a)
)(A+a)
(abbiamo mantenuto l'ordine con cui le equazioni vengono presentate nel testo originale, sicché quella che sarebbe in realtà la settima nell'ordine alfabetico naturale viene prima della sesta, una circostanza che aumenta l'armonia, la simmetria generale del sistema).
Le ultime due condizioni quadratiche imposte da Archimede (che resteranno invariate nel presente scritto) sono rispettivamente:
A+B = numero quadrato
C+D = numero triangolare = 1+2+...+m = m![]() Û
8(C+D)+1 = quadrato.
Û
8(C+D)+1 = quadrato.
(Entrambe si riducono quindi in definitiva alla richiesta che un certo numero sia un quadrato.)
Soluzione delle prime tre equazioni di 1:
A = 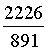 C
= 2226t, B =
C
= 2226t, B = ![]() C = 1602t,
C = 891t, D =
C = 1602t,
C = 891t, D = ![]() C = 1580t
C = 1580t
(t, come poi i parametri u, etc., uguale a 1, 2, 3, ...).
Soluzione del secondo gruppo di quattro, tenuto conto ovviamente delle precedenti:
a = 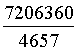 t,
b =
t,
b = 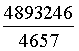 t, c =
t, c = 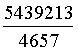 t,
d =
t,
d = 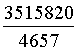 t
t
d'onde infine, posto t = 4657u (4657 è un numero primo):
A = 2226*4657u = 10366482u a = 7206360u
B = 1602*4657u = 7460514u b = 4893246u
C = 891*4657u = 4149387u c = 5439213u
D = 1580*4657u = 7358060u d = 3515820u.
Fin qui niente di male, i numeri in oggetto sono accettabili (ancorché disturbi il fatto che i tori risultano assai più delle giovenche - tutti animali "nobili", che riteniamo distinti da buoi e vacche - una proporzione "innaturale" su cui torneremo), ma le difficoltà cominciano quando si vanno a imporre le ultime due condizioni quadratiche. Infatti:
A+B = 17826996u = 22*3*11*29*4657u = quadrato
implica (quella precedente - e lo stesso sarà nel seguito, quando si tratti di sequenze di moltiplicazioni - è la decomposizione in fattori primi del numero):
u = 3*11*29*4657Y2, ovvero u = 4456749Y2.
Bisogna calcolare adesso C+D = (891+1580)*4657*4456749Y2, e imporre che esso sia un numero triangolare, vale a dire che risulti: 8(C+D)+1 = X2.
Insomma, siamo stati condotti alla cosiddetta equazione di Pell:
X2-8*2471*4657*4456749Y2 = 1, vale a dire:
(1) X2-410286423278424Y2 = 1
che ridotta (eliminando cioè dal coefficiente numerico 410286423278424 i fattori quadrati: 410286423278424 = 23*3*7*11*29*353*46572) diventa:
X2-2*3*7*11*29*353Y2 = 1, ossia:
(1') X2-4729494Y2 = 1.
Dell'equazione precedente vanno ricercate soluzioni (ricordiamo che per i nostri scopi interessa la Y) che siano (appunto nella Y) multiple di 2*4657 (e poi per questo numero 2*4657 = 9314 vanno divise, se si vuole ottenere il valore che realmente ci interessa, da sostituire nella u = 4456749Y2).
Della (1) è oggi possibile, con i moderni strumenti di calcolo elettronico, determinare rapidamente una soluzione fondamentale, che è data da:
e = 109931986732829734979866232821433543901088049+
+50549485234315033074477819735540408986340![]() .
.
La precedente soluzione si determina con il metodo delle
frazioni continue, dopo 92 "passi" (nel senso che il "periodo" di ![]() è 92; si rammenti che la circostanza che tale periodo sia un numero
pari semplifica le cose, nel senso che la soluzione ricercata si trova
presto, senza dover raddoppiare il numero dei convergenti della
frazione continua da prendere in considerazione).
è 92; si rammenti che la circostanza che tale periodo sia un numero
pari semplifica le cose, nel senso che la soluzione ricercata si trova
presto, senza dover raddoppiare il numero dei convergenti della
frazione continua da prendere in considerazione).
[Poiché 4729494 non è congruo a 1 modulo
4, si sa che ZK = Z[![]() ]
è proprio la chiusura integrale dell'anello dei numeri interi
Z nel campo quadratico reale K = Q(
]
è proprio la chiusura integrale dell'anello dei numeri interi
Z nel campo quadratico reale K = Q(![]() )
(Q il campo dei numeri razionali), e inoltre che nel presente caso, periodo
pari, il gruppo delle unità di ZK coincide esattamente
con {
± 1}
´
<e >, a norma del Teorema delle unità
di Dirichlet.]
)
(Q il campo dei numeri razionali), e inoltre che nel presente caso, periodo
pari, il gruppo delle unità di ZK coincide esattamente
con {
± 1}
´
<e >, a norma del Teorema delle unità
di Dirichlet.]
Tutte le altre soluzioni (X,Y) di (1) (intendiamo sempre
X, Y interi positivi) si ottengono elevando la precedente e
= X0+Y0![]() a un esponente intero n (posto: e
n
= X+Y
a un esponente intero n (posto: e
n
= X+Y![]() ), quindi in tal modo
si deve ottenere anche quella che andiamo cercando, "multipla" di 9314
(si sa oggi che essa esiste certamente, ma ai tempi di Archimede c'è
da dubitarne: ogni equazione di Pell, della forma cioè X2-NY2
= 1, dove il coefficiente N è un intero positivo non quadrato, ammette
certamente soluzioni, anzi infinite). Se già avevamo a che fare
con numeri di un certo rispetto, in questa fase della ricerca si va a finire
in numeri addirittura "impossibili" (vedi l'ottima analisi effettuata da
Ilan Vardi:
), quindi in tal modo
si deve ottenere anche quella che andiamo cercando, "multipla" di 9314
(si sa oggi che essa esiste certamente, ma ai tempi di Archimede c'è
da dubitarne: ogni equazione di Pell, della forma cioè X2-NY2
= 1, dove il coefficiente N è un intero positivo non quadrato, ammette
certamente soluzioni, anzi infinite). Se già avevamo a che fare
con numeri di un certo rispetto, in questa fase della ricerca si va a finire
in numeri addirittura "impossibili" (vedi l'ottima analisi effettuata da
Ilan Vardi:
http://www.mcs.drexel.edu/~crorres/Archimedes/Cattle/cattle_vardi.pdf, che dimostra come sia necessario arrivare all'esponente n = 2329). La (minima) soluzione esplicita al problema (ortodosso) di Archimede, che è composta da 206545 cifre decimali, fu calcolata nel 1981 da Harry L. Nelson, usando un supercomputer CRAY 1, e il relativo listato di ben 47 pagine, in formato piccolo, contenente tutte le cifre della soluzione, fu riportato nel Journal of Recreational Mathematics dello stesso anno (Vol. 13, 1980-81, pp. 162-176).
III
E' nostra convinzione però che il problema di Archimede non costituisse solo un "artificio" per convincere eventuali interlocutori di quanto una questione matematica apparentemente semplice possa rivelarsi ben presto del tutto intrattabile, oppure addirittura una beffa giocata ai danni di altri matematici (che è sostanzialmente la tesi contenuta nel libro di Paul Hoffman: Archimede's Revenge: The Joys and Perils of Mathematics, Fawcett Crest, New York, 1988), bensì fosse un autentico problema umanamente risolubile. Tanto più tenuto conto del livello relativamente modesto della scienza aritmetica del tempo, che non pone mai questioni che possano dirsi davvero difficili: si vedano, a mo' di esempio e confronto, i problemi contenuti nei sei (e mezzo) libri superstiti dei tredici originali costituenti l'Aritmetica di Diofanto. Tanto per chiarire meglio questo punto, supponiamo che la soluzione del problema di Archimede non dovesse esigere una maggiore perizia di quella, pur non banale, che richiede la discussione del XXX, e ultimo, problema del V libro dell'Aritmetica, che è riportato anche nella citata Antologia. Ne presentiamo qui, per comodità del lettore, il testo, così come si trova in G. Loria, loc. cit., p. 111, approfittando dell'occasione per segnalare un errore di stampa ivi presente, e per ricordare che il problema in oggetto non ha soluzioni intere, bensì razionali: "Un tale ha comperate [Nell'originale: mescolate.] due qualità di vino, uno a 8 dramme [8, appunto, e non 3.] l'altro a 5 il còngio. Il prezzo pagato è espresso da un quadrato tale che aggiungendovi 60 si ottiene un secondo quadrato avente per lato la somma delle quantità dei due vini. Quanto vino di ciascuna qualità viene acquistato?".
Quindi, pur senza dimenticare che Archimede è l'autore dell'Arenario, e che possedeva manifestamente nozioni relative ai "grandi numeri" (tale osservazione diventerà presto in ogni caso d'attualità), procediamo in questo scritto a esaminare alcune "varianti" del problema, che ammettano, al contrario di 1, soluzioni accettabili. Con tale assunto respingiamo esplicitamente l'ammonimento di Loria (loc. cit.): "nessuno può ardire di affermare [che tale soluzione, quella di cui al paragrafo precedente] superasse le forze di un Archimede". Tali parole rimandano subito la mente al "chi è senza peccato scagli la prima pietra" (Giovanni, 8), ma ci sembra di non pensare male immaginando che in questo caso di pietre ne volerebbero parecchie!
Senza entrare in complesse questioni filologiche, supponiamo cioè che la tradizione del problema, nei secoli che passano dal grande siracusano al pressoché sconosciuto commentatore (probabilmente neppure un esperto di matematica) il quale ce ne riferisce parecchio tempo dopo, abbia corrotto qualche "piccolo" dettaglio, e ne sia risultato modificato pertanto, attraverso un fraintendimento, il testo originale.
L'idea di procedere lungo questa direzione viene da Keith G. Calkins:
http://www.andrews.edu/~calkins/profess/cattle.htm,
il quale, sulla scorta di una traduzione certamente infedele, propone in luogo di 1 il seguente assai interessante sistema:
(Sistema 2, di Calkins)
(A+a) = (![]() +
+![]() )(B+b)
+ (C+c)
)(B+b)
+ (C+c)
(B+b) = (![]() +
+![]() )(D+d)
+ (C+c)
)(D+d)
+ (C+c)
(D+d) = (![]() +
+![]() )(A+a)
+ (C+c)
)(A+a)
+ (C+c)
(le ultime quattro equazioni, e soprattutto le due condizioni quadratiche finali, restano immodificate rispetto al sistema 1).
Soluzione di 2 (un sistema per cui non c'è suddivisione delle 7 equazioni lineari nei due usuali sottogruppi che ne contengono rispettivamente 3 e 4):
A = 12915t, B = 8910t, C = 2020t, D = 12533t
a = 9345t, b = 7110t, c = 6890t, d = 3267t.
Proseguendo:
A+B = 21825t = 32*52*97t = quadrato,
che implica semplicemente:
t = 97Y2.
Facciamo adesso C+D = (2020+12533)*97Y2, e scriviamo nuovamente:
8(C+D)+1 = X2.
Arriviamo all'equazione di Pell:
X2-8*14553*97Y2 = 1, ovvero:
(2) X2-11293128Y2 = 1
che ridotta (11293128 = 23*33*72*11*97) diventa:
X2-2*3*11*97Y2 = 1, ossia:
(2') X2-6402Y2 = 1.
Dell'equazione precedente vanno ricercate soluzioni che siano nella Y multiple di 2*3*7 = 42.
La soluzione fondamentale di (2') è fornita da:
e = 6401+80![]() ,
,
e per raggiungere questo risultato non c'è neanche bisogno di fare ricorso all'espansione di 6402 in frazione continua, la soluzione si può trovare a vista (una circostanza importante, che non si ritrova nelle variazioni che verranno qui successivamente esaminate, e che non viene però messa nella dovuta evidenza da Calkins). Infatti 6402-2 = 6400 risulta un quadrato perfetto (6400 = 802), e si sa quindi che la soluzione minima della (2') è data da:
e = (802+1)+80![]() = 6401+80
= 6401+80![]() ,
,
come si verifica immediatamente (almeno che si tratti di una soluzione, a prescindere cioè dalla sua minimalità; cfr. in generale Waclaw Sierpinski, Elementary Theory of Numbers, Polska Akademia Nauk, Monografie Matematyczne, Warszawa, 1964, pp. 92-93).
La minima soluzione di (2') in cui la Y sia multipla di 42 si ottiene invece elevando il precedente valore e all'esponente 3, ed è precisamente:
e
3 = 1049067577601+(42*312173720)![]() =
=
= 1049067577601+13111296240![]() ,
,
che determina una soluzione davvero accettabile del celebre problema.
IV
Ripetiamo, in verità il sistema 2 conduce a soluzioni che non solo sono enormemente più semplici di quelle dianzi esaminate per 1, ma sono addirittura ottenibili senza effettuare calcoli particolarmente impegnativi, sicché almeno sotto il profilo quantitativo la questione che stiamo affrontando, secondo il punto di vista descritto all'inizio del paragrafo precedente, si potrebbe considerare pienamente, più che soddisfacentemente, risolta. Procediamo soltanto perché può non apparire probabile la corruzione testuale su cui il sistema 2 si basa (nelle righe della pagina di Metrodoro dedicate alle prime tre equazioni del problema di Archimede si parla espressamente di tori), analizzando quindi delle variazioni di 1 nelle quali si mantenga la struttura bipartita del problema (vale a dire, manterremo l'ipotesi che le 7 equazioni lineari siano suddivise in due gruppi omogenei, rispettivamente di 3 e 4 equazioni, le prime 3 non contenendo alcuna delle "ultime" 4 incognite a, b, c, d).
Dopo numerosi tentativi, la prima variazione ragionevole (quindi sotto entrambi gli aspetti dianzi illustrati, quantitativo e testuale) che siamo riusciti a determinare è la seguente:
(Sistema 3, I variazione)
![]() A =
A = ![]() (B
+ C)
(B
+ C)
![]() B =
B = ![]() (D
+ C)
(D
+ C)
![]() D =
D = ![]() (A
+ C)
(A
+ C)
![]() a =
a = ![]() (B+b)
(B+b)
![]() b =
b = ![]() (D+d)
(D+d)
![]() d =
d = ![]() (C+c)
(C+c)
![]() c =
c = ![]() (A+a)
(A+a)
Potremmo dire in termini moderni che si trattava solo di una questione di dove mettere esattamente i coefficienti del sistema lineare, e di parentesi!
Soluzione delle prime tre equazioni di 3:
A = ![]() C
= 58t, B =
C
= 58t, B = ![]() C = 68t, C
= 19t, D =
C = 68t, C
= 19t, D = ![]() C = 66t
C = 66t
mentre la conseguente soluzione del secondo gruppo di quattro è:
a = ![]() t,
b =
t,
b = 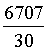 t, c =
t, c = ![]() t,
d =
t,
d = ![]() t
t
d'onde infine, posto t = 120u:
A = 58*120u = 6960u a = 26241u
B = 68*120u = 8160u b = 26828u
C = 19*120u = 2280u c = 28458u
D = 66*120u = 7920u d = 25615u.
(Si noti che, in relazione a quanto abbiamo in precedenza osservato, il rapporto tra tori e giovenche appare attualmente più verosimile.)
Proseguendo:
A+B = 15120u = 24*33*5*7u = quadrato,
che implica:
u = 3*5*7Y2, ovvero u = 105Y2.
Facciamo adesso C+D = (2280+7920)*105Y2 = 10200*105Y2 e scriviamo:
8(C+D)+1 = X2.
Arriviamo all'equazione di Pell:
X2-8*10200*105Y2 = 1, ovvero
(3) X2-8568000Y2 = 1,
che ridotta (8568000 = 26*32*53*7*17) diventa
X2-5*7*17Y2 = 1, ovvero
(3') X2-595Y2 = 1.
Dell'equazione precedente vanno ricercate soluzioni che siano nella Y multiple di 8*3*5 = 120.
La soluzione fondamentale di (3') si ottiene facilmente
con il metodo delle frazioni continue (ancora una volta, 595 è incongruo
a 1 modulo 4, e il periodo di ![]() è pari, precisamente uguale a 10), ed è:
è pari, precisamente uguale a 10), ed è:
e = 18514+759![]() .
.
L'ulteriore analisi volta a determinare una potenza di e tale che il fattore che moltiplica la radice sia un multiplo di 120 si arresta rapidamente a e 20, fornendo la seguente espressione per il numero ricercato:
481190025423905756973520206267276057499295974842445708975828671328250927516594124270524520,
mentre la Y che ci interessa sarà uguale a tale numero diviso per 120, e quindi:
4009916878532547974779335052227300479160799790353714241465238927735424395971617702254371.
Si tratta di un numero evidentemente grande, di 88 cifre, tanto più poi che il valore definitivo, che coinvolge il parametro u, deve contemplare un termine 105Y2, ma si tratta comunque di una soluzione decisamente più presentabile di quella del sistema 1.
V
Il sistema 3 può ammettersi ancora in effetti alquanto complicato sotto l'aspetto quantitativo, e ne offriamo allora una sotto-variazione (sempre "testualmente sensata", in quanto nell'originale pervenutoci, relativamente al secondo gruppo di equazioni, si parla espressamente di tori soltanto quando si danno le informazioni sul numero delle giovenche nere), al di sotto della cui "semplicità" non sembra proprio possibile andare, almeno volendo rispettare il più possibile, come abbiamo detto, la forma bipartita del problema originario.
(Sistema 3', I variazione semplificata)
![]() A =
A = ![]() (B
+ C)
(B
+ C)
![]() B =
B = ![]() (D
+ C)
(D
+ C)
![]() D =
D = ![]() (A
+ C)
(A
+ C)
![]() a =
a = ![]() b
b
![]() b =
b = ![]() (D+d)
(D+d)
![]() d =
d = ![]() c
c
![]() c =
c = ![]() a
a
La soluzione delle prime tre equazioni di 4 è la stessa di prima:
A = ![]() C
= 58t, B =
C
= 58t, B = ![]() C = 68t, C
= 19t, D =
C = 68t, C
= 19t, D = ![]() C = 66t
C = 66t
mentre la soluzione del secondo gruppo di quattro è:
a = ![]() D,
b =
D,
b = ![]() D, c =
D, c = ![]() D,
d =
D,
d = ![]() D,
D,
d'onde infine:
a = ![]() *33t,
b =
*33t,
b = ![]() *33t, c =
*33t, c = ![]() *33t,
d =
*33t,
d = ![]() *33t.
*33t.
Le equazioni parametriche così determinate mostrano che è adesso sufficiente porre t = 10u, sostituzione che fornisce quindi il seguente complesso assai semplice di soluzioni:
A = 580u a = 693u
B = 680u b = 924u
C = 190u c = 594u
D = 660u d = 495u.
Proseguendo:
A+B = 1260u = 35*36u = 22*32*5*7u = quadrato,
che implica
u = 5*7Y2, ovvero u = 35Y2.
Facciamo adesso C+D = 850*35Y2, e scriviamo
8*850*35Y2+1 = X2.
Arriviamo all'equazione di Pell:
(4) X2-238000Y2 = 1
che ridotta diventa ancora ovviamente (238000 = 202*595):
(4') X2-595Y2 = 1.
Abbiamo già a disposizione la soluzione fondamentale dell'equazione precedente, ma adesso vanno ricercate soluzioni che siano nella Y soltanto multiple di 20, per il che si vede facilmente basta arrivare a e 10.
Forniamo esplicitamente tale soluzione (che, rammentiamo, va poi divisa per 20, al fine di individuare il numero Y che veramente ci interessa):
99314822072357424638629318873485084304777260 =
= 20*4965741103617871231931465943674254215238863.
Il numero che moltiplica il 20 nel secondo membro della precedente identità si esprime con "sole" 43 cifre, e fornisce infine la richiesta soluzione al problema di Archimede quando lo si elevi al quadrato, e lo si moltiplichi poi per il fattore 35. Si tratta del numero (di 87 cifre):
863050464785601181421794626162052648276832343542246409279779840754854754796025093646915,
il quale, moltiplicato da ultimo per i coefficienti 580, 680, ... dianzi elencati, fornisce finalmente la soluzione richiesta. Questa ci sembra la risposta più piccola possibile allo storico enigma, e in qualche misura confacente alla personalità e al genio dell'autore dell'Arenario.
[E' forse interessante osservare esplicitamente come si
possa arrivare a determinare gli esponenti ricercati utilizzando semplici
elementi della teoria delle congruenze. Spieghiamo la questione utilizzando
per brevità il linguaggio moderno dell'algebra. Assegnati, come
nel caso in esame, l'anello R = Z[![]() ]
e l'elemento e = 18514+759
]
e l'elemento e = 18514+759![]() ,
volendo ricercare potenze di e la cui seconda
componente Y sia multipla di 4, si introduca l'anello R' = Z4[x
] = { x+yx
}
(ove palesemente x, y sono elementi di Z4, e x
2
= classe di 595 modulo 4 = 3), il quale risulta immagine omomorfa naturale
di R tramite la corrispondenza:
,
volendo ricercare potenze di e la cui seconda
componente Y sia multipla di 4, si introduca l'anello R' = Z4[x
] = { x+yx
}
(ove palesemente x, y sono elementi di Z4, e x
2
= classe di 595 modulo 4 = 3), il quale risulta immagine omomorfa naturale
di R tramite la corrispondenza:
f: X+Y![]() ®
x+ yx , x = classe di X modulo 4, y = classe
di Y modulo 4. Si osservi che, manifestamente, allo stesso modo che Z[
®
x+ yx , x = classe di X modulo 4, y = classe
di Y modulo 4. Si osservi che, manifestamente, allo stesso modo che Z[![]() ]
è isomorfo all'anello dei polinomi Z[x] modulo l'ideale principale
generato da x2-595, così Z4[x
] è isomorfo all'anello Z[x] modulo l'ideale generato da 4 e dal
polinomio x2-595. Ciò premesso, risulta f(e
) = 2+3x , e questo risulta un elemento invertibile
nell'anello R' di periodo 4, tale cioè che esattamente f(e
)4 = 1 Î R', e 4 è il
minimo esponente per cui ciò accade. Tale circostanza significa
appunto che la seconda componente di e
4
è divisibile per 4, ma per pervenire a questa desiderata conclusione
basterebbe considerare, come dianzi implicitamente asserito, la seconda
potenza di e , dal momento che f(e
)2 = -1. Lo stesso ragionamento si può applicare a congruenze
modulo 5, in modo da arrivare infine all'esponente 2*5 = 10.]
]
è isomorfo all'anello dei polinomi Z[x] modulo l'ideale principale
generato da x2-595, così Z4[x
] è isomorfo all'anello Z[x] modulo l'ideale generato da 4 e dal
polinomio x2-595. Ciò premesso, risulta f(e
) = 2+3x , e questo risulta un elemento invertibile
nell'anello R' di periodo 4, tale cioè che esattamente f(e
)4 = 1 Î R', e 4 è il
minimo esponente per cui ciò accade. Tale circostanza significa
appunto che la seconda componente di e
4
è divisibile per 4, ma per pervenire a questa desiderata conclusione
basterebbe considerare, come dianzi implicitamente asserito, la seconda
potenza di e , dal momento che f(e
)2 = -1. Lo stesso ragionamento si può applicare a congruenze
modulo 5, in modo da arrivare infine all'esponente 2*5 = 10.]
VI
Esaminiamo ora altre due possibili variazioni, strettamente conformi alla linea di pensiero precedentemente seguita, anche se si riveleranno meno interessanti delle due precedenti, e a maggior ragione quindi di quella di Calkins. Mantenendo pertanto la struttura bipartita del problema, e allo scopo di considerare nelle prime tre equazioni le rispettive coppie di incognite B,C; D,C; A,C; separate come nel sistema ortodosso 1, poniamo:
(Sistema 4, II variazione)
![]() A =
A = ![]() B
+ C
B
+ C
![]() B =
B = ![]() D
+ C
D
+ C
![]() D =
D = ![]() A
+ C
A
+ C
![]() a =
a = ![]() (B+b)
(B+b)
![]() b =
b = ![]() (D+d)
(D+d)
![]() d =
d = ![]() (C+c)
(C+c)
![]() c =
c = ![]() (A+a)
(A+a)
Prima di andare avanti, notiamo esplicitamente che non
sarebbe possibile scrivere, in analogia formale rispetto alle prime tre,
le ultime quattro equazioni come ![]() a
=
a
= ![]() B+b, etc., perché
il sistema che ne conseguirebbe non avrebbe soluzioni. Invece è
possibile prendere in considerazione la seguente sotto-variazione semplificata
del sistema 4:
B+b, etc., perché
il sistema che ne conseguirebbe non avrebbe soluzioni. Invece è
possibile prendere in considerazione la seguente sotto-variazione semplificata
del sistema 4:
(Sistema 4', II variazione semplificata)
prime tre equazioni identiche a 4
![]() a =
a = ![]() b
b
![]() b =
b = ![]() (D+d)
(D+d)
![]() d =
d = ![]() c
c
![]() c =
c = ![]() a
a
Bene, indaghiamo adesso le soluzione di 4, e della sua forma semplificata 4'.
Soluzione delle prime tre equazioni di 4:
A = 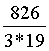 C
= 826t, B =
C
= 826t, B = ![]() C = 1068t,
C = 57t, D =
C = 1068t,
C = 57t, D = ![]() C = 1050t
C = 1050t
mentre la conseguente soluzione del secondo gruppo di quattro è:
a = 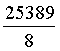 t,
b =
t,
b = 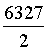 t, c =
t, c = 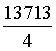 t,
d =
t,
d = 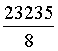 t,
t,
d'onde infine, ponendo t = 8u:
A = 826*8u = 6608u a = 25389u
B = 1068*8u = 8544u b = 25308u
C = 57*8u = 456u c = 27426u
D = 1050*8u = 8400u d = 23235u.
Proseguendo, come ormai familiare:
A+B = 15152u = 24*947u = quadrato,
e ciò implica:
u = 947Y2.
Facciamo adesso C+D = 8856u = 8856*947Y2, e scriviamo come al solito:
8(C+D)+1 = X2.
Arriviamo all'equazione di Pell:
X2-8*8856*947Y2 = 1, ovvero:
(5) X2-67093056Y2 = 1
che ridotta diventa (67093056 = 26*33*41*947):
X2-3*41*947Y2 = 1, ovvero:
(5') X2-116481Y2 = 1.
Dell'equazione precedente vanno ricercate soluzioni che siano nella Y multiple di 8*3 = 24.
La soluzione fondamentale di (5') si ottiene dopo 32 passi (si noti che questa volta siamo nel caso di un coefficiente congruo a 1 modulo 4, quindi quella che segue non è l'unità fondamentale della chiusura integrale di Z nella relativa estensione quadratica del campo dei numeri razionali), ed è:
e = 960014391070295+2812873477652![]() .
.
Una soluzione la cui seconda componente sia multipla di 24 si trova elevando la precedente soluzione fondamentale alla sesta potenza, ed è chiaro che siamo in un caso peggiore di quello discusso con il coefficiente 595.
Passando alla sotto-variazione 4', la soluzione delle prime tre equazioni è ancora:
A = 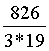 C
= 826t, B =
C
= 826t, B = ![]() C = 1068t,
C = 57t, D =
C = 1068t,
C = 57t, D = ![]() C = 1050t
C = 1050t
mentre la soluzione del secondo gruppo di quattro è, come già visto:
a = ![]() D,
b =
D,
b = ![]() D, c =
D, c = ![]() D,
d =
D,
d = ![]() D,
D,
dal che si trae:
a = ![]() 105t,
b = 14*105t, c = 9*105t, d =
105t,
b = 14*105t, c = 9*105t, d = ![]() 525t,
525t,
d'onde infine, posto semplicemente t = 2u:
A = 826*2u = 1652u a = 2205u
B = 1068*2u = 2136u b = 2940u
C = 57*2u = 114u c = 1890u
D = 1050*2u = 2100u d = 1575u.
Proseguendo:
A+B = 3788u = 4*947u = quadrato,
che implica:
u = 947Y2.
Facciamo adesso C+D = 2214*947Y2, e scriviamo ancora una volta:
8(C+D)+1 = X2.
Arriviamo all'equazione di Pell:
X2-8*2214*947Y2 = 1, ossia:
(6) X2-16773264Y2 = 1,
che ridotta (16773264 = 24*33*41*947) diventa:
X2-3*41*947Y2 = 1, vale a dire (ovviamente si ottiene di nuovo (5')):
(6') X2-116481Y2 = 1.
Della (6') = (5') vanno ricercate adesso soluzioni che siano nella Y multiple di 4*3 = 12, anziché 24 come prima. Già nota la soluzione fondamentale e , basta attualmente considerare la sua terza potenza, ma nonostante tale riduzione restiamo ancora in una situazione quantitativamente più complicata di quella relativa al coefficiente 595.
VII
In conclusione, il "gioco" potrebbe in qualche misura
continuare, anche se non sembra del tutto agevole trovare altre strade
che concilino, come abbiamo cercato di fare, l'aspetto quantitativo con
quello testuale, ma fermiamoci qui**. La cosa importante che ci sembra
di aver "dimostrato" è che - ammesso che Archimede, o altri circoli
pitagorici, tramandassero al loro interno le conoscenze indispensabili
per risolvere problemi misti lineare-quadratici del tipo esaminato - si
può ragionevolmente ritenere che tali capacità venissero
applicate a uno dei sistemi modificati dianzi discussi, ma verosimilmente
non
al sistema "ortodosso" 1. Per quanto riguarda l'effettiva possibilità
di raggiungere certe conclusioni al tempo di Archimede, a mano e con metodi
in generale "elementari" (sintetizziamo: qualche conoscenza relativa alle
approssimazioni originate dallo sviluppo in frazione continua di un irrazionale
quadratico, ammissibili tenuto conto che esse si basano sull'algoritmo
euclideo delle divisioni successive, e di quanto esposto nel Libro X degli
Elementi
del grande geometra alessandrino; scoperta del modo di generare diverse
soluzioni di un'equazione di Pell a partire da una data, in termini moderni,
osservazione della moltiplicatività della norma; infine,
considerazioni piuttosto elementari sulla teoria delle congruenze), ma
soprattutto la funzione di "purificazione spirituale" che secondo alcuni
studiosi la pratica con certi algoritmi sarebbe stata ritenuta possedere
presso i circoli neo-pitagorici, rimandiamo ai saggi di Arturo Reghini,
in particolare: Per la restituzione della geometria pitagorica e dei
numeri pitagorici alla loro forma primitiva" (Atanòr, Roma,
1978), La tradizione pitagorica massonica (ristampa, Fratelli Melita,
Genova, 1988), ma soprattutto i ben 7 volumi della sua opera matematica
inedita (i primi due dedicati specificamente all'analisi indeterminata
di II grado), che verrà presentata su Episteme N. 9 (settembre
2004, http://www.robotics.it/episteme).
** Altre varianti da noi esaminate, tutte "peggiori" di
quelle sopra discusse, contemplavano per esempio, in ordine alle prime
tre equazioni, configurazioni del tipo:
A = ![]() B+
B+![]() C
C
B = ![]() D+
D+![]() C
C
D = ![]() A+
A+![]() C
C
una "separazione" delle frazioni elementari che si potrebbe introdurre anche per il secondo gruppo di 4 equazioni, etc..
- - - - -
Breve bibliografia supplementare
- Estremamente interessante per tutto ciò che concerne
Archimede, presente problema compreso, è la Archimedes Home Page
contenuta nel sito del Prof. Chris Rorres: http://www.mcs.drexel.edu/~crorres/Archimedes/contents.html,
dalla quale abbiamo ripreso l'immagine d'esordio.
- Un'interessante ipotesi su come potrebbe essere stato
possibile risolvere una siffatta questione con metodi "elementari" viene
esposta da Antti Nygrén in "A simple solution to Archimedes' cattle
problem", reperibile on line all'URL:
http://herkules.oulu.fi/isbn9514259327/.
- Informazioni generali sulle frazioni continue, le equazioni di Pell, e quella "di Archimede" in particolare, si possono trovare nelle pagine del Blog Matematico di Umberto Cerruti, http://alpha01.dm.unito.it/personalpages/cerruti/.
- Nelle pagine della Galleria Matematica Italiana,
all'URL:
www.mat.uniroma2.it/txt/conf/arch/1997/ galleria/nov97/archimede/buoi.html,
si trova un'ulteriore esposizione del celebre problema,
assieme all'immagine contenente la versione originale dianzi riprodotta.
- In http://www.veling.nl/anne/templars/Statement.html si spiega come un possibile "precursore" del problema di Archimede sia lo stesso Omero (Odissea, Libro XII).
- Giuseppe Scarpati, "La vendetta di Archimede", in:
http://www.123point.net/001topzine/scienze/artsci12.htm.
- - - - -
Ringraziamenti - Gli autori ringraziano sentitamente per la preziosa collaborazione loro prestata durante la stesura della presente nota: il Prof. Daniel Coray, dell'Università di Ginevra; il Dott. Stefano Loretoni (che con la sua passione è stato all'origine di un rinnovato interesse, e si auspica anche del recupero, nei confronti dell'opera matematica inedita del Reghini; sua è la citata presentazione che comparirà su Episteme N. 8); il Dott. Arcangelo Papi, fonte di numerosi stimoli intellettuali a procedere con il presente lavoro, e apportatore di molte significative osservazioni con la sua ragguardevole cultura umanistica, ma non solo.
- - - - -
* Dipartimento di Matematica
Università degli Studi - Perugia
Maggio, 2004